Две линии в треугольнике (4 видео) | Курс школьной геометрии

Две линии в треугольнике

Ключевые слова: основные линии треугольника, медиана, биссектриса, высота, средния линия, серединные перпендикуляры

Рассмотрим произвольный треугольник ABC:

a, b, c — стороны треугольника

$$m_a$$ — медиана к стороне a угла A

$$h_a$$ — высота к стороне a угла A

$$l_a$$ — биссектриса к стороне a угла A

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам.
Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон
Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.

Свойства серединных перпендикуляров треугольника

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

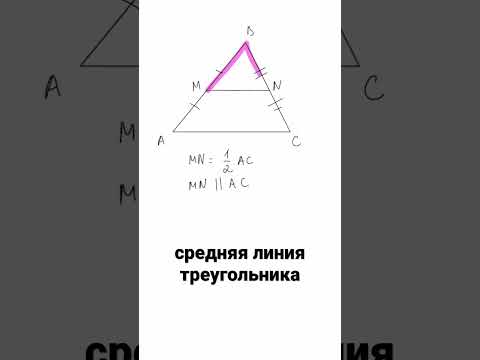
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Содержание

Треугольник. Основные линии треугольника.
Как провести две линии в треугольнике что бы получилось два треугольника и один четырехугольник?
Провести внутри прямоугольника две линии, чтобы получилось пять четырехугольников?
Пожалуйста помогите на фото изображена фигура какие две линии надо провести так чтобы получилось 2 треугольника и 6 четырехугольников?
Начертить четырехугольник и провести в нем две прямых, что бы получилось восемь треугольников помогите пожалуйста?
В четырехугольнике провести два отрезка, чтобы получилось 3 треугольника и 3 четырехугольника?
Как разрезать произвольный треугольник, чтобы получилось 2 треугольника, четырехугольник и пятиугольник, проведя только две линии?
Как провести в прямоугольнике две линии, чтобы получилось восемь треугольника?
Как провести 2 линии чтобы получилось 3 треугольника и 3 четырехугольника?
Провести в фигуре 2 линии чтобы получилось 2 треугольника и 6 четырехугольников?
Еще , в четырехугольнике провести два отрезка так, чтобы получились три треугольника и три четырехугольника?
Как провести 2 отрезка в треугольнике, что — бы получить два треугольника, один четырехугольник?
🎦 Видео

Видео:Средняя линия треугольникаСкачать

Треугольник. Основные линии треугольника.

Треугольник — геометрическая фигура, сформированная тремя отрезками, которые объединяют три точки, не принадлежащие одной прямой. Три точки именуют вершинами треугольника, а отрезки – сторонами треугольника. Стороны треугольника формируют в вершинах треугольника соответственно три угла.

Когда называют треугольник, то указывают три заглавные буквы, стоящие при его вершинах. Для упрощения вместо термина «треугольник» применяют символом /. Треугольник, представленный ниже, указываем как / АВС:

Сторону треугольника общепринято называть одинаковой буквой с вершиной угла, противолежащего этой стороне, но используют при этом малую букву.

Так сторона ВС отмечена буквой а, поскольку она расположена напротив угла А; сторона СА отмечена буквой b, поскольку она расположена напротив угла В; сторона АВ отмечена буквой с, поскольку она лежит напротив угла С.

У треугольник выделяют три угла.

Угол — угол, сформированный сторонами АВ и АС, противолежащий стороне ВС;

Угол — угол, сформированный сторонами АВ и ВС, противолежащий стороне АС;

Угол — угол, сформированный сторонами ВС и АС, противолежащий стороне АВ.

Если продолжим какую-нибудь сторону треугольника, то получим угол, смежный с одним из внутренних углов треугольника. Такой угол называется внешним углом треугольника.

При каждой вершине треугольника может быть построено по два внешних угла:

Видео:Эксперт (Короткометражка, Русский дубляж)Скачать

Как провести две линии в треугольнике что бы получилось два треугольника и один четырехугольник?

Математика | 1 — 4 классы

Как провести две линии в треугольнике что бы получилось два треугольника и один четырехугольник.

Найди середину на каждой стороне и от середины боковых сторон проведи две линии к середине основания.

Получится 2 треугольника и 1 четырехугольник (но не квадрат и не прямоугольник).

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Провести внутри прямоугольника две линии, чтобы получилось пять четырехугольников?

Провести внутри прямоугольника две линии, чтобы получилось пять четырехугольников.

Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

Пожалуйста помогите на фото изображена фигура какие две линии надо провести так чтобы получилось 2 треугольника и 6 четырехугольников?

Пожалуйста помогите на фото изображена фигура какие две линии надо провести так чтобы получилось 2 треугольника и 6 четырехугольников.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Начертить четырехугольник и провести в нем две прямых, что бы получилось восемь треугольников помогите пожалуйста?

Начертить четырехугольник и провести в нем две прямых, что бы получилось восемь треугольников помогите пожалуйста.

Видео:8 класс, 25 урок, Средняя линия треугольникаСкачать

В четырехугольнике провести два отрезка, чтобы получилось 3 треугольника и 3 четырехугольника?

Видео:Геометрия. Линии в треугольникеСкачать

Как разрезать произвольный треугольник, чтобы получилось 2 треугольника, четырехугольник и пятиугольник, проведя только две линии?

Как разрезать произвольный треугольник, чтобы получилось 2 треугольника, четырехугольник и пятиугольник, проведя только две линии.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Как провести в прямоугольнике две линии, чтобы получилось восемь треугольника?

Как провести в прямоугольнике две линии, чтобы получилось восемь треугольника.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Как провести 2 линии чтобы получилось 3 треугольника и 3 четырехугольника?

Как провести 2 линии чтобы получилось 3 треугольника и 3 четырехугольника.

Видео:Теорема о средней линии треугольника. Доказательство. 8 класс.Скачать

Провести в фигуре 2 линии чтобы получилось 2 треугольника и 6 четырехугольников?

Провести в фигуре 2 линии чтобы получилось 2 треугольника и 6 четырехугольников.

Видео:Средняя линия треугольника – 8 класс геометрияСкачать

Еще , в четырехугольнике провести два отрезка так, чтобы получились три треугольника и три четырехугольника?

Еще , в четырехугольнике провести два отрезка так, чтобы получились три треугольника и три четырехугольника.

Видео:МАТЕМАТИКА | Средняя линия треугольникаСкачать

Как провести 2 отрезка в треугольнике, что — бы получить два треугольника, один четырехугольник?

Как провести 2 отрезка в треугольнике, что — бы получить два треугольника, один четырехугольник.

Вы открыли страницу вопроса Как провести две линии в треугольнике что бы получилось два треугольника и один четырехугольник?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 1 — 4 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

1)Периметр — это сумма длин сторон Р = a + b + c = 30 см. 2) основание — с = 12 — дано 3) Треугольник равнобедренный — a = b 4) a + b = P — c = 30 — 12 = 18 см Находим стороны треугольника 5) a = b = 18 : 2 = 9 см — ОТВЕТ.

Решение вашего ЗаданиЯ.

АС = 0, 8Х10 = 8 Скорее всего так.

А) (23)² = 529 б) (36)² = 1296.

Нок 21 = 3 * 7 нок 25 = 5 * 5 нок = 3 * 7 * 5 * 5 = 525 дней они встретятся 525 : 21 = 25 рейсов для 1 525 : 25 = 21 рейс для 2.

1469 + 40177 = 111474 длина отрезка 147.

49 делится на 7 98 делится на 7 Следовательно, сумма 48 + 98 делится на 7.

Подсчитаем, сколько раз входит каждое число от 2 до 100 в произведение. 2 входит во все факториалы, начиная со второго, т. Е. 99 раз3 входит во все факториалы, начиная с третьего, т. Е. 98 разn входит во все факториалы, начиная с n, т. Е. 101 – n..

Наименьшее общее кратное знаменателей = 28 1 / 4 = (1 * 7) / (4 * 7) = 7 / 28 5 / 7 = (5 * 4) / (7 * 4) = 20 / 28 9 / 28 = — без изменений.