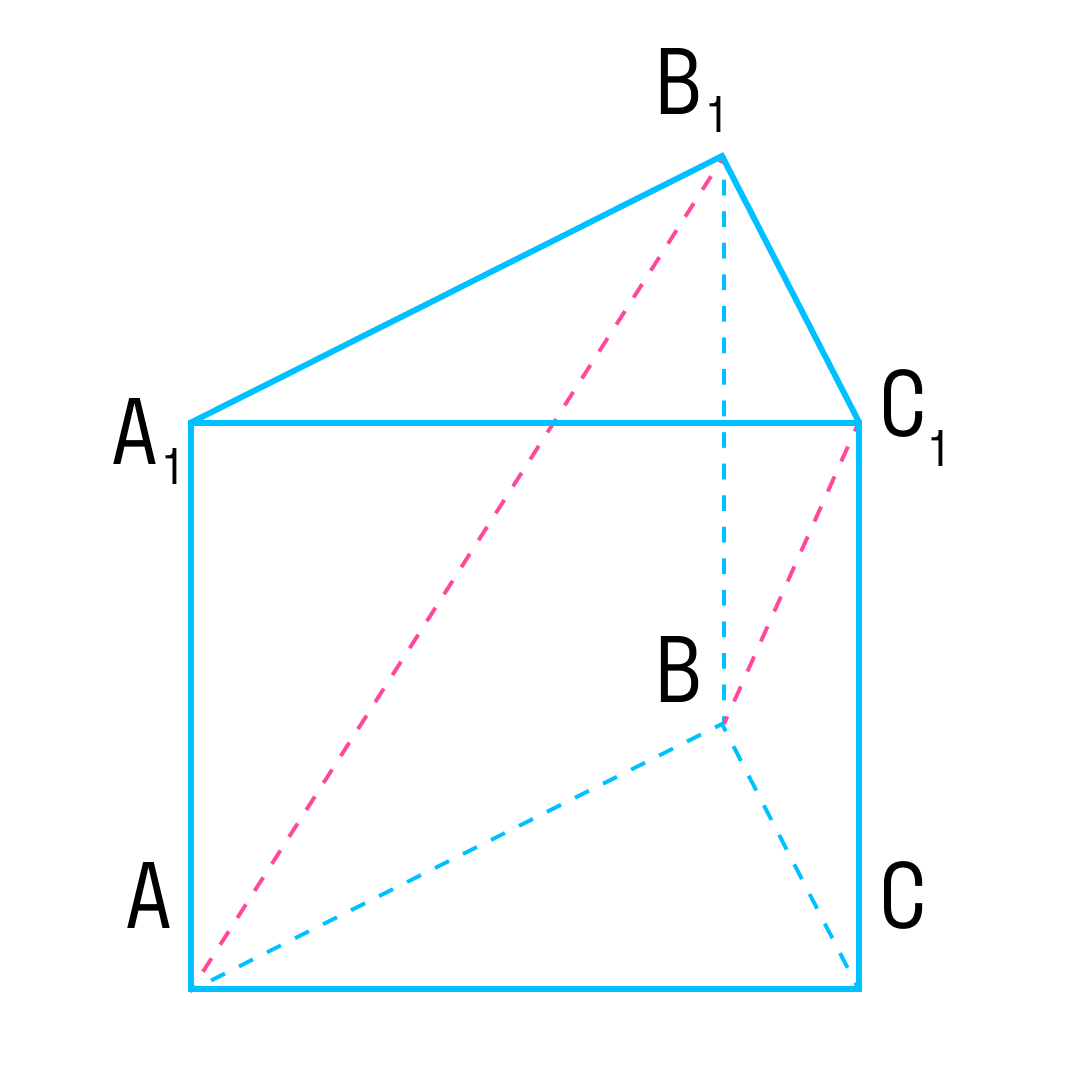
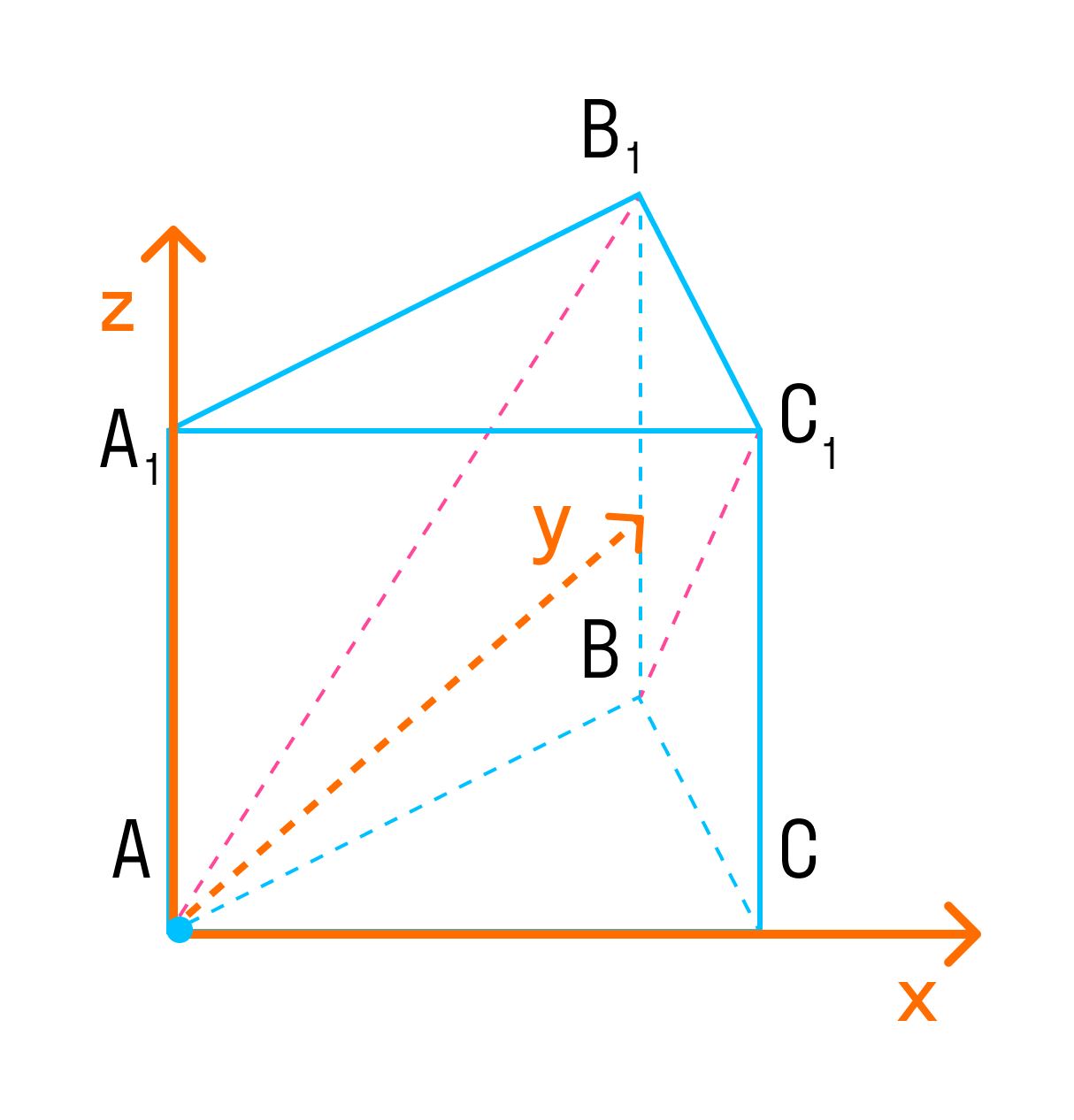
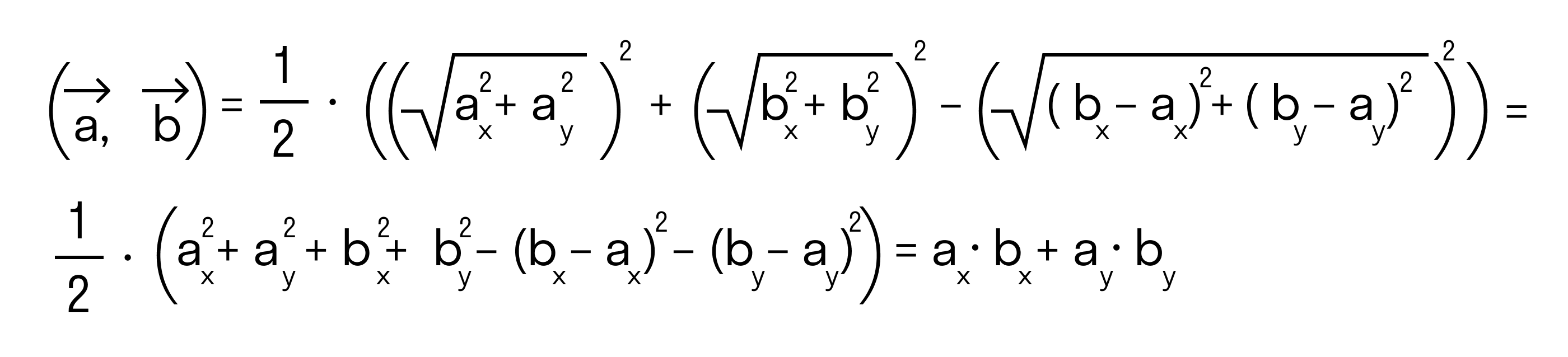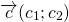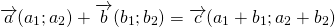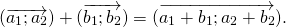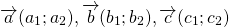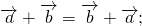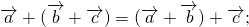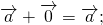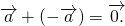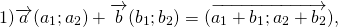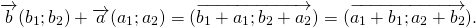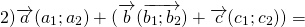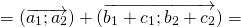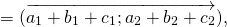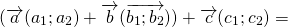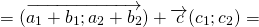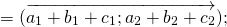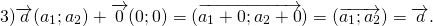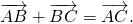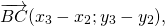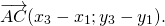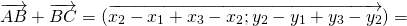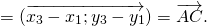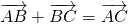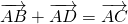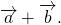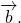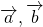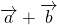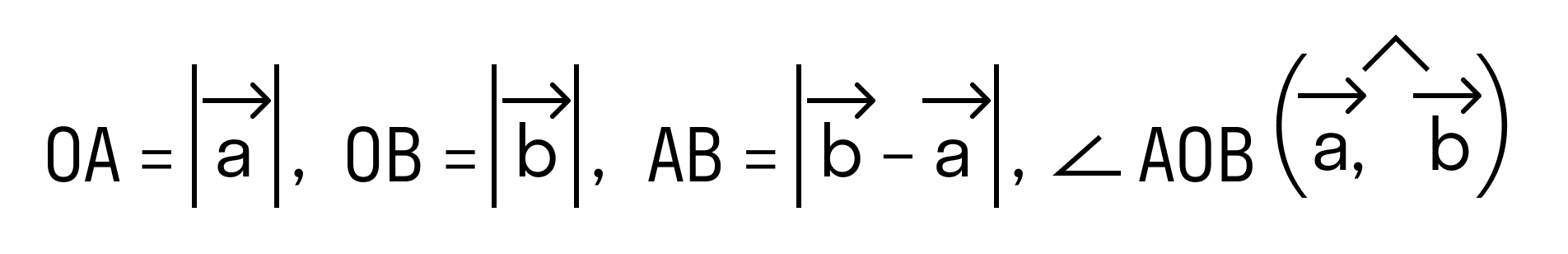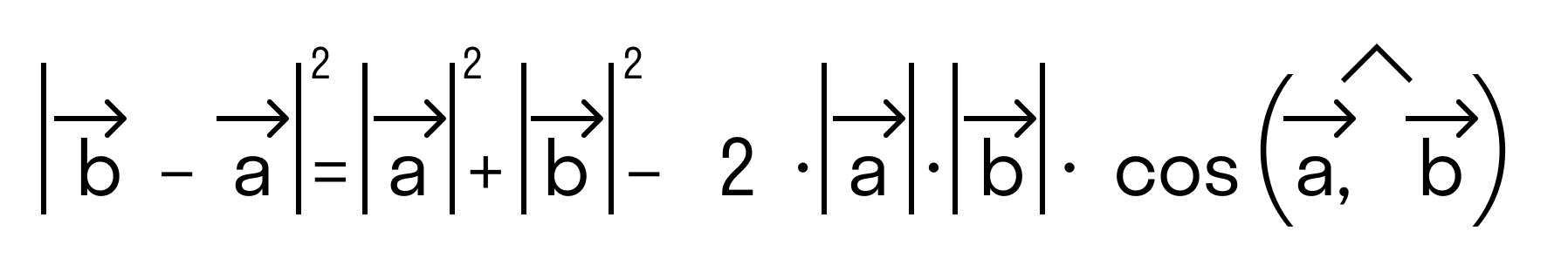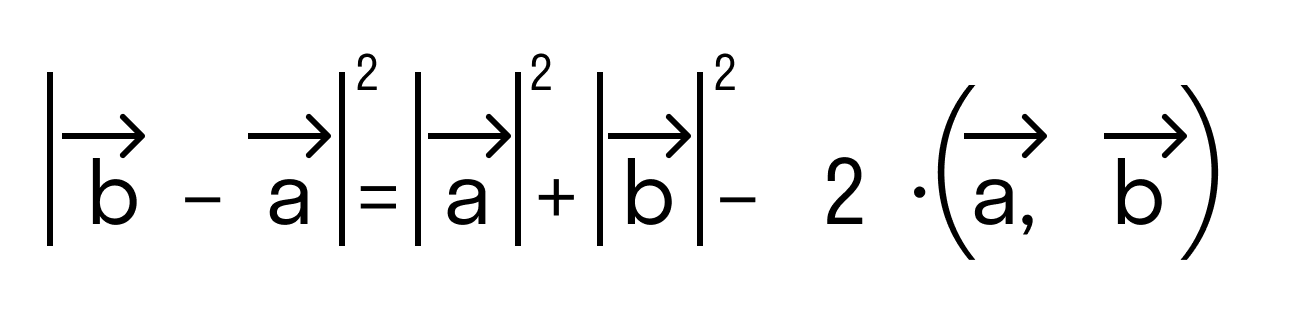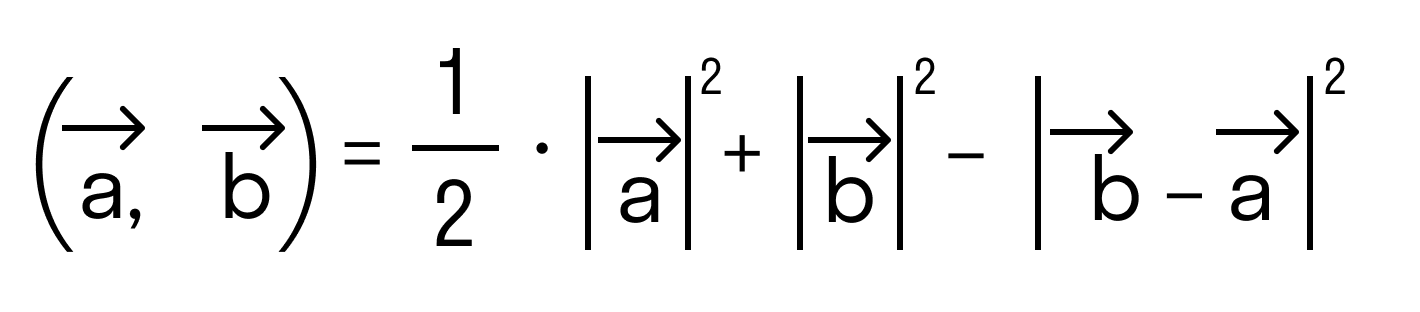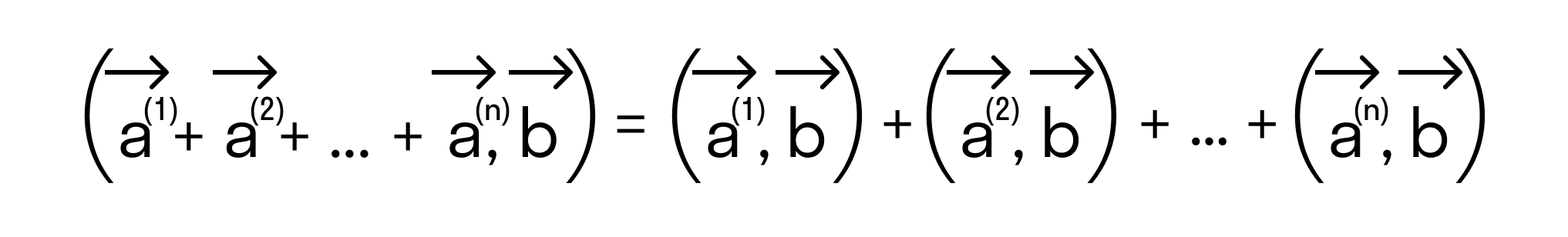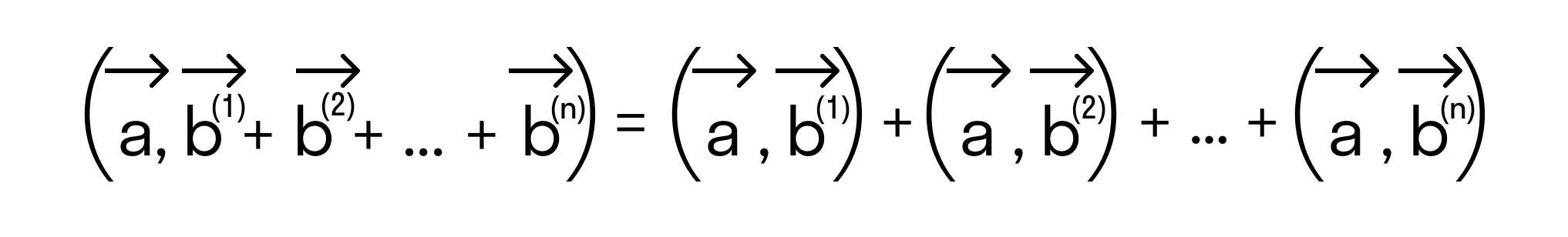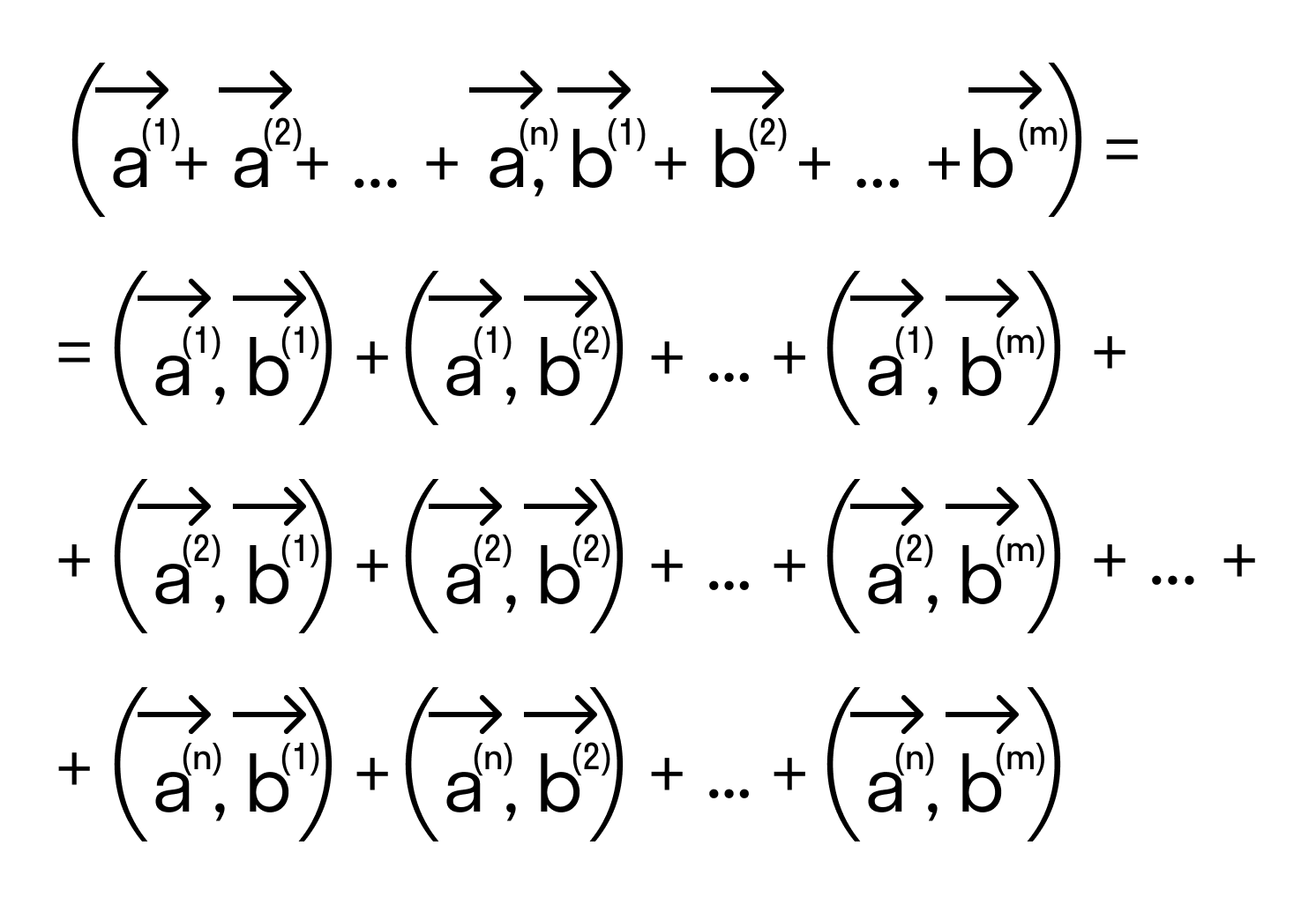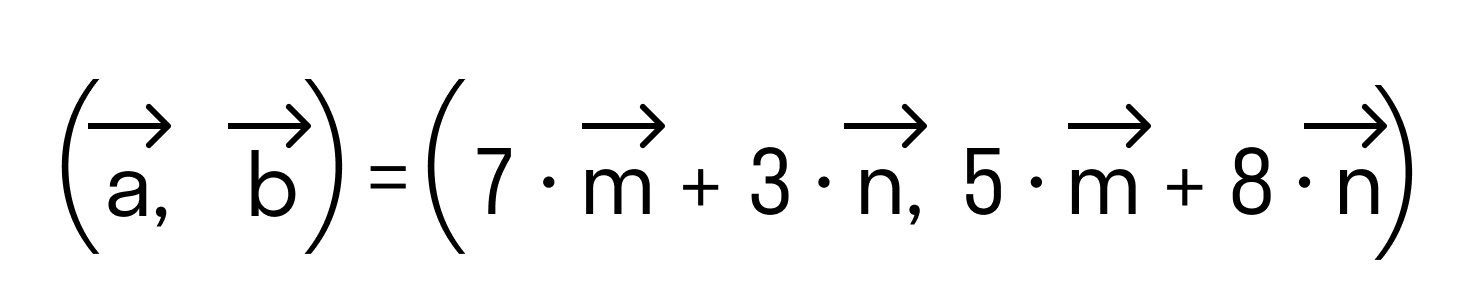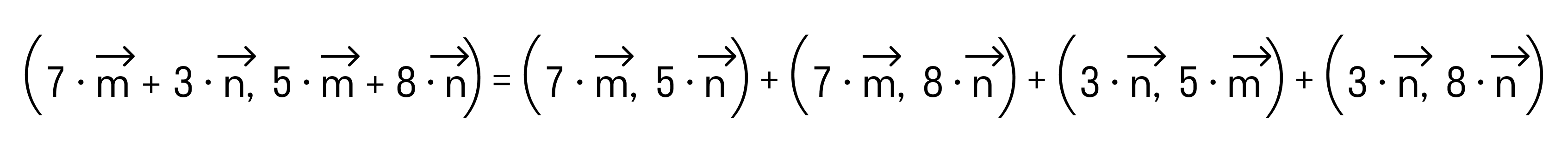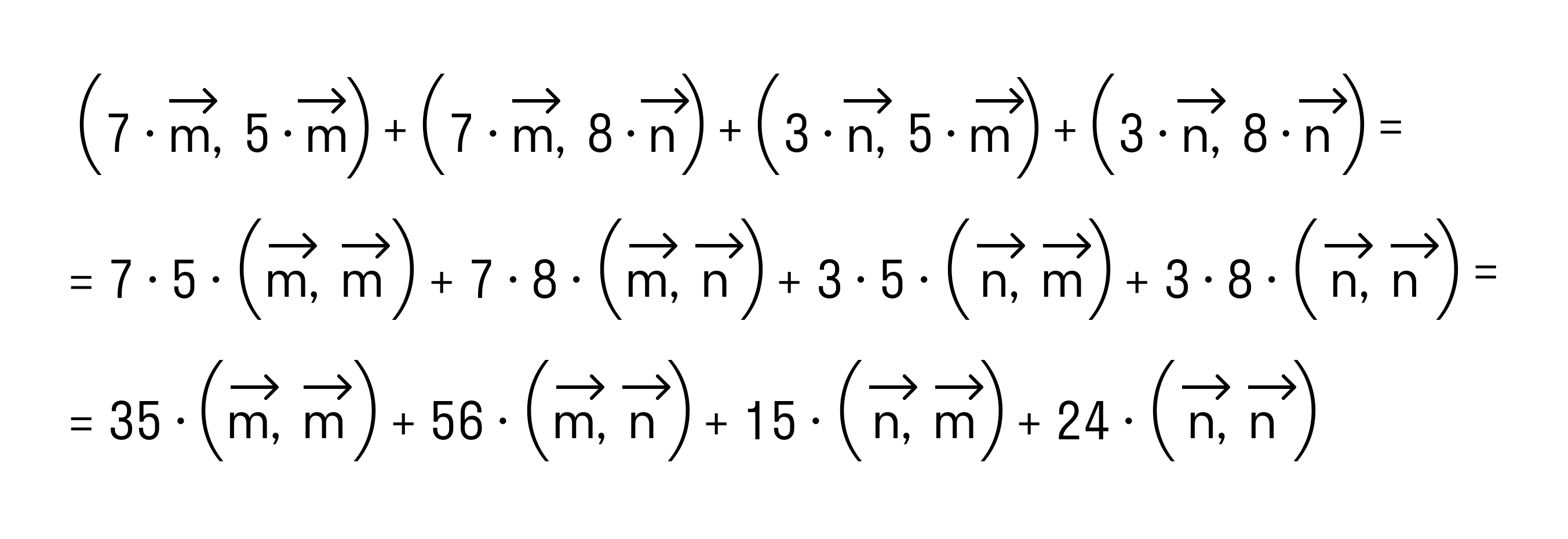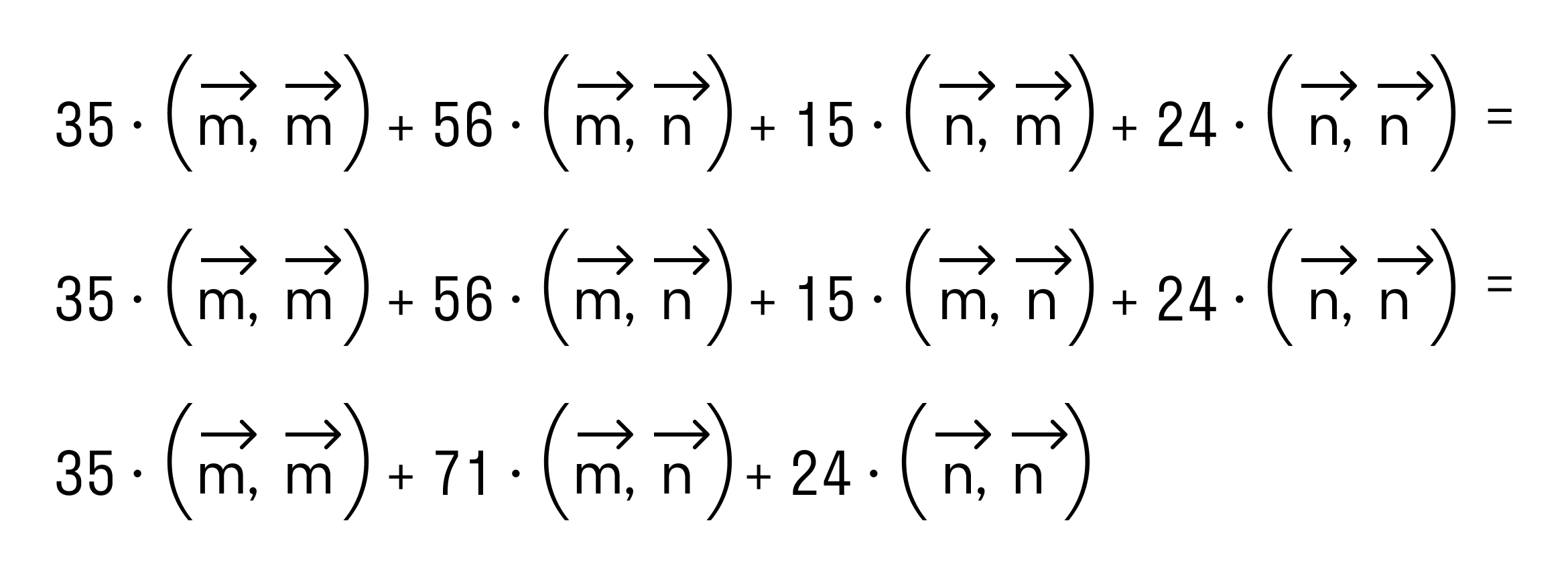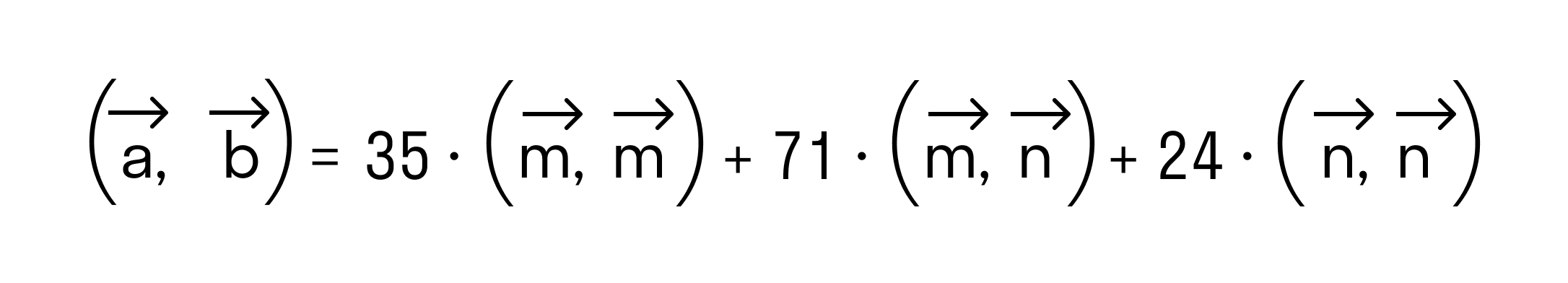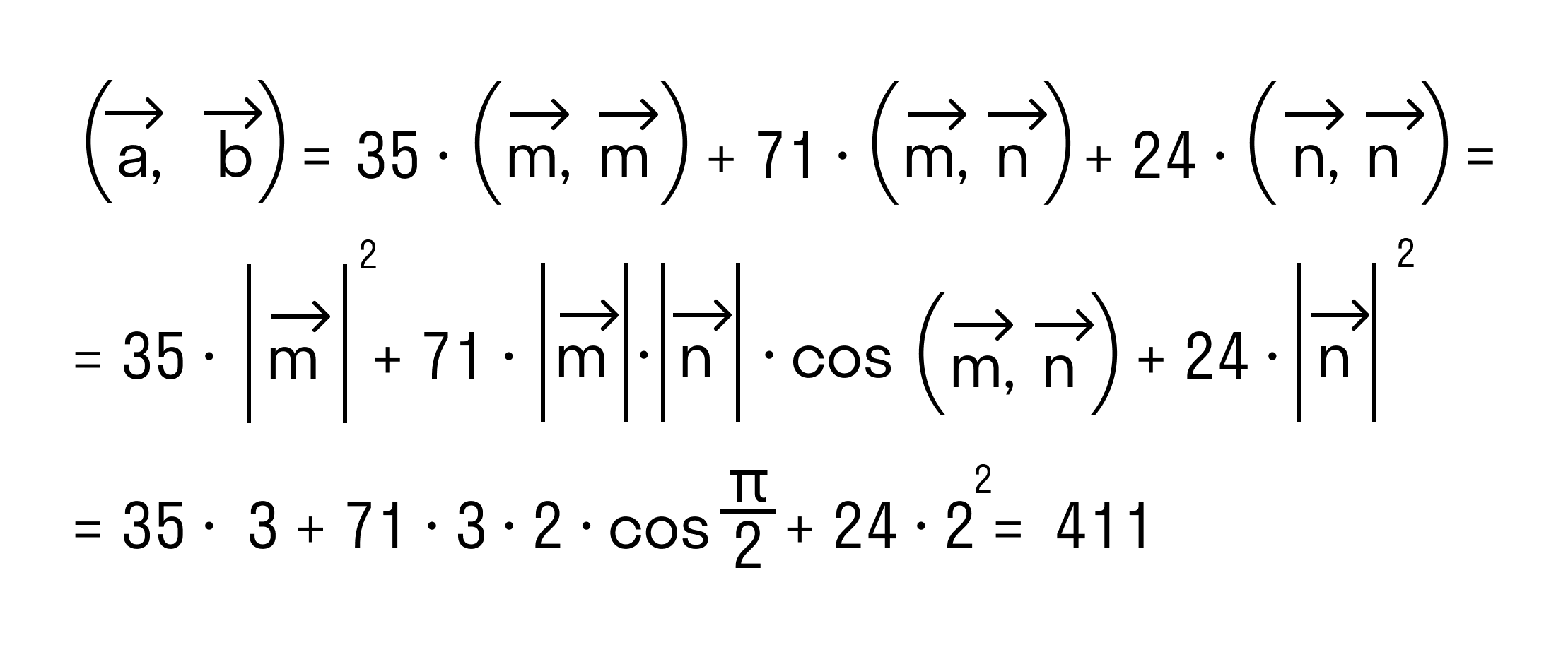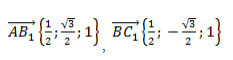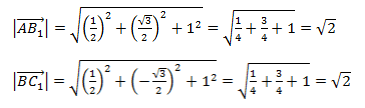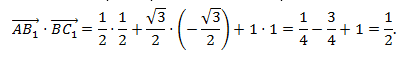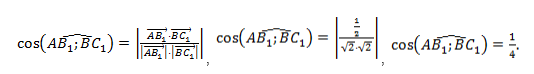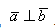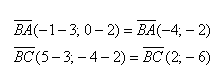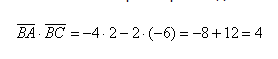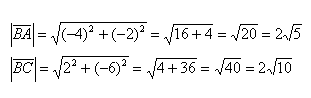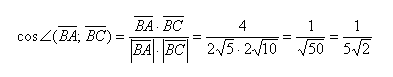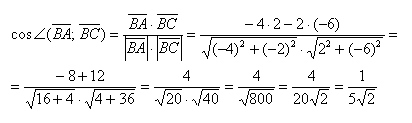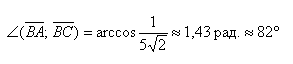Сумма векторов
Свойства сложения векторов:
Для любых векторов
3) свойство прибавления нулевого вектора:
4) сумма противоположных векторов равна нулевому вектору:
Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:
Так как соответствующие координаты равны, то эти векторы равны.
(О сложении векторов)
Каковы бы ни были точки A, B, C, имеет место векторное равенство:
Что и требовалось доказать.
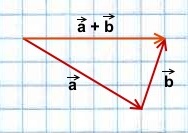
Правило треугольника построения суммы двух векторов
Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.
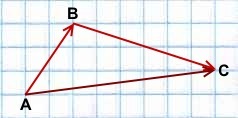
(то есть это правило следует из теоремы о сложении векторов).
Правило параллелограмма построения суммы двух векторов
Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.
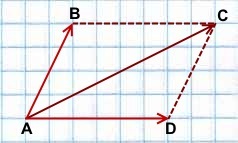
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.
При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.
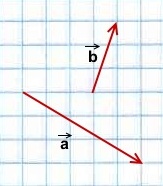
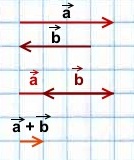
1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора
Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).
2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы
от общего начала.
Достроим на этих векторах параллелограмм.
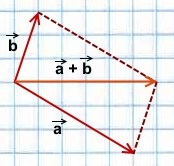
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.
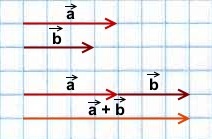
1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.
2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.
Фактически в обоих случаях мы используем правило треугольника сложения векторов:
от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.
Из неравенства треугольника следует ещё два свойства сложения векторов:
- Треугольник. Формулы определения и свойства треугольников.
- Определение треугольника
- Классификация треугольников
- 1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
- 2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
- 3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
- 4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
- 5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
- 6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
- Свойства треугольника
- 1.Свойства углов и сторон треугольника.
- 2.Теорема синусов.
- 3. Теорема косинусов.
- 4. Теорема о проекциях
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Скалярное произведение векторов
- Основные определения
- Угол между векторами
- Скалярное произведение векторов
- Скалярное произведение в координатах
- Формулы скалярного произведения векторов заданных координатами
- Свойства скалярного произведения
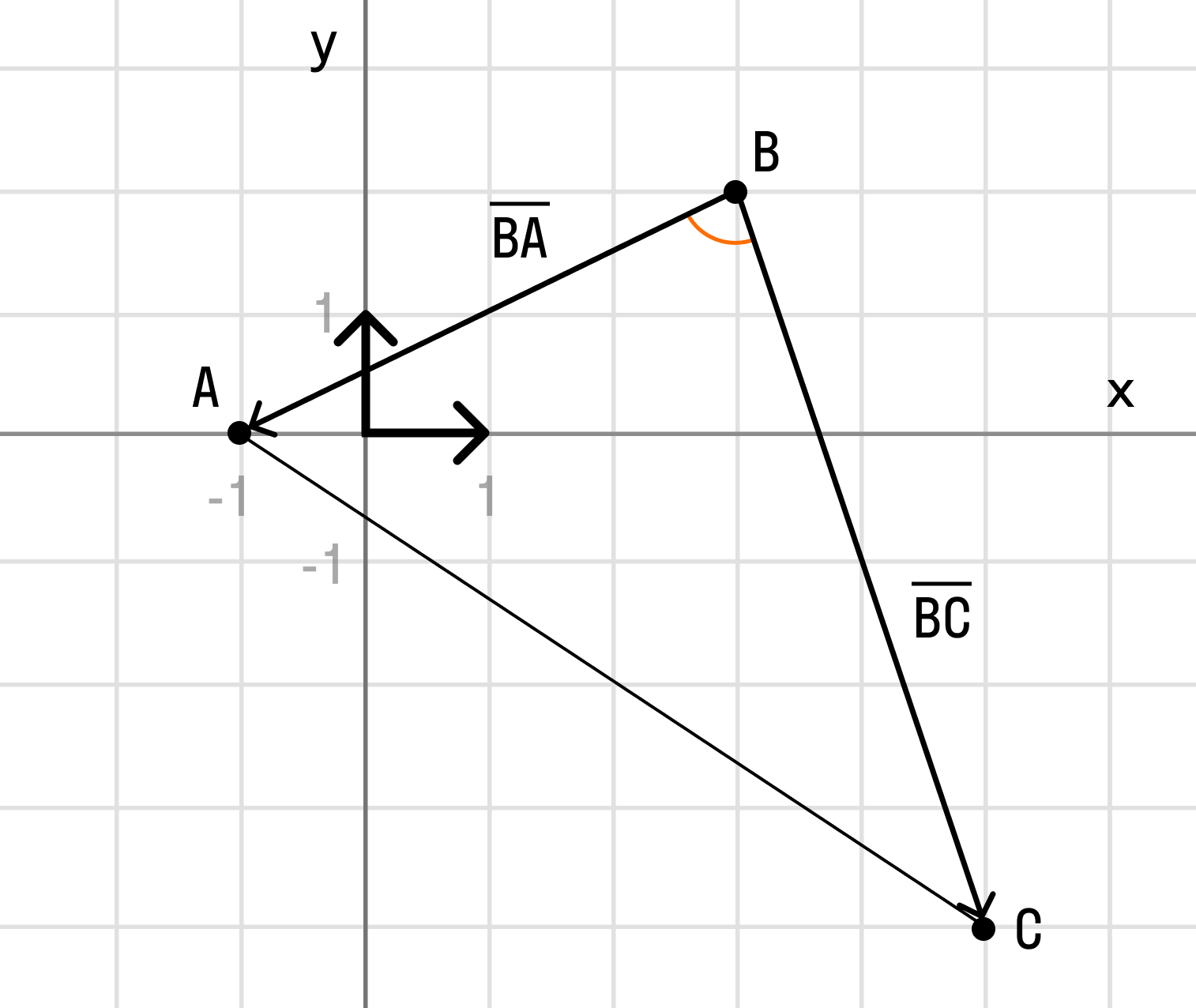
- Примеры вычислений скалярного произведения
- 💥 Видео
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
Видео:егэ векторы решу егэ все задания №2 профильСкачать

Определение треугольника
Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Треугольник ABC (△ABC)
- Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.
Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Видео:Уравнения стороны треугольника и медианыСкачать

Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

Свойства треугольника
1.Свойства углов и сторон треугольника.
- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны:
Видео:Скалярное произведение векторов. 9 класс.Скачать

Скалярное произведение векторов
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Основные определения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
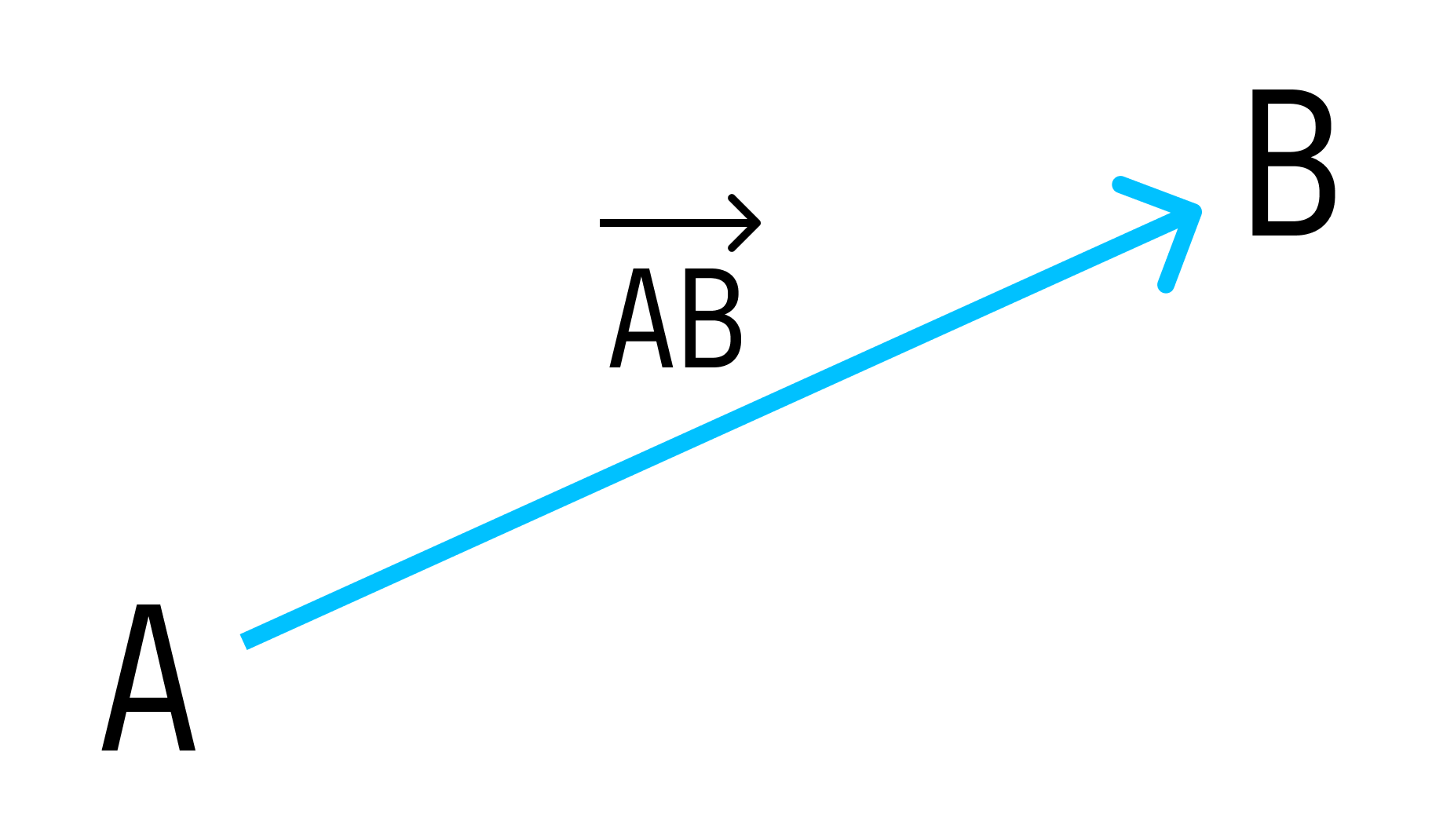
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.
Видео:Угол между векторами. 9 класс.Скачать

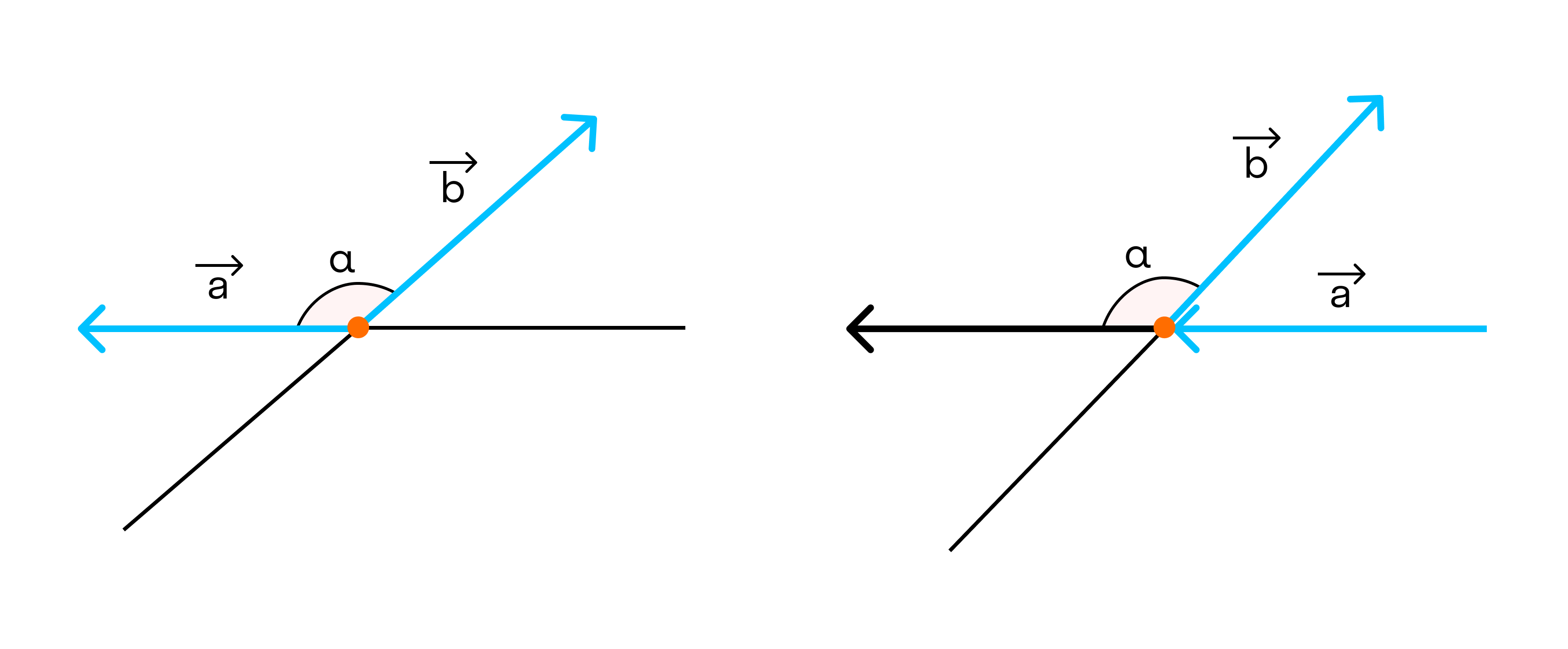
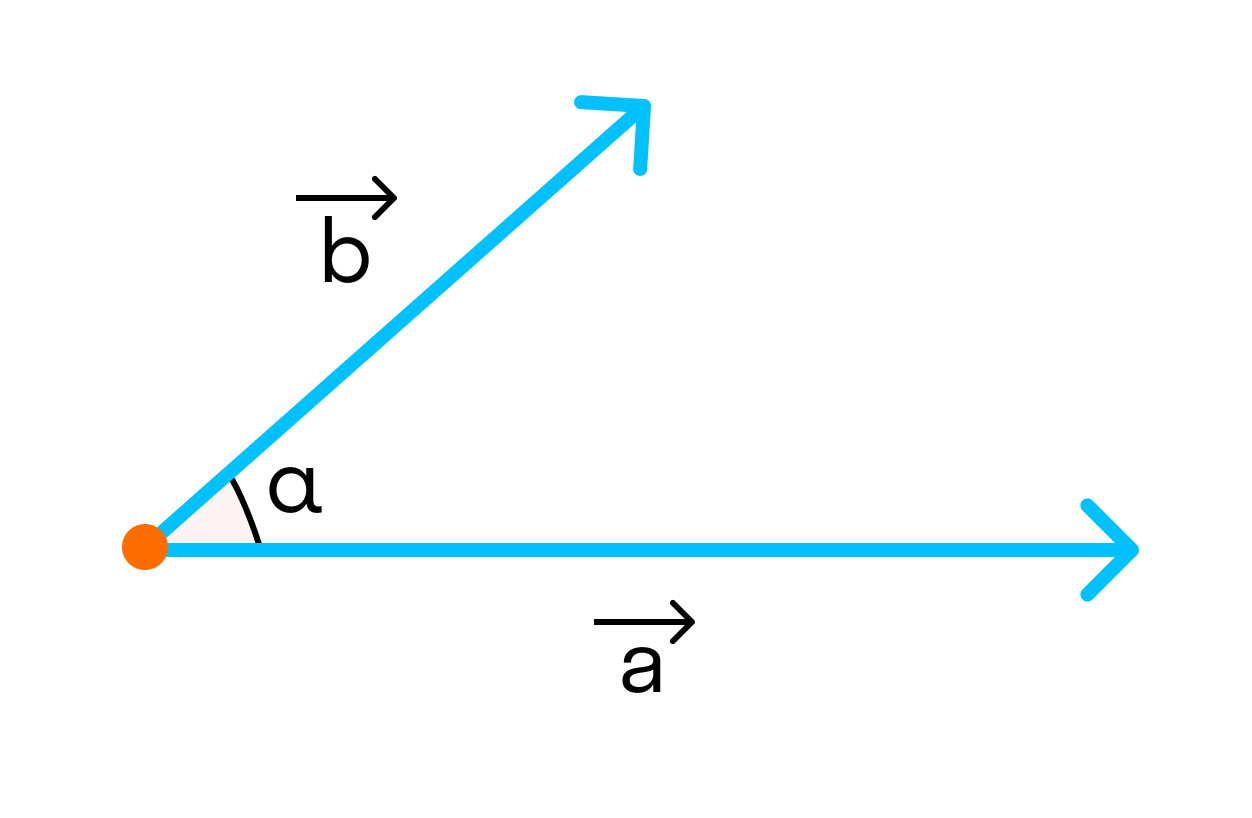
Угол между векторами
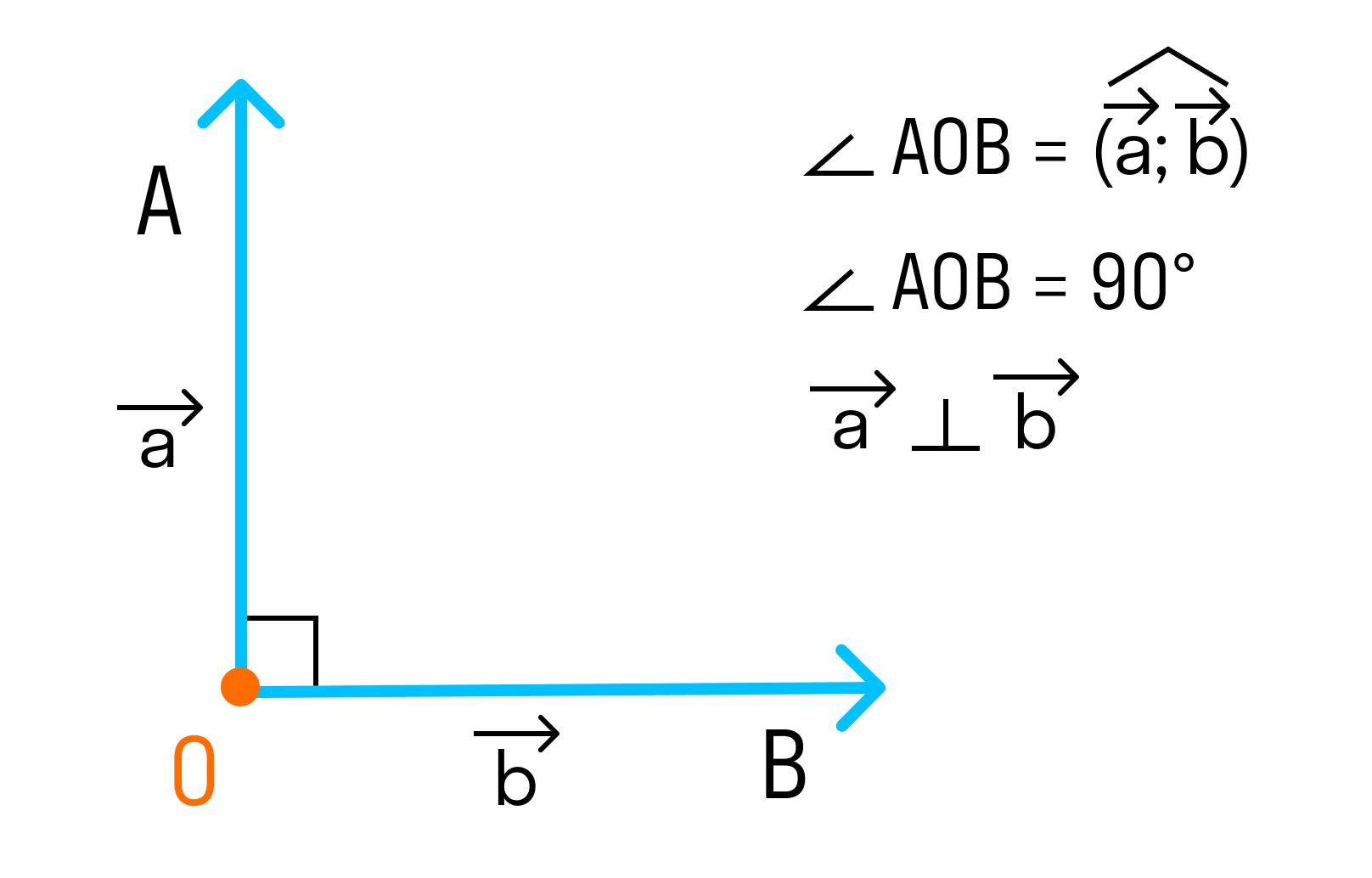
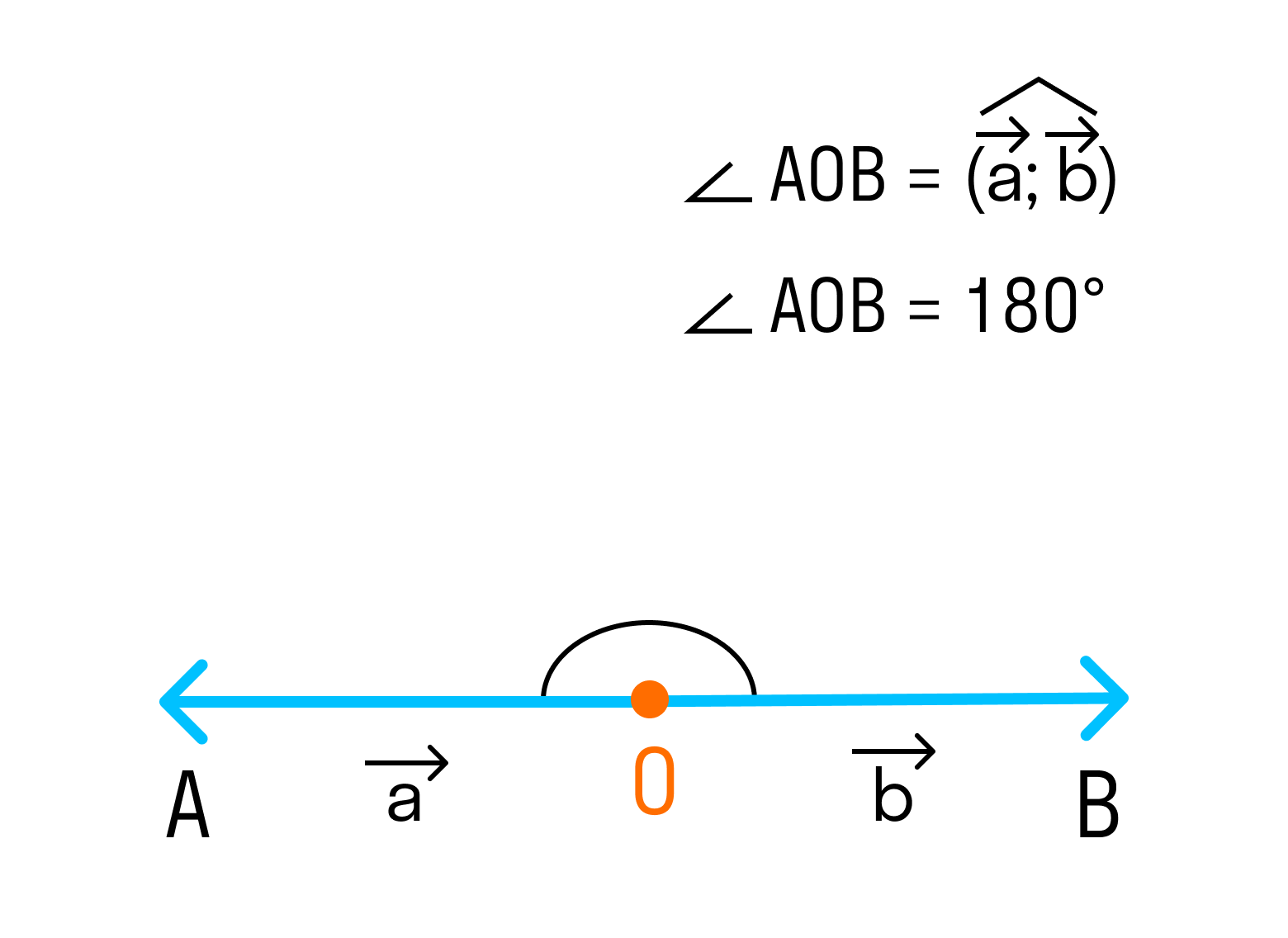
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
Также векторы могут образовывать тупой угол. Это выглядит так:
Видео:Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
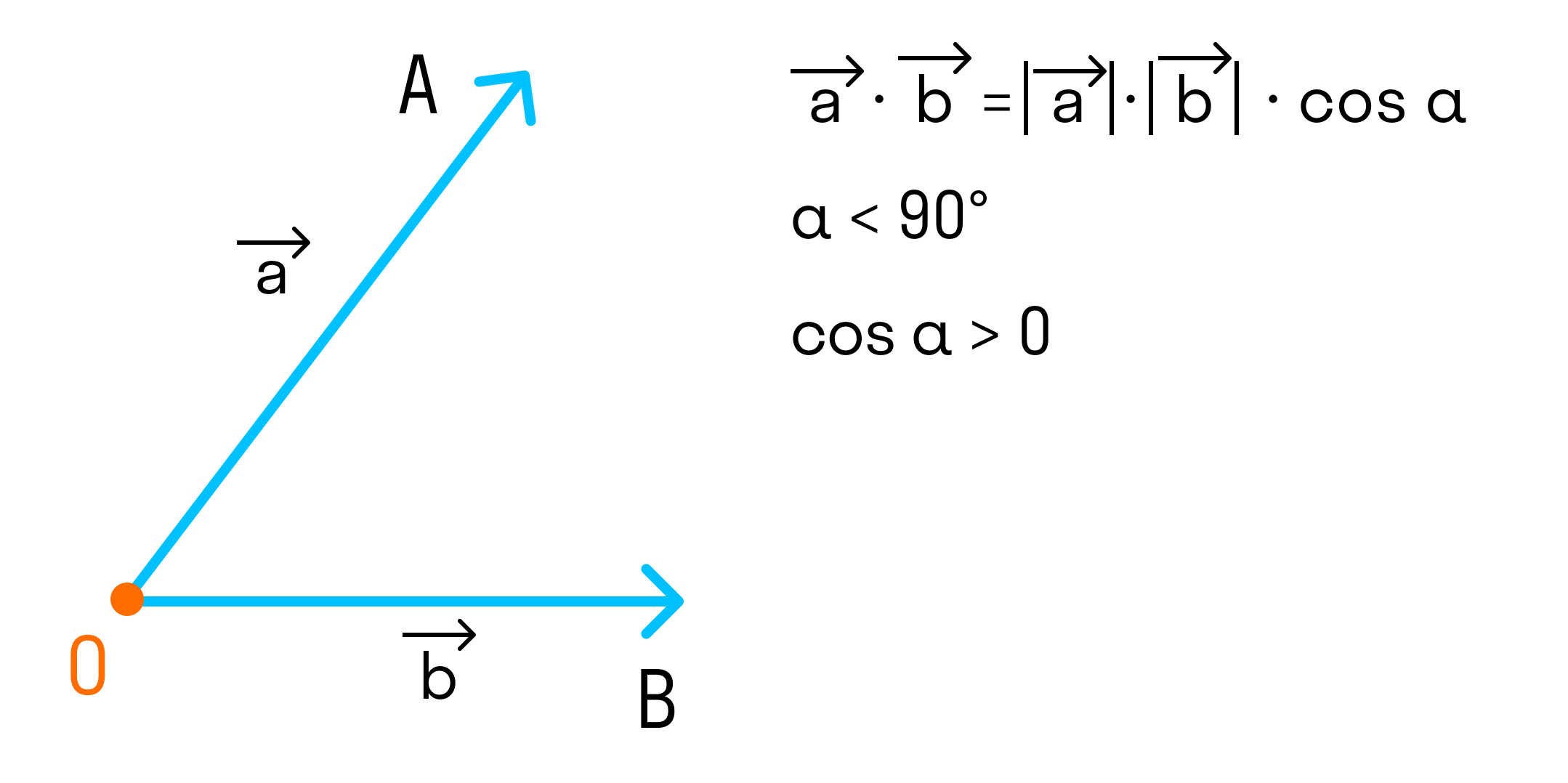
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
→a * →b = →|a| * →|b| * cosα
Что важно запомнить про геометрическую интерпретацию скалярного произведения:
- Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
- Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα
Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Скалярное произведение в координатах
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.
То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by
А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz
Докажем это определение:
Сначала докажем равенства
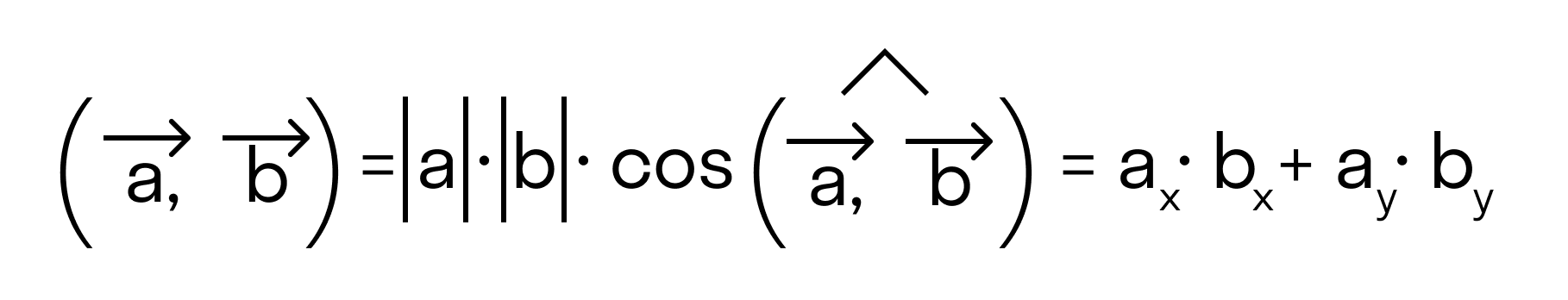
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.
Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)
Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)
Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:
то последнее равенство можно переписать так:
а по первому определению скалярного произведения имеем