В ΔАВС: ВО — медиана, а значит, и высота (ΔАВС — равнобедренный). Таким образом, ВО⊥АС.
В ΔADC: DO — медиана, а значит, и высота (ΔADC — равнобедренный). Таким образом, DO⊥АС.
Таким образом, к отрезку АС через точку О проведены два перпендикуляра. По теореме 2.3 через точку, лежащую на прямой, можно провести перпендикуляр, и притом единственный. Таким образом, медианы лежат на одной прямой.

задача №26
к главе «§ 3. Признаки равенства треугольников».
- Даны два равнобедренных треугольника с общим основанием?
- Верно ли что центр окружности, описанной около равнобедренного треугольника, лежит на прямой, содержащей его медиану, проведенную к основанию?
- Высота равнобедренного треугольника проведенная к основанию является медианой и биссектрисой?
- Докажите, что медиана прямоугольного треугольника , проведенная к его гипотенузе, делит данный треугольник на два равнобедренных треугольника?
- 47 БАЛЛОВ?
- Докажите что равнобедренные треугольники равны если равны их основания и высоты проведенные к основаниям?
- Найдите медианы?
- В равнобедренном треугольнике дано основание а и угол альфа при основании?
- Основание и боковая сторона одного равнобедренного треугольника равны 12см и 10см, а основание другого равнобедренного треугольникк и проведенная к нему медиана равны 18 см и 12 см?
- В равнобедренном треугольнике ABC с основанием AC проведите прямую через середины боковых сторон (у меня уже проведена) Докажите, что основание и проведенная прямая параллельны?
- Даны два равнобедренный треугольника ABC и ABD с общим основанием AB?
- Два треугольника с общим основанием
- 🔥 Видео
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Даны два равнобедренных треугольника с общим основанием?
Геометрия | 5 — 9 классы
Даны два равнобедренных треугольника с общим основанием.
Докажите, что их, медианы, проведенные к основанию, лежат на одной прямой.
Медианы лежат на одной прямой поэтому что и бессиктриса и высота тоже будут проведены к оснаванию.
Видео:№142. Равнобедренные треугольники ADC и BCD имеют общее основание DC. Прямая АВ пересекает отрезокСкачать

Верно ли что центр окружности, описанной около равнобедренного треугольника, лежит на прямой, содержащей его медиану, проведенную к основанию?
Верно ли что центр окружности, описанной около равнобедренного треугольника, лежит на прямой, содержащей его медиану, проведенную к основанию?
(Ответ поясните) Пояснение.
Медиана, проведенная к основанию, является и .
Этого треугольника, а следовательно, лежит на .
Видео:Площади треугольников с равным углом.Скачать

Высота равнобедренного треугольника проведенная к основанию является медианой и биссектрисой?
Высота равнобедренного треугольника проведенная к основанию является медианой и биссектрисой.
Медиана равнобедренного треугольника, проведенная к основанию является высотой и биссектрисой .
Докажите эти теоремы!
Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Докажите, что медиана прямоугольного треугольника , проведенная к его гипотенузе, делит данный треугольник на два равнобедренных треугольника?
Докажите, что медиана прямоугольного треугольника , проведенная к его гипотенузе, делит данный треугольник на два равнобедренных треугольника.
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

47 БАЛЛОВ?
Докажите, что если основание и медиана, проведенная к боковой стороне одного равнобедренного треугольника, равны основанию и медиане, проведенной к боковой стороне другого равнобедренного треугольника, то эти треугольники равны.
Заранее огромное спасибо.
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Докажите что равнобедренные треугольники равны если равны их основания и высоты проведенные к основаниям?
Докажите что равнобедренные треугольники равны если равны их основания и высоты проведенные к основаниям.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Найдите медианы?
Высота проведенная к основанию равнобедренного треугольника равна 6, а основание треугольника равна 20см.
Найдите медианы треугольника.
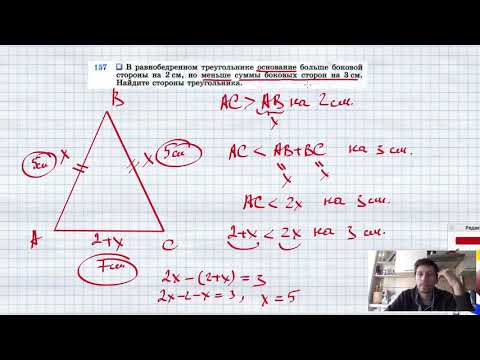
Видео:№157. В равнобедренном треугольнике основание больше боковой стороны на 2 см, но меньше суммы боковыСкачать
В равнобедренном треугольнике дано основание а и угол альфа при основании?
В равнобедренном треугольнике дано основание а и угол альфа при основании.
Найти длину медианы проведенной к боковой стороне.
Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Основание и боковая сторона одного равнобедренного треугольника равны 12см и 10см, а основание другого равнобедренного треугольникк и проведенная к нему медиана равны 18 см и 12 см?
Основание и боковая сторона одного равнобедренного треугольника равны 12см и 10см, а основание другого равнобедренного треугольникк и проведенная к нему медиана равны 18 см и 12 см.
Подобны ли данные треугольники?
Видео:Задачи на Треугольники Общего ВидаСкачать

В равнобедренном треугольнике ABC с основанием AC проведите прямую через середины боковых сторон (у меня уже проведена) Докажите, что основание и проведенная прямая параллельны?
В равнобедренном треугольнике ABC с основанием AC проведите прямую через середины боковых сторон (у меня уже проведена) Докажите, что основание и проведенная прямая параллельны.
Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Даны два равнобедренный треугольника ABC и ABD с общим основанием AB?
Даны два равнобедренный треугольника ABC и ABD с общим основанием AB.
Докажите, что AB и CD перпендикулярны, если точки C и D лежат по разные стороны от прямой AB.
Вы перешли к вопросу Даны два равнобедренных треугольника с общим основанием?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
Если две прямые на плоскости перпендикулярные одной и той же прямой, то они параллельны . Если при пересечении двух прямых третьей секущей : накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180°, то пря..
L = l = (3, 14 * 27 / 180) * 40 = 18, 84.
Так как угол равен АОВ 122 градуса то мы его делим на 2 и получаем ответь.
От угла АОВ = 122° отними сумму углов АОЕ и СОВ получается 122 — 19 — 23 = 86°.
Угол А = 30 угол В = 120 угол С = 30 угол АВD и BDC = 90 угол ABD и BDC = 60.
Ответ : 18 смОбъяснение : Диагонали прямоугольника равны и точкой пересечения делятся пополам, значитАО = ВО = АС / 2 = 12 / 2 = 6 см∠ВАС = ∠BAD — ∠CAD = 90° — 30° = 60°ΔАВО равнобедренный с основанием АВ, значит углы при основании равны : ∠ВАО = ∠АВ..
Сумма острых углов в прямоугольном треугольнике равна 90 градусов. X — больший угол. Х + 20 = 90 х = 90 — 20 = 70 градусов(больший угол).
Видео:#635 НАУКА Структура вакуума. Устройство Мироздания: версия Межзвездного Союза. Юмор в разных мирах.Скачать

Два треугольника с общим основанием
В элементарной математике, самыми трудными считаются геометрические задачи. Как научиться решать геометрические задачи, особенно сложные, конкурсные? При решении геометрических задач, как правило, алгоритмов нет, и выбирать наиболее подходящую к данному случаю теорему не просто. Поэтому, желательно в каждой теме выработать какие-то общие положения, которые полезно знать всякому решающему геометрические задачи.
Предлагаем один из алгоритмов решения многих геометрических задач – метод площадей, т.е. решение задач с использованием свойств площадей.
Основные свойства площадей.
Свойство №1
Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не измениться.

Свойство №2

Рассмотрим отношение площадей этих треугольников $$frac<S_><S_>= frac<frac cdot a cdot h_><frac cdot b cdot h_>$$.
Упростив, получим $$frac<S_><S_>= frac$$.
Свойство №3 Если два треугольника имеют общий |  |  | Доказательство: Рассмотрим ▲ABC и ▲MBN . Пусть AB = k MB, BC = k NB и $$angle ABC = angle MBN$$. Используя формулу площади треугольника вида $$S = frac cdot a cdot b cdot singamma$$ , рассмотрим отношение подобных площадей ▲ABC и ▲MBN . Тогда $$frac<S_><S_> = frac<frac cdot AB cdot BC cdot sin B><frac cdot MB cdot NB cdot sin B>= frac = k^$$ . |
Медиана треугольника делит его на две равновеликие части.

Свойство №6
Медианы треугольника делят его на три равновеликие части.

Средние линии треугольника площади S отсекают от него треугольники площади .


















