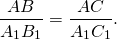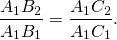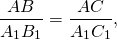Доказательство второго подобия треугольников (3 видео)

Основные сведения о втором признаке подобия треугольников

Содержание

Основные понятия
Теорема о втором признаке подобия треугольников
Доказательство:
Примеры решения задач
Второй признак подобия треугольников
Подобные треугольники
Определение
Признаки подобия треугольников
Свойства подобных треугольников
Примеры наиболее часто встречающихся подобных треугольников
📸 Видео

Видео:Второй признак подобия треугольников. Доказательство. 8 класс.Скачать

Основные понятия

Треугольник — геометрическая фигура, имеющая три соединенных стороны и три угла. Сумма всех углов любого треугольника равна 180°.

Видео:8 класс, 23 урок, Второй признак подобия треугольниковСкачать

Теорема о втором признаке подобия треугольников

Теорема гласит: если две стороны одного треугольника пропорциональны двум другим сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Доказательство:

Даны треугольники ABC и DEF. Докажем, что они являются подобными.

Достроим к ▵ A B C точку G. Получаем ▵ A G B , у которого ∠ 1 = ∠ D ; ∠ 2 = ∠ F .

Согласно первому признаку подобия треугольников, ▵ D E F

▵ A G B (по двум углам).

Следует, что AB так относится к DF, как AG к DE. A B D F = A G D E .
Нам известно, что A B D F = A C D E . Следовательно, A G D E = A C D E . Таким образом, A G = A C .
Получается, что ▵ A G B = ▵ A C B (по двум сторонам и углу между ними, AB — общая, A G = A C , ∠ A = ∠ 1 , т.к. ∠ A = ∠ D и ∠ 1 = ∠ D ) .
Из всего этого следует, что ∠ B = ∠ 2 , а т.к. ∠ 2 = ∠ F , то ∠ B = ∠ F .
У треугольников ABC и DEF : ∠ A = ∠ D и ∠ B = ∠ F = > ▵ A B C

Что и требовалось доказать.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Примеры решения задач

Дано: ∠ C = ∠ F = 49 ° ; E F = 6 ; D F = 10 ; A B = 3

Оба треугольника прямые, ∠ C = ∠ F = 49 ° . Следовательно, эти треугольники подобны (по двум углам).
По теореме Пифагора найдем второй катет треугольника D E F . Он равен 8.
Составим пропорцию с использованием подобия треугольников. 6 3 = 8 A C = > A C = 4

Ответ: 4

Дано: ∠ D = 62 ° ; ∠ C = 56 °

▵ D E F — равнобедренный = > ∠ E = 62 ° = > ∠ F = 56 ° .
∠ F = 56 ° = > ▵ A B C

▵ D E F (по двум сторонам и углу между ними).

Составляем пропорцию подобия: 12 3 = C B 8 = > C B = 32

Видео:Второй и третий признаки подобия треугольников (доказательство) - 8 класс геометрияСкачать

Второй признак подобия треугольников

(Второй признак подобия треугольников — подобие треугольников по двум пропорциональным сторонам и углу между ними)

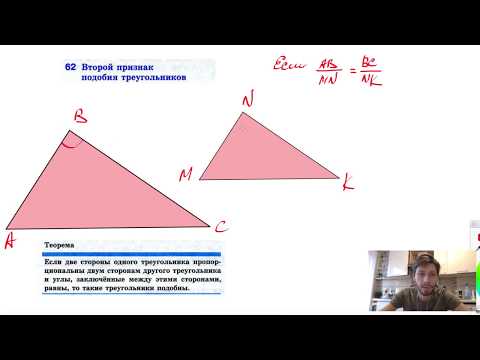
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

Дано: ΔABC, ΔA₁B₁C₁,

1) Отложим на луче A₁B₁ отрезок A₁B₂, A₁B₂=AB.

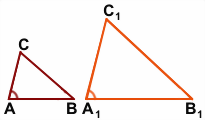
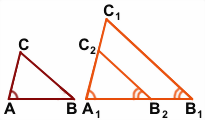
2) Через точку B₂ проведём прямую B₂С₂, параллельную прямой B₁C₁.

Из подобия треугольников следует пропорциональность соответствующих сторон:

Из равенства треугольников следует равенство соответствующих углов: ∠ABC=∠A₁B₂C₂.

Видео:Третий признак подобия треугольников. Доказательство. 8 класс.Скачать

Подобные треугольники

Видео:Геометрия 8 класс. Второй признак подобия треугольниковСкачать

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:Первый признак подобия треугольников. Доказательство. 8 класс.Скачать

Признаки подобия треугольников

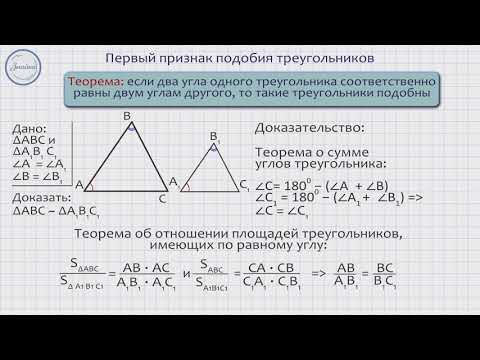
I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Свойства подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.