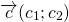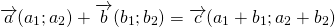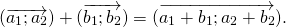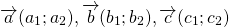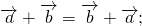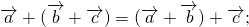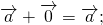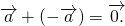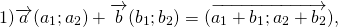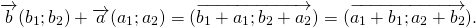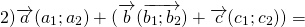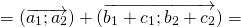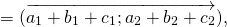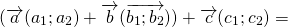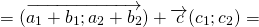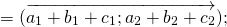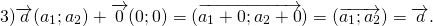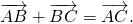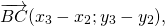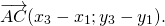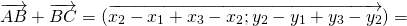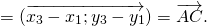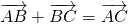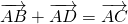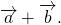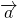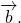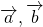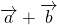Доказательство равнобедренного треугольника по векторам

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

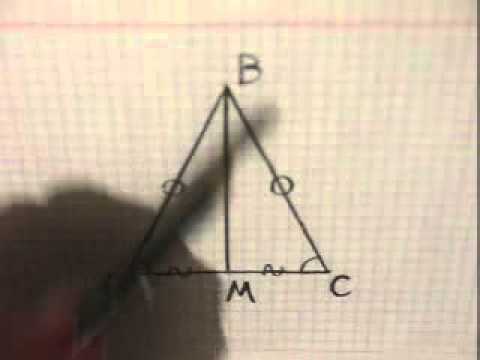
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Доказательство равнобедренного треугольника по векторам

Видео:Почему углы при основании равны в равнобедренном треугольникеСкачать

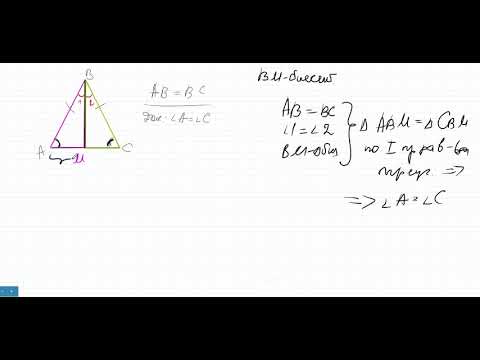
Даны координаты вершин треугольника ABC: А (-6; 1), В (2; 4), С (2; -2). Докажите, что треугольник ABC равнобедренный, и найдите высоту

Видео:Равнобедренный треугольник. 7 класс.Скачать

Ваш ответ

Видео:Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

решение вопроса

Видео:Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,921
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Задача, которую боятсяСкачать

Сложение векторов

Сумма векторов

Свойства сложения векторов:

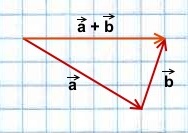
Для любых векторов

3) свойство прибавления нулевого вектора:

4) сумма противоположных векторов равна нулевому вектору:

Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:

Так как соответствующие координаты равны, то эти векторы равны.

(О сложении векторов)

Каковы бы ни были точки A, B, C, имеет место векторное равенство:

Что и требовалось доказать.

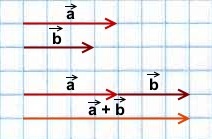
Правило треугольника построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.

Например,

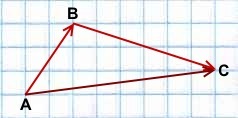
(то есть это правило следует из теоремы о сложении векторов).

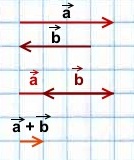
Правило параллелограмма построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.

Например,

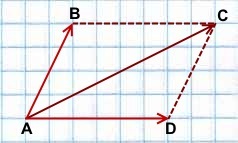
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.

При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.

Построить сумму векторов

1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора

Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).

2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы

от общего начала.

Достроим на этих векторах параллелограмм.

Сумма

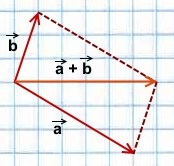
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.

1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.

2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.

Фактически в обоих случаях мы используем правило треугольника сложения векторов:

от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.

Из неравенства треугольника следует ещё два свойства сложения векторов:

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Вектор а (2 ; 1 — 8) Вектор б(1 ; — 5 ; 0) Вектор с(8 ; 1 ; — 4) Докажите, что треугольник АВС равнобедренный Найти длину ср линии треуголтника с соединяющей середины боковых сторон?

Геометрия | 10 — 11 классы

Вектор а (2 ; 1 — 8) Вектор б(1 ; — 5 ; 0) Вектор с(8 ; 1 ; — 4) Докажите, что треугольник АВС равнобедренный Найти длину ср линии треуголтника с соединяющей середины боковых сторон.

|AB| = √((1 — 2)² + ( — 5 — 1)² + (0 — ( — 8))²) = √(1 + 36 + 64) = √101

|BC| = √((8 — 1)² + (1 — ( — 5))² + ( — 4 — 0)²) = √(49 + 36 + 16) = √101

|AC| = √((8 — 2)² + (1 — 1)² + ( — 4 — ( — 8))²) = √(36 + 0 + 16) = √52

AB = BC, ⇒ΔABC — равнобедренный

MN||AC, MN = (1 / 2)AC

|MN| = √52 / 2, √52 / 2 = √(13 * 4) / 2 = 2√13 / 2 = √13

Видео:Свойства равнобедренного треугольника. Практическая часть. 7 класс.Скачать

В равнобедренном треугольнике с боковой стороной a, и высотой h, проведенной к основанию, найдите длину вектора, совпадающего с медианой, проведенной к боковой стороне?

В равнобедренном треугольнике с боковой стороной a, и высотой h, проведенной к основанию, найдите длину вектора, совпадающего с медианой, проведенной к боковой стороне.

Видео:Формулы равностороннего треугольника #shortsСкачать

Сторона равностороннего треугольника АВС равна а?

Сторона равностороннего треугольника АВС равна а.

Найти вектора |АВ + ВС|.

Видео:Как доказать теорему о медианах треугольника с использованием методов векторной алгебры?Скачать

В треугольнике ABC M — середина BC, Е — середина стороны АМ?

В треугольнике ABC M — середина BC, Е — середина стороны АМ.

Разложите вектор АЕ по векторам АВ = а ; АС = в.

Видео:Теорема о свойстве медианы равнобедренного треугольникаСкачать

Дан равносторонний треугольник АВС со стороной а?

Дан равносторонний треугольник АВС со стороной а.

Найдите : 1)векторы | АВ + ВС | 2) векторы | АВ + АС | 3)векторы | АВ + СВ | 4)векторы | ВА — ВС | 5)векторы|АВ — АС|.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

В треугольнике АВС проведена медиана AD?

В треугольнике АВС проведена медиана AD.

Докажите равенство вектор BD = вектор DC.

Видео:Признаки равнобедренного треугольника - геометрия 7 классСкачать

Дан треугольник АВС Вектор АВ = с вектор ВС = а вектор СА = в?

Дан треугольник АВС Вектор АВ = с вектор ВС = а вектор СА = в.

Чему равен вектор ВА.

Видео:Равнобедренный треугольник. Практическая часть. 7 класс.Скачать

В параллелограмме ABCD точки M и N — середины сторон BC и CD?

В параллелограмме ABCD точки M и N — середины сторон BC и CD.

AB = вектору a, AD = вектору b.

Выразите векторы AN и DM через векторы a и b.

Докажите, что векторы неколлинеарны.

Видео:ПРИЗНАКИ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА. §10 геометрия 7 классСкачать

В треугольнику АВС о — точка пересечения медиан?

В треугольнику АВС о — точка пересечения медиан.

Вырази вектор ОА через вектор а = вектору АВ, вектор в = вектору АС.

Видео:№163. Докажите, что середины сторон равнобедренного треугольника являются вершинами другого равнобедСкачать

Дан треугольник АВС?

Дан треугольник АВС.

Выразите через векторы (вектор) a = (вектор) BC и (вектор)b = (вектор) АС следующие векторы : а) вектор BA б)вектор СВ в)векторы СВ + ВА.

Докажите равенство отрезков, соединяющих середину основания равнобедренного треугольника с серединами боковых сторон?

Докажите равенство отрезков, соединяющих середину основания равнобедренного треугольника с серединами боковых сторон.

Вопрос Вектор а (2 ; 1 — 8) Вектор б(1 ; — 5 ; 0) Вектор с(8 ; 1 ; — 4) Докажите, что треугольник АВС равнобедренный Найти длину ср линии треуголтника с соединяющей середины боковых сторон?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 10 — 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

1. BD = AB–(AC + CD) = 15–(6 + 7) = 2 см 2. AK + BK = AB ; AK = 3BK 3BK + BK = AB = 36 4BK = AB = 36 BK = 36 : 4 = 9 AK = 3BK = 3 * 9 = 27 см.

С принадлежит АВ, D принадлежит СВ, BD — ? АВ = АС + СD + DВ ВD = АВ — АС — СD BD = 15 — 7 — 6 BD = 2.

АВ = √(1 — ( — 3))² + ( — 5 — 2)² = √4² + ( — 7)² = √65 длина отрезка. Х = — 3 + 1 / 2 = — 2 / 2 = — 1 у = 2 — 5 2 = — 3 / 2 = — 1, 5 ( — 1, — 1, 5) — координаты середины отрезка.

Где вопрос напиши я помогу тебе.

Доказываетсяпо первому признаку равенства треугольников. Из условия дано, что ОD = ОF и ОС = ОЕ. Прямые DF и СЕ образуют вертикальные углы COD и EOF равные между собой. Следовательно, раз в треугольниках COD и EOF две стороны и угол между ними рав..

∠АСВ = ∠САД = α как накрест лежащие, ∠ВАС = ∠ВСА = α как лежащие у основания равнобедренного треугольника, значит∠ВАД = 2α. ∠АВС = 180 — ∠ВАД = 180 — 2α. S(АВС) = a²·sin(180 — 2α) / 2 = (a²·sin2α) / 2. По теореме косинусов АС² = АВ² + ВС² — 2АВ·ВС..

9. AB = BD⇒∠BAD = ∠D = (180° — ∠B) / 2 = 90° — ∠B / 2 = 90° — 30° / 2 = 75°. ∠ACD = 180° — (∠D + ∠ DAC) = 180° — (75° + 75° / 2) = 180° — 112° 30′ = 67° 30′ . * * * ∠ BAC = ∠ DAC = ∠BAD / 2 * * * ответ : →В)67° 30′ . = = = = = = = 10. ∠C = 90° ∠A..

Мы знаем, что сумма острых углов прямоугольного треугольника равна 90 Получается из равенства, что 2А + 3В = 2(А + В) + В = 2 * 90 + В = 222 = > В = 42. Значит, А = 48 градусов = > Их разность равна 48 — 42 = 6.

У них углы прямые пэтому аб и цд / /.

Высота в принципе не нужна, 180° — (90° + 35°) = 55°.

Даны координаты вершин треугольника ABC: А (-6; 1), В (2; 4), С (2; -2). Докажите, что треугольник ABC равнобедренный, и найдите высоту

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,288
• гуманитарные 33,620
• юридические 17,900
• школьный раздел 607,127
• разное 16,830

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.