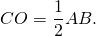Доказательство медиан прямоугольных треугольников (4 видео)

Свойства медианы в прямоугольном треугольнике с доказательствами

В этой статье мы рассмотрим свойства медианы в прямоугольном треугольнике, а также их доказательства.

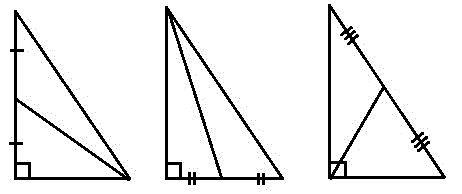
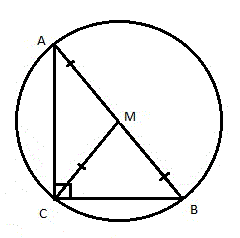
Медиана — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Для прямоугольного треугольника это будут медианы, проведённые с острого угла к серединам катетов или с прямого к центру гипотенузы (рис. 1).

Содержание

Свойства медианы в прямоугольном треугольнике
Доказательства свойств
Первое свойство
Доказательство:
Второе свойство
Доказательство:
Третье свойство
Доказательство:
Медиана, проведенная к гипотенузе
Определение и свойства медианы прямоугольного треугольника
Определение медианы прямоугольного треугольника
Свойство 1
Свойство 2
Свойство 3
Пример задачи
🔥 Видео

Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Свойства медианы в прямоугольном треугольнике

Медианы в прямоугольном треугольнике пересекаются в одной точке, а точка пересечения делит их в соотношении два к одному считая от вершины, из которой проведена медиана.
Медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы.
Медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Видео:Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать

Доказательства свойств

Первое свойство

Доказать, что медианы в прямоугольном треугольнике пересекаются в одной точке и делятся в пропорции 2:1, считая от вершины.

Доказательство:

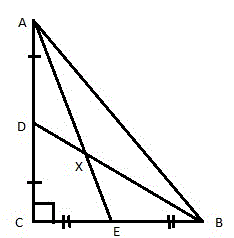
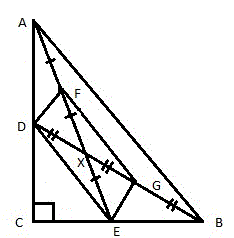
Рассмотрим прямоугольный треугольник ABC. Проведем две медианы AE и BD, которые пересекаются в точке X (рис. 2).

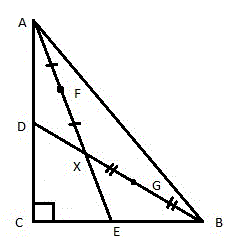
Середины отрезков AX и BX обозначим, соответственно, буквами F и G (рисунок 3).

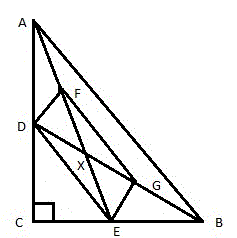
Соединим между собой точки (D, F, G и E) и получим четырёхугольник DFGE (рис. 4).

Сторона DE этого четырёхугольника будет средней линией треугольника ABC. Согласно определению: отрезок, соединяющий середины двух сторон треугольника, является его средней линией. При этом по свойству средняя линия параллельна не пересекающейся с ней стороне и равна половине этой стороны, то есть.
DE || AB и DE = AB / 2.

Аналогично сторона FG треугольника AXB будет его средней линией.
FG || AB и FG = AB / 2

Отсюда следует, что отрезки DE и FG являются параллельными и равными. Следовательно, четырехугольник DFGE – параллелограмм (по признаку параллелограмма).

Так как диагонали параллелограмма в точке пересечения делятся пополам, то
FX=XE, GX=XD

Так как AF = FX (по построению), то и AF = FX = XE, аналогично DX = XG = GB.

Получается, что точка X делит обе медианы AE и BD в соотношении 2 к 1 считая от вершины треугольника.

Аналогично, мы сможем доказать, что точка пересечения 3-ей медианы, проведенной из прямого угла к гипотенузе, с медианой AE (или BD) будет делить ее в соотношении 2 к 1, считая от вершины. То есть наша 3-я медиана также пройдет через точку X. Отсюда следует, что все 3 наши медианы пересекаются в одной точке.

Что и требовалось доказать.

Второе свойство

Доказать, что медиана, проведённая с вершины прямого угла к гипотенузе, равна половине гипотенузы.

Доказательство:

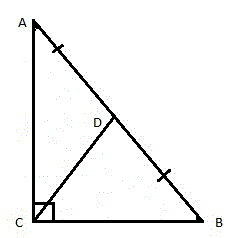
Чтобы доказать это свойство рассмотрим прямоугольный треугольник ABC и проведём медиану к гипотенузе. Точку ее пересечения с гипотенузой обозначим буквой D (рис. 6).

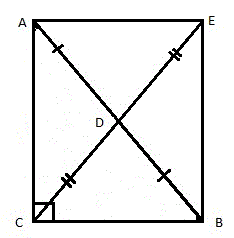
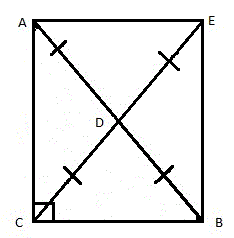
Отразим симметрично наш треугольник ABC относительно отрезка AB (рисунок 7). В результате получим четырёхугольник AEBC, в котором AD=DB (поскольку CD медиана к стороне AB) и CD=DE (по построению). То есть диагонали четырехугольника AEBC пересекаются и точкой пересечения делятся пополам. Отсюда следует, что AEBC является параллелограммом (по признаку параллелограмма).

Один из признаков прямоугольника говорит о том, что параллелограмм является прямоугольником, если хотя бы один из его углов прямой. Поскольку ∠ACB прямой (по построению), то AEBC — прямоугольник.

Поскольку диагонали прямоугольника равны и в точке пересечения делятся пополам (свойство прямоугольника), то AB = CE и AD = DB = CD = DE.

Так как AB = AD + DB, AD = BD и СD = AD = BD, то получается, что медиана AD, проведенная к гипотенузе AB равна половине ее длины.

Что и требовалось доказать.

Третье свойство

Доказать, что медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Доказательство:

Опишем вокруг прямоугольного треугольника ABC окружность.

Поскольку точка C уже лежит на окружности, то для того, чтобы доказать, что медиана CM является радиусом, нам надо доказать, что точка M – центр описанной окружности (т.е. равноудалена от нее).

Так как медиана делит отрезок пополам, а медиана проведенная к гипотенузе равна ее половине (согласно доказанному выше свойству), то точка M будет равноудалена от всех вершин треугольника, которые в свою очередь касаются окружности (рисунок 8).

Отсюда следует, что окружность, описанная вокруг прямоугольного треугольника ABC будет иметь центр на середине гипотенузы (в точке M), а медиана CM будет радиусом описанной окружности.

Что и требовалось доказать.

Понравилась статья, расскажите о ней друзьям:

Видео:ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

Медиана, проведенная к гипотенузе

Определим и докажем, чему равна медиана прямоугольного треугольника, проведенная к гипотенузе.

Медиана, проведенная к гипотенузе, равна половине гипотенузы.

Дано: ∆ ABC, ∠ BCA=90º

Доказать: медиана, проведенная к гипотенузе, равна половине гипотенузы.

1) В прямоугольном треугольнике АВС из вершины прямого угла С проведем к гипотенузе AB отрезок CO так, чтобы CO=OA.

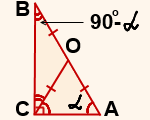
2) ∆ AOC — равнобедренный с основанием AC (по определению равнобедренного треугольника).

Значит, у него углы при основании равны: ∠ OAC = ∠ OCA=α.

3) Так как сумма острых углов прямоугольного треугольника равна 90º, то в треугольнике ABC ∠ B=90º- α.

4) Так как ∠ BCA=90º (по условию), то ∠ BCO=90º- ∠ OCA=90º-α.

5) Рассмотрим треугольник BOC.

∠ BCO=90º-α, ∠ B=90º- α, следовательно, ∠ BCO= ∠ B.

Значит, треугольник BOC — равнобедренный с основанием BC (по признаку равнобедренного треугольника).

6) Так как CO=OA (по построению) и BO=CO (по доказанному), то CO=OA=BO, AB=OA+BO=2∙OA=2∙CO.

Таким образом, точка O — середина гипотенузы AB, отрезок CO соединяет вершину треугольника с серединой противолежащей стороны, значит, CO — медиана, проведенная к гипотенузе, и она равна половине гипотенузы:

Что и требовалось доказать.

Этот способ может быть использован для доказательства свойства медианы прямоугольного треугольника в 7 классе, поскольку опирается только на материал, уже знакомый к моменту изучения данной темы.

Еще один способ доказательства свойства медианы, проведенной к гипотенузе, рассмотрим в следующий раз.

Видео:8. Медиана треугольника и её свойства.Скачать

Определение и свойства медианы прямоугольного треугольника

В данной статье мы рассмотрим определение и свойства медианы прямоугольного треугольника, проведенной к гипотенузе. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Определение медианы прямоугольного треугольника

Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми ( Свойства медианы прямоугольного треугольника

Свойство 1

Медиана (AD) в прямоугольном треугольнике, проведенная из вершины прямого угла (∠BAC) к гипотенузе (BC), равна половине гипотенузы.

BC = 2AD
AD = BD = DC

Следствие: Если медиана равняется половине стороны, к которой она проведена, то данная сторона является гипотенузой, а треугольник – прямоугольным.

Свойство 2

Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.

Для нашего треугольника (см. рисунок выше):

Это следует из теоремы Пифагора и Свойства 1.

Свойство 3

Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу описанной вокруг треугольника окружности.

Т.е. BO – это одновременно и медиана, и радиус.

Примечание: К прямоугольному треугольнику также применимы общие свойства медианы, независимо от вида треугольника.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Пример задачи

Длина медианы, проведенной в гипотенузе прямоугольного треугольника, составляет 10 см. А один из катетов равен 12 см. Найдите периметр треугольника.

Решение
Гипотенуза треугольника, как следует из Свойства 1, в два раза больше медианы. Т.е. она равняется: 10 см ⋅ 2 = 20 см.

Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b 2 = с 2 – a 2 = 20 2 – 12 2 = 256.
Следовательно, b = 16 см.

Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:
P_△ = 12 см + 16 см + 20 см = 48 см.