Доказать треугольник abc amc

§ 16. Сумма углов треугольника

Треугольник — ключевая фигура планиметрии. Мир треугольников разнообразен. Но всем им присуще свойство, которое раскрывает следующая теорема.

Сумма углов треугольника равна 180° .

Рассмотрим произвольный треугольник ABC . Требуется доказать, что ∠ A + ∠ B + ∠ C = 180°.

Через вершину B проведём прямую a , параллельную прямой AC (рис. 243). Имеем: ∠ A и ∠ 1 равны как накрест лежащие при параллельных прямых a и AC и секущей AB . Аналогично доказываем, что ∠ C = ∠ 3. Но углы 1, 2, 3 составляют развёрнутый угол с вершиной B . Следовательно, ∠ A + ∠ ABC + ∠ C = ∠ 1 + ∠ 2 + ∠ 3 = 180°.

Среди углов треугольника хотя бы два угла острые.

Докажите это следствие самостоятельно.

Из этого следствия вытекает, что угол при основании равнобедренного треугольника всегда острый.

Внешним углом треугольника называют угол, смежный с углом этого треугольника.

На рисунке 244 углы 1, 2, 3 являются внешними углами треугольника ABC .

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

На рисунке 244 углы 1, 2 и 3 — внешние углы треугольника АВС . Надо доказать, что ∠ 1 = ∠ 5 + ∠ 6, ∠ 2 = ∠ 4 + ∠ 6, ∠ 3 = ∠ 4 + ∠ 5.

Докажем, например, первое из этих трёх равенств (остальные равенства доказывают аналогично).

По свойству смежных углов ∠ 1 + ∠ 4 = 180°. По теореме о сумме углов треугольника ∠ 4 + ∠ 5 + ∠ 6 = 180°. Тогда ∠ 1 + ∠ 4 = ∠ 4 + ∠ 5 + ∠ 6, отсюда ∠ 1 = ∠ 5 + ∠ 6.

Внешний угол треугольника больше каждого из углов треугольника, не смежных с ним.

Докажите это следствие самостоятельно.

Каждая сторона треугольника меньше суммы двух других его сторон.

Рассмотрим треугольник ABC (рис. 245). Надо доказать, что: 1) AB AC + CB ; 2) AC AB + BC ; 3) BC BA + AC .

Докажем первое из этих неравенств (два других доказывают аналогично).

Пусть доказываемое неравенство неверно. Тогда AB > AC + CB или AB = AC + CB .

1) Пусть AB > AC + CB . Тогда на стороне AB можно отметить точки C 1 и C 2 такие, что AC = AC 1 и BC = BC 2 . Поскольку мы предположили, что AB > AC + CB , то AB > AC 1 + BC 2 . Следовательно, отрезки AC 1 и BC 2 не имеют общих точек (см. рис. 245).

Углы AC 1 C и BC 2 C являются острыми как углы при основании равнобедренных треугольников AC 1 C и BC 2 C соответственно. Тогда углы 1 и 2 являются тупыми как углы, смежные с острыми. Получили противоречие: в треугольнике С 1 СС 2 два тупых угла.

2) Рассуждая аналогично, можно показать (сделайте это самостоятельно), что равенство AB = AC + CB тоже приводит к противоречию.

Из доказанной теоремы следует, что если длина одного из трёх данных отрезков не меньше суммы длин двух других, то эти отрезки не могут служить сторонами треугольника (рис. 246).

В § 23 вы узнаете, что если любой из трёх данных отрезков меньше суммы двух других, то эти отрезки могут служить сторонами треугольника.

Вы уже знаете, что в треугольнике против равных сторон лежат равные углы, и наоборот, против равных углов лежат равные стороны (§ 9, 10). Эти свойства дополняет следующая теорема.

В треугольнике против большей стороны лежит больший угол и, наоборот, против большего угла лежит бóльшая сторона.

1) Рассмотрим треугольник ABC , у которого AB > BC . Надо доказать, что ∠ ACB > ∠ A (рис. 247).

Поскольку AB > BC , то на стороне AB найдётся такая точка M , что BM = BC . Получили равнобедренный треугольник MBC , в котором ∠ BMC = ∠ BCM .

Так как угол BMC — внешний угол треугольника AMC , то ∠ BMC > ∠ A . Следующая «цепочка» доказывает первую часть теоремы:

∠ ACB > ∠ MCB = ∠ BMC > ∠ A .

2) Рассмотрим треугольник ABC , у которого ∠ C > ∠ A . Надо доказать, что AB > BC .

Поскольку ∠ ACB > ∠ A , то угол ACB можно разделить на два угла ACM и MCB так, что ∠ ACM = ∠ A (рис. 248). Тогда треугольник AMC — равнобедренный с равными сторонами MA и MC .

Для стороны BC запишем неравенство треугольника: MB + MC > BC . Учитывая, что MA = MC и MB + MA = AB , получим: AB > BC .

Заметим, что вторую часть теоремы 16.4 можно доказать методом от противного: предположить, что BC ≥ AB , а далее воспользоваться уже доказанной первой частью теоремы. Проведите это доказательство самостоятельно.

Задача. Медиана CM треугольника ABC равна половине стороны AB . Докажите, что треугольник ABC — прямоугольный.

Решение. По условию AM = CM (рис. 249). Тогда в треугольнике AMC углы A и ACM равны.

По условию BM = CM , и в треугольнике BMC углы B и BCM равны.

В треугольнике ACB имеем: ∠ A + ∠ B + + ∠ ACB = 180°. Учитывая, что ∠ A = ∠ ACM и ∠ B = ∠ BCM , получаем: ∠ ACM + ∠ BCM + + ∠ ACB = 180°. Так как ∠ ACM + ∠ BCM = ∠ ACB , то 2 ∠ ACB = 180°. Тогда ∠ ACB = 90°.

Следовательно, треугольник ABC — прямоугольный.

1. Чему равна сумма углов треугольника?
2. Какое наименьшее количество острых углов есть в любом треугольнике?
3. Какой угол называют внешним углом треугольника?
4. Как связаны внешний угол треугольника и два угла треугольника, не смежные с ним?
5. Сравните внешний угол треугольника с углом треугольника, не смежным с ним.
6. Сформулируйте теорему о неравенстве треугольника.
7. Сформулируйте теорему о соотношении между сторонами и углами треугольника.

357. Найдите угол треугольника, если два других его угла равны 35° и 96°.

358. Один из углов треугольника в 3 раза меньше другого угла и на 35° меньше третьего. Найдите углы треугольника.

359. Найдите углы треугольника, если их градусные меры относятся как 2 : 3 : 7.

360. Найдите углы равностороннего треугольника.

361. Найдите углы равнобедренного прямоугольного треугольника.

362. Угол при основании равнобедренного треугольника равен 63°. Найдите угол при вершине этого треугольника.

363. Найдите углы при основании равнобедренного треугольника, если угол при вершине равен 104°.

364. Найдите углы равнобедренного треугольника, если угол при вершине в 4 раза больше угла при основании.

365. Найдите углы равнобедренного треугольника, если угол при основании на 48° меньше угла при вершине.

366. Найдите углы равнобедренного треугольника, если один из них равен: 1) 110°; 2) 50°. Сколько решений имеет задача?

367. Найдите углы равнобедренного треугольника, если один из них равен: 1) 42°; 2) 94°. Сколько решений имеет задача?

368. Могут ли стороны треугольника быть равными:

1) 6 см, 5 см, 12 см; 2) 6 см, 5 см, 11 см?

369. В треугольнике ABC известно, что ∠ C = 90°, AK — биссектриса, ∠ BAK = 18°. Найдите углы AKC и ABC .

370. В треугольнике ABC известно, что AB = BC , CK — биссектриса, ∠ A = 66°. Найдите ∠ AKC .

371. Биссектрисы AK и CM треугольника ABC пересекаются в точке O , ∠ BAC = 116°, ∠ BCA = 34°. Найдите ∠ AOC .

372. В равнобедренном треугольнике ABC с углом при вершине B , равным 36°, провели биссектрису AD . Докажите, что треугольники ADB и CAD — равнобедренные.

373. В треугольнике ABC провели биссектрису BF . Найдите угол C , если ∠ A = 39°, ∠ AFB = 78°.

374. Докажите, что если один из углов треугольника равен сумме двух других углов, то этот треугольник — прямоугольный.

375. На рисунке 250 укажите внешние углы:

1) при вершинах E и F треугольника MEF ;

2) при вершине E треугольника MKE .

376. На рисунке 251 укажите треугольники, для которых внешним углом является: 1) угол AMB ; 2) угол BMD .

377. Один из внешних углов треугольника равен 75°. Чему равны:

1) угол треугольника при этой вершине;

2) сумма двух углов треугольника, не смежных с ним?

378. Может ли внешний угол треугольника быть меньше смежного с ним угла треугольника? В случае положительного ответа укажите вид треугольника.

379. Определите вид треугольника, если один из его внешних углов равен смежному с ним углу треугольника.

380. Один из внешних углов треугольника равен 136°, а один из углов треугольника, не смежный с ним, — 61°. Найдите второй угол треугольника, не смежный с данным внешним.

381. Один из внешних углов треугольника равен 154°. Найдите углы треугольника, не смежные с ним, если один из этих углов на 28° больше другого.

382. Один из внешних углов треугольника равен 98°. Найдите углы треугольника, не смежные с ним, если один из этих углов в 6 раз меньше другого.

383. Найдите углы равнобедренного треугольника, если внешний угол при его вершине равен 38°.

384. Сравните углы треугольника ABC , если:

1) AB > AC > BC ; 2) AB = BC , BC > AC .

385. В треугольнике ABC известно, что ∠ A = 34°, ∠ B = 28°. Сравните стороны AB , BC и AC .

386. Сравните стороны треугольника ABC , если:

1) ∠ C > ∠ A > ∠ B ; 2) ∠ B > ∠ C , ∠ A = ∠ B .

387. Докажите, что если два угла одного треугольника равны соответственно двум углам другого треугольника, то и третьи углы этих треугольников равны.

388. Найдите углы равнобедренного треугольника, если один из его внешних углов равен: 1) 54°; 2) 112°. Сколько решений имеет задача?

389. Внешний угол равнобедренного треугольника равен 130°. Найдите углы треугольника. Сколько решений имеет задача?

390. Периметр треугольника равен 30 см. Может ли одна из его сторон быть равной: 1) 20 см; 2) 15 см?

391. Длины двух сторон треугольника равны 7 и 9 см. Может ли периметр этого треугольника быть равным: 1) 20 см; 2) 32 см; 3) 18 см?

392. Существует ли треугольник, одна из сторон которого на 2 см меньше второй и на 6 см меньше третьей, а периметр равен 20 см?

393. Биссектрисы углов при основании AC равнобедренного треугольника ABC пересекаются в точке O . Докажите, что угол AOC равен внешнему углу треугольника ABC при вершине A .

394. На рисунке 252 BC ‖ AD , ∠ A = 25°, ∠ B = 55°. Найдите угол CMD .

395. Отрезок BK — биссектриса равнобедренного треугольника ABC с основанием BC , ∠ AKB = 105°. Найдите углы треугольника ABC .

396. На стороне AB треугольника ABC отметили точку D так, что BD = BC , ∠ ACD = 15°, ∠ DCB = 40°. Найдите углы треугольника ABC .

397. На сторонах треугольника ABC (рис. 253) отметили точки E и F так, что ∠ 1 = ∠ 2. Докажите, что ∠ 3 = ∠ 4.

398. На рисунке 254 BC ‖ AD , ∠ B = 100°, ∠ ACD = 95°, ∠ D = 45°. Докажите, что AB = BC .

399. Через вершину C треугольника ABC проведена прямая, параллельная биссектрисе AM треугольника и пересекающая прямую AB в точке K . Найдите углы треугольника AKC , если ∠ BAC = 70°.

400. В треугольнике ABC биссектрисы углов A и C пересекаются в точке O . Найдите ∠ AOC , если ∠ B = 100°.

401. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна его основанию.

402. Докажите, что если биссектриса внешнего угла треугольника параллельна его стороне, то этот треугольник равнобедренный.

403. Угол при основании AC равнобедренного треугольника ABC в 2 раза больше угла при вершине, AM — биссектриса треугольника. Докажите, что BM = AC .

404. Треугольник ABC равнобедренный с основанием AC . На стороне BC отметили точку M так, что BM = AM = AC . Найдите углы треугольника ABC .

405. Докажите, что в любом треугольнике существует угол: 1) не меньше 60°; 2) не больше 60°.

406. Определите вид треугольника, если:

1) один из его углов больше суммы двух других;

2) любой из его углов меньше суммы двух других.

407. Определите вид треугольника, если сумма любых двух его углов больше 90°.

408. В треугольнике ABC угол B — тупой. На продолжении стороны AB за точку A отметили произвольную точку D . Докажите, что CD > AC .

409. В треугольнике ABC известно, что ∠ C > 90°. На стороне BC отметили произвольную точку D . Докажите, что AD > AC .

410. Существует ли треугольник, две биссектрисы которого перпендикулярны?

411. Существует ли треугольник, в котором одна биссектриса делит пополам другую биссектрису?

412. Найдите углы треугольника ABC , если биссектриса угла B разбивает его на два равнобедренных треугольника.

413. Три точки A , B и C таковы, что выполняется равенство AB = AC + CB . Докажите, что точка C является внутренней точкой отрезка AB .

414. На прямой m (рис. 255) найдите такую точку C , чтобы сумма расстояний от неё до точек A и B была наименьшей. Ответ обоснуйте.

415. Одна сторона треугольника равна 2,8 см, а вторая — 0,6 см. Найдите третью сторону этого треугольника, если её длина, выраженная в сантиметрах, равна целому числу.

416. В треугольнике ABC известно, что ∠ A = α , биссектрисы внешних углов при вершинах B и C пересекаются в точке O . Найдите ∠ BOC .

417. Отрезок AM — медиана треугольника ABC , ∠ CAM > ∠ BAM . Докажите, что AB > AC .

418. На боковых сторонах AB и BC равнобедренного треугольника ABC отметили соответственно точки E и F так, что AC = AF = EF = BE . Найдите углы треугольника ABC .

419. В треугольнике ABC известно, что AB = 2 см, ∠ A = 60°, ∠ B = 70°. На стороне AC отметили точку D так, что AD = 1 см. Найдите углы треугольника BDC .

420. Докажите, что сумма длин двух сторон треугольника больше удвоенной длины медианы, проведённой к третьей стороне.

Упражнения для повторения

421. На прямой отметили точки A , B и C так, что точка B лежит между точками A и C и BC = 2 AB . На отрезке BC отметили точку D так, что BD : DC = 3 : 7. Найдите расстояние между серединами отрезков AB и CD , если отрезок CD на 16 см длиннее отрезка BD .

422. На медиане BM треугольника ABC отметили точку O так, что ∠ OAC = ∠ OCA . Докажите, что треугольник ABC — равнобедренный.

Наблюдайте, рисуйте, конструируйте, фантазируйте

423. Существует ли шестиугольник, у которого никакие две диагонали не имеют общих точек, отличных от вершин?

Видео:Геометрия На стороне AB треугольника ABC отметили точку M так что угол AMC = φ Найдите отрезок CMСкачать

Урок геометрии по теме «Перпендикулярность прямой и плоскости». 10-й класс

Разделы: Математика

Класс: 10

Цели:

1. закрепить вопросы теории по теме «Перпендикулярность прямой и плоскости»;
2. вырабатывать навыки применения теоретических знаний к решению типовых задач на перпендикулярность прямой и плоскости.

План:

1. Теоретический опрос.
   1. Доказательство изученных теорем у доски.
   2. Фронтальный опрос.
   3. Презентации учащихся по данной теме.
2. Решение задач.
   1. Решение устных задач по готовым чертежам.
   2. Решение письменных задач (по группам).
   3. Самостоятельная работа с индивидуальным заданием.
3. Итог урока. Задание на дом.

Ход урока

I. Теоретический опрос (4 ученика у доски)

1) доказать лемму о 2-ух параллельных прямых, одна из которых перпендикулярна к третьей;
2) доказать теорему о 2-ух параллельных прямых, одна из которых перпендикулярна к плоскости;
3) доказать обратную теорему о параллельности 2-ух прямых, перпендикулярных к плоскости;
4) доказать признак перпендикулярности прямой и плоскости.

Пока ученики готовятся у доски к ответу, с классом проводится фронтальный опрос.
(С помощью мультимедиапроектора на экране появляются вопросы (Приложение 1), и ученики отвечают на них)

1. Закончить предложение:

а) две прямые в пространстве называются перпендикулярными, если… (угол между ними равен 90°)
б) прямая называется перпендикулярной к плоскости, если… (она перпендикулярна к любой прямой, лежащей в этой плоскости)
в) если две прямые перпендикулярны к плоскости, то они… (параллельны)
г) если плоскость перпендикулярна к одной из двух параллельных прямых, то она… (перпендикулярна и к другой прямой)
д) если две плоскости перпендикулярны к одной прямой, то они… (параллельны)

2. Дан параллелепипед

б) Определите взаимное расположение:
1) прямой CC₁ и плоскости (DСВ) (ответ: они перпендикулярны)
2) прямой D₁C₁ и плоскости (DCB) (ответ: они параллельны)

Далее выслушиваются ответы учеников у доски с дополнениями и исправлениями по необходимости. Затем рассматриваются презентации по данной теме, подготовленные рядом учеников в качестве зачётных работ (Приложение 2, Приложение 3, Приложение 4).
(Накануне изучения каждой темы учащимся предлагается такой вариант зачёта)

II. Решение задач.

1. Решение задач по готовым чертежам (Устно)

№1

Дано: ∆ ABC — прямоугольный; AM ⊥ AC; M ∉ (ABC)
Доказать: AC ⊥ (AMB)
Доказательство: Т.к. AC ⊥ AB и AC ⊥ AM, а AM ⋂ AB, т.е. АМ и АВ лежат в плоскости (АМВ), то AC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

№2

Дано: ВМDC — прямоугольник, M ∉ (ABC), MB ⊥ AB
Доказать: CD ⊥ (ABC)
Доказательство: MB ⊥ BC, т.к. ВМDC – прямоугольник, MB ⊥ AB по условию, BC ⋂ AB, т.е. ВС и АВ лежат в плоскости (АВС) ⇒ MB ⊥ (ABC) по признаку перпендикулярности прямой и плоскости. СD ∥ МВ по свойству сторон прямоугольника ⇒ CD ⊥ (ABC) по теореме о двух параллельных прямых, одна из которых перпендикулярна к плоскости (то и другая прямая перпендикулярна к этой плоскости).
Ч.т.д.

№3

Дано: АВСD – прямоугольник, M ∉ (ABC), MB ⊥ BC
Доказать: AD ⊥ AM
Доказательство:
1) ∠ABC = 90°, т.к. АВСD – прямоугольник ⇒ BC ⊥ AB, BS ⊥ MB по условию, MB ⋂ AB = B, т.е. МВ и АВ лежат в плоскости (АМВ) ⇒ BC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
2) BC ∥ AD (по свойству сторон прямоугольника) ⇒ AD ⊥ (AMB) по теореме о двух параллельных прямых, одна из которых перпендикулярна плоскости (то и другая прямая перпендикулярна к этой плоскости).
3) Т.к. AD ⊥ (AMB) ⇒ AD ⊥ AM по определению прямой, перпендикулярной плоскости.
Ч.т.д.

№4

Дано: АВСD – параллелограмм, M ∉ (ABC), МВ = МD, МА = МС
Доказать: MO ⊥ (ABC)
Доказательство:
1) Т.к. О – точка пересечения диагоналей параллелограмма, то АО = СО и ВО = DO. ∆ BMD — равнобедренный, т. к. ВМ = МD по условию, значит МО — медиана и высота, т.е. MO ⊥ BD.
2) Аналогично доказывается в ∆ AMC: MO ⊥ AC.
3) Итак, MO ⊥ BD и MO ⊥ AC. а ВD и АС – пересекающиеся прямые, лежащие в плоскости (АВС) ⇒ MO ⊥ (ABC) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

(Устные ответы к каждой задаче требуется обосновывать, проговаривая всякий раз формулировки применяемых теорем)

2. Решение письменных задач

Класс делится на три группы (например, по рядам), и каждой группе даётся задача с последующей проверкой решения у доски.

№1.2 (№125 учебника)

Через точки P и Q прямой РQ проведены прямые, перпендикулярные к плоскости α и пересекающие её соответственно в точках P₁ и Q₁. Найдите P₁Q₁, если PQ = 15 cм; PP₁ = 21,5 cм; QQ₁ = 33,5 cм.
Решение:

1) PP₁ ⊥ α и QQ₁ ⊥ α по условию ⇒ PP₁ ∥ QQ₁ (обосновать);
2) PP₁ и QQ₁ определяют некоторую плоскость β, α ⋂ β = P₁Q₁;
3) PP₁Q₁Q — трапеция с основаниями PP₁ и QQ₁, проведём PK ∥ P₁Q₁;
4) QK = 33,5 — 21,5 = 12 (см)

P1Q1 = PK =

= 9 см.

№2.2

1) ∆ ABD: ∠BAD = 90°; АD = BC = 8 см;

ВD =

см;

2) ∆ DD₁B: ∠D₁DB = 90°;

DD1 =

= 12 см;

3) SBB1D1D = BD ∙ DD1 =

см 2 .

Ответ:

см 2 .

№3.2

Отрезок МН пересекает плоскость α в точке К. Из концов отрезка проведены прямые МЕ и НР, перпендикулярные к плоскости α. НР = 4 см; МЕ = 12 см; НК = 5 см. Найдите отрезок РЕ.
Решение:

1) Т.к. прямые МЕ и НР перпендикулярны к плоскости α, то МЕ ∥ НР (обосновать) и через них проходит некоторая плоскость β. α ⋂ β = EP;
2)МЕ ⊥ EP; НР ⊥ EP(обосновать), т.е. ∠MEK = ∠HPK = 90°;

3) ∆ HPK: KP =

= 3 см;

4) ∠EMK = ∠PHK (накрест лежащие для параллельных прямых МЕ и НР и секущей МН),

тогда ∆ MEK ∆ HPK по двум углам и

; т.е.

⇒ EK =

= 9 см,

РЕ = РК + КЕ, РЕ = 3 + 9 = 12 см.

Ответ: РЕ = 12 см.

3. Самостоятельная работа (направлена на проверку усвоения материала по данной теме)

1) AA₁ ⊥ AB, AA₁ ⊥ AD, а AB ⋂ AD = A ⇒ AA₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. AA₁ ∥ BB₁, то BB₁ ⊥ (ABC) ⇒ BB₁ ⊥ BD;
2) ∆ ABD: ∠BAD = 90°. По теореме Пифагора:

BD =

= 20 см;

3) ∆ B₁BD – прямоугольный. По теореме Пифагора:

B1B =

= 15 см.

1) BB₁ ⊥ AB, BB₁ ⊥ BC, а AB ⋂ BC = B ⇒ BB₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. BB₁ ∥ AA₁, то AA₁ ⊥ (ABC) ⇒ AA₁ ⊥ AC;
2) Используя свойство диагоналей ромба, имеем в ∆ AOB: ∠AOB = 90°, BO = ½ BD = 8 см. По теореме Пифагора:

AO =

= 6 см,

AO = ½ AC ⇒ AC = 12 см;
3) ∆ A₁AC – прямоугольный. По теореме Пифагора:

AA1 =

= 5 см.

Индивидуальное задание для более сильных учеников. (Вариант III)

1) Т.к. CD ⊥ (FDC) ⇒ CD ⊥ AC и CD ⊥ BC, т.е. ∆ ADC, ∆ BDC – прямоугольные;
2) ∆ ADC = ∆ BDC (по двум катетам) ⇒ AD = BD, т.е. ∆ ADB – равнобедренный и DM – медиана, а значит и высота; 3) DC ⊥ MC ⇒ MCD – прямоугольный,

тогда MC =

= 9;

4) ∆ ABC – равносторонний, поэтому СМ – медиана и высота, т.е. ∆ MCB – прямоугольный, ∠B = 60°,

sin ∠B =

, тогда

,

а АВ = ВС (по условию).
5) S_{∆ ADB} = ½ DM ∙ AB;

S∆ ADB = ½ ∙ 15 ∙

.

Ответ:

III. Подводятся итоги урока. Задание на дом: повторить теоретический материал по изученной теме, глава II, №130, №131.

Для подготовки к уроку использовались материалы учебника «Геометрия – 10-11» авторов Л.С. Атанасяна, В.Ф. Бутузова и др., методические рекомендации к учебнику «Изучение геометрии в 10-11 классах» авторов С.М. Саакяна, В.Ф. Бутузова, «Поурочные разработки по геометрии» автора В.А. Яровенко.

Видео:№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать

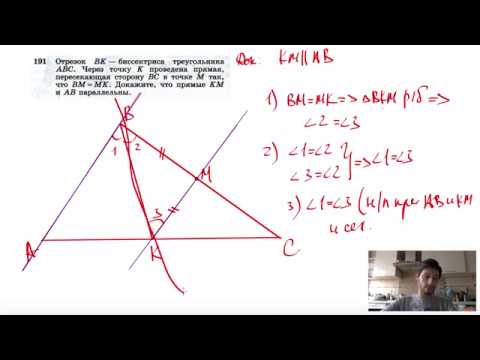
Свойства медианы треугольника. Итоговое повторение курса геометрии 7 – 9 класса

Свойства медианы треугольника

Итоговое повторение курса геометрии 7 – 9 класса

При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме. Предлагаю рассмотреть задачи, которые позволят увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная система задач является эффективным средством повторения, обобщения и систематизации учебного материала в ходе подготовки учащихся к экзамену.

Для сдачи экзамена не лишними будут дополнительные сведения о некоторых элементах треугольника. Рассмотрим свойства медианы треугольника и задачи, при решении которых этими свойствами можно воспользоваться. В предложенных задачах реализуется принцип уровневой дифференциации. Все задачи условно поделены на уровни (уровень указан в скобках после каждого задания).

Вспомним некоторые свойства медианы треугольника

Свойство 1. Докажите, что медиана треугольника ABC, проведённая из вершины A, меньше полусуммы сторон AB и AC.

Отложим на продолжении медианы AM за точку M отрезок MK, равный AM. Тогда в четырёхугольнике ABKC диагонали пересекаются и точкой пересечения делятся пополам. Значит, ABKC — параллелограмм. Применяя неравенство треугольника к треугольнику ABK, получим, что

то, сложив почленно эти три неравенства, получим, что

2AM + BN + CK > AB + BC + AC.

Отсюда следует, что AM + BN + CK > (AB + BC + AC).

Отложим на продолжении медианы AM за точку M отрезок MA1, равный AM. Тогда ABA1C — параллелограмм. Поэтому

BA1 = AC, 2AM = AA1 SDEF’ , то SAED+SBFD>SDEF , следовательно, указанным образом расположить точки невозможно.

так расположить точки нельзя.

Источник: Окружная олимпиада (Москва) , 2008 г, 11 класс

№32 Темы: Удвоение медианы. Ортоцентр и ортотреугольник Сложность:5 + Три точки, лежащие на одной прямой Подобные треугольники Классы: 9,10

В неравнобедренном треугольнике ABC точки H и M – точки пересечения высот и медиан соответственно. Через вершины A , B и C проведены прямые, перпендикулярные прямым AM , BM , CM соответственно. Докажите, что точка пересечения медиан треугольника, образованного проведенными прямыми, лежит на прямой MH .

Решение

Пусть A’B’C’ – треугольник, образованный

проведенными прямыми и G – точка пересечения его

медиан. Мы докажем, что M является серединой отрезка GH . Достроим треугольник BMC до параллелограмма BMCA1 . Отрезок MA1 делит сторону BC пополам, поэтому A1 лежит на прямой AM , причем AM = A1M (поскольку точка M делит медиану в отношении 2:1 ). Кроме того, BA1|| MC A’B’ и CA1|| MB A’C’ , поэтому BA1 и CA1 – высоты треугольника BA’C , значит A1 является ортоцентром треугольника BA’C , и

A’A1 BC . Стороны треугольника BA1M перпендикулярны

сторонам треугольника A’B’C’ соответственно, поэтому эти треугольники подобны, причем соответствующие прямые BC и

AG , содержащие медианы этих треугольников,

перпендикулярны. Значит, прямая A’G совпадает с прямой A’A1 . Пусть G’ – точка, симметричная точке H относительно M . Треугольники AHM и A1G’M симметричны относительно M , поэтому A1G’|| AH BC . Отсюда следует, что G’ лежит на прямой A’G . Аналогично, получаем, что G’ лежит на прямой B’G , то есть G’ совпадает с G .

Источник: Всероссийская олимпиада по математике, 2008 г, 9 класс

Отрабатываем умение: самостоятельно решать задачи.

Свойства медианы. Площадь треугольника

1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.

2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.

3. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна . Найдите площадь треугольника.

4. В треугольнике АВС медианы АD и ВE перпендикулярны, , . Чему равен квадрат третьей стороны?

5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.

6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.

7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.

8. Найдите площадь треугольника, если две его стороны равны 1 и , а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма).

О т в е т: .

1. Одна сторона треугольника равна а, другая – b. Найдите третью сторону, если известно, что она равна медиане, проведенной к ней.

О т в е т: .

2. Основание равнобедренного треугольника , медиана боковой стороны 5. Найдите длины боковых сторон.

3. В равнобедренном треугольнике основание равно , а угол при основании равен 300. Найдите длину медианы, проведенной к боковой стороне.

4. Медианы треугольника равны 5, и . Докажите, что треугольник прямоугольный.

5. Числа , и выражают длины медиан некоторого треугольника. Докажите, что если выполняется равенство , то треугольник является прямоугольным.

Медиана, проведенная к гипотенузе

1. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 3 см и делит прямой угол в отношении 2:1. Найдите меньший катет.

2. АА1, ВВ1, СС1 – медианы треугольника АВС. . Найдите .

3. Медианы треугольника АВС АА1, ВВ1 и СС1 пересекаются в точке О. .см. см. Найдите ВО.

4. Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найдите острые углы треугольника.

О т в е т: 150; 750.

5. В трапеции ABCD углы при основании AD равны 200 и 700, длина отрезка, соединяющего середины оснований, равна 3. Найдите длину отрезка, соединяющего середины диагоналей трапеции.

· , , Ленинградские математические кружки

· , Задачи по планиметрии, Издательство МЦНМО, 2001г

· интернет сайт http://zadachi. ***** Задачи по геометрии

· Всероссийская олимпиада по математике, 2008 год,

· Турнир им. Ломоносова, 2001 год

· Московская математическая регата, 2012/13 г, 8 класс

📹 Видео

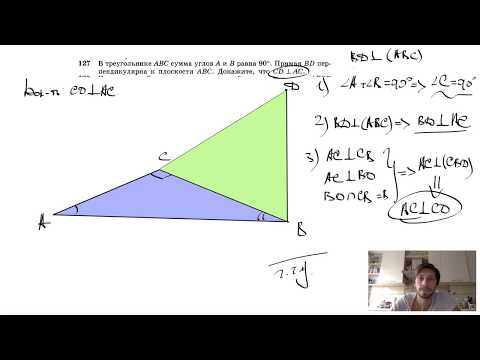
№127. В треугольнике ABC сумма углов A и B равна 90°. Прямая BD перпендикулярна к плоскостиСкачать

№265. В равнобедренном треугольнике ABC с основанием АС проведены биссектриса AF и высота АН.Скачать

№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

№149. Отрезок AD перпендикулярен к плоскости равнобедренного треугольника ABC. Известно,Скачать

№171. В треугольниках ABC и ADC стороны ВС и AD равны и пересекаются в точке О, ∠OAC=∠OCA. ДокажитеСкачать

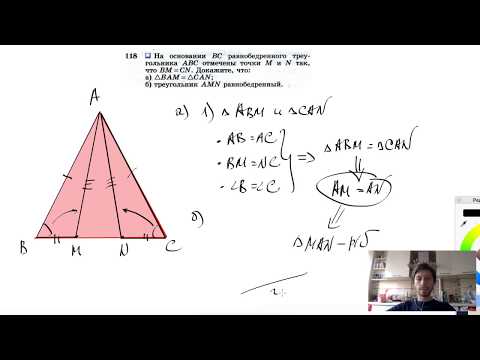
№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать

Математика это не ИсламСкачать

№140. В треугольниках ABC и А1B1С1 медианы ВМ и B1М1 равны, АВ =А1B1, АС=А1С1. Докажите, что ΔABCСкачать

№121. В треугольнике ABC дано: ∠C = 90°, AC = 6 см, ВС = 8 см, СМ — медиана. Через вершину ССкачать

Как доказать, что, если ab+bc+ca=0, то abc представимо в виде m^2·n^3, где a, b, c, m, n — целые?Скачать

В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найти меньший угол треугольника ABCСкачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

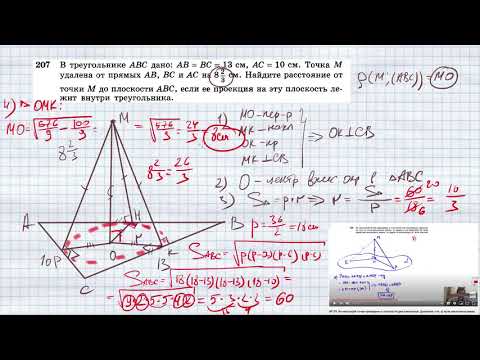
№207. В треугольнике ABC дано: АВ = ВС = 13 см, AС = 10 см. Точка М удалена от прямых АВ, ВС и АС наСкачать

Расчёт углов | Задачи 11-18 | Решение задач | Волчкевич | Уроки геометрии в задачах 7-8Скачать

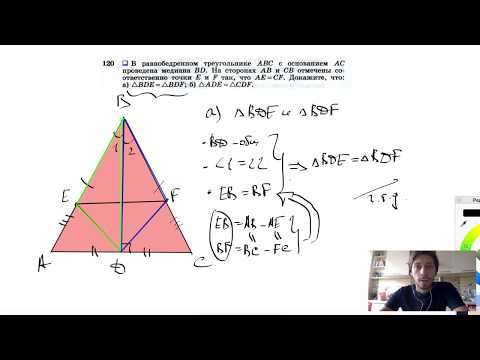
№120. В равнобедренном треугольнике ABC с основанием АС проведена медиана BD. На сторонах АВ и СВСкачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать