Доказать равенство углов в треугольниках

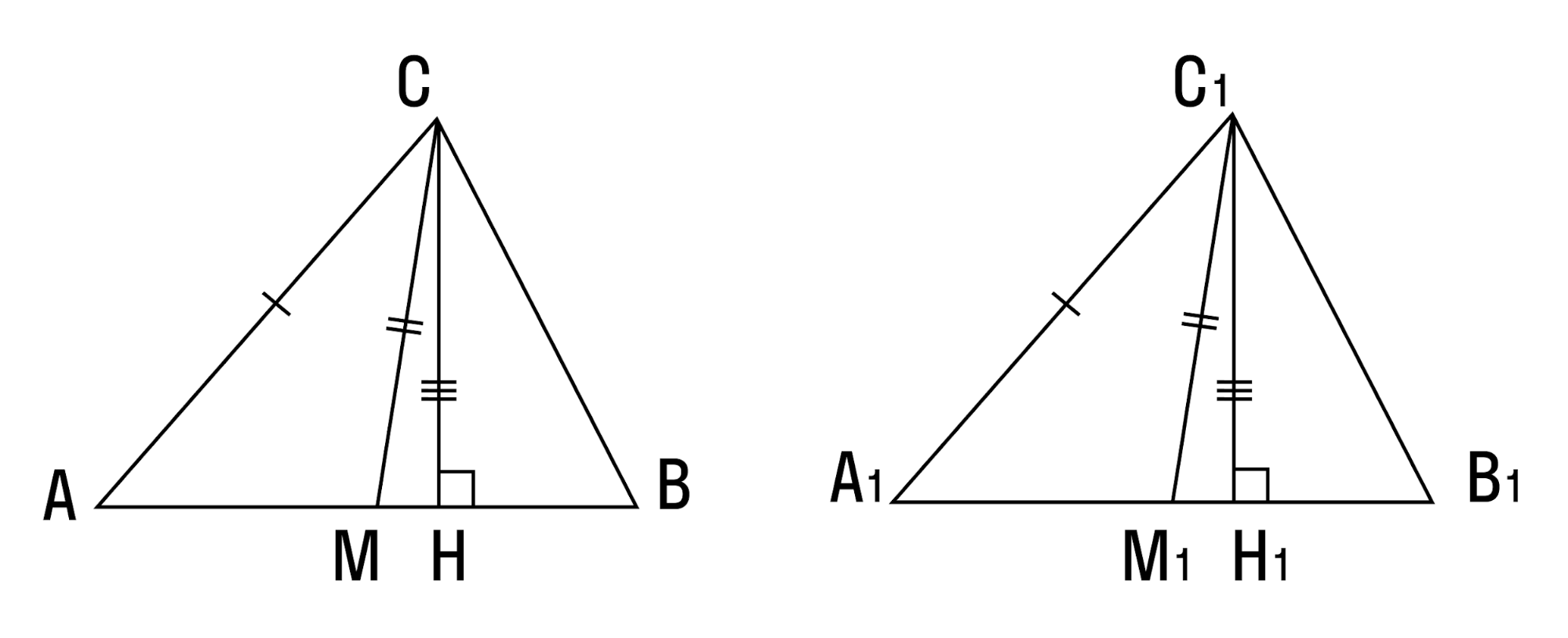
Как доказать, что углы треугольников равны? Рассмотрим возможные варианты.

Углы треугольников могут быть равны в следующих случаях:

1) Угол — общий (один и тот же угол принадлежит одновременно двум различным треугольникам).

3) Углы при основании равнобедренного треугольника равны.

4) Если дана биссектриса треугольника, то исходный угол разделен ею на два равных угла.

5) Если дана высота треугольника, то она образует два прямых (а значит, равных) угла.

6) Угол, смежный с прямым, есть прямой угол (а значит, они равны между собой).

7) Углы, смежные с равными, равны между собой.

8) Соответствующие углы равных треугольников равны между собой.

9) Если к равным углам прибавить равные углы, то получим равные углы.

10) Если из равных углов вычесть равные углы, то получим равные углы.

11) Внутренние накрест лежащие углы при параллельных прямых и секущей равны между собой.

12) Соответственные углы при параллельных прямых и секущей равны между собой.

13) Углы равны по условию.

14) Углы равны по построению.

15) Углы равны по доказанному.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

5 Comments

На вопрос вы так и не ответили. «Как доказать, что углы равны?» а не «В каких случаях углы равны?». Как-то так; информация не полная, а так все отлично.

Равенство углов следует из равенства треугольников. Значит, в большинстве задач, чтобы доказать, что углы равны, нужно доказать равенство треугольников.
Еще можно доказать, что два угла являются углами при основании равнобедренного треугольника, соответственными или внутренними накрест лежащими углами при параллельных прямых и т.д. — об этом сказано выше.

А если в «моём» случае не подходит?

Значит, искать «свой», подходящий вариант.

Спасибо, очень много вариантов! Я уж думала никогда не найду ответ, а тут белая куча ответов! Спасибо!

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Признаки равенства треугольников

О чем эта статья:

Видео:Признаки равенства треугольников. 7 класс.Скачать

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

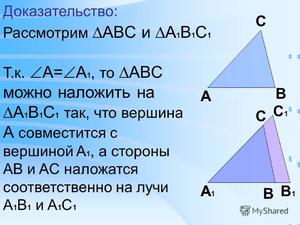
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Видео:Задача на доказательства равенства угловСкачать

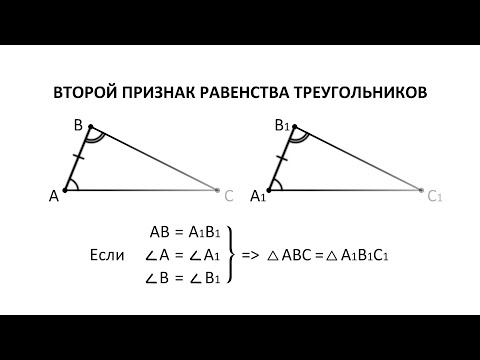
Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

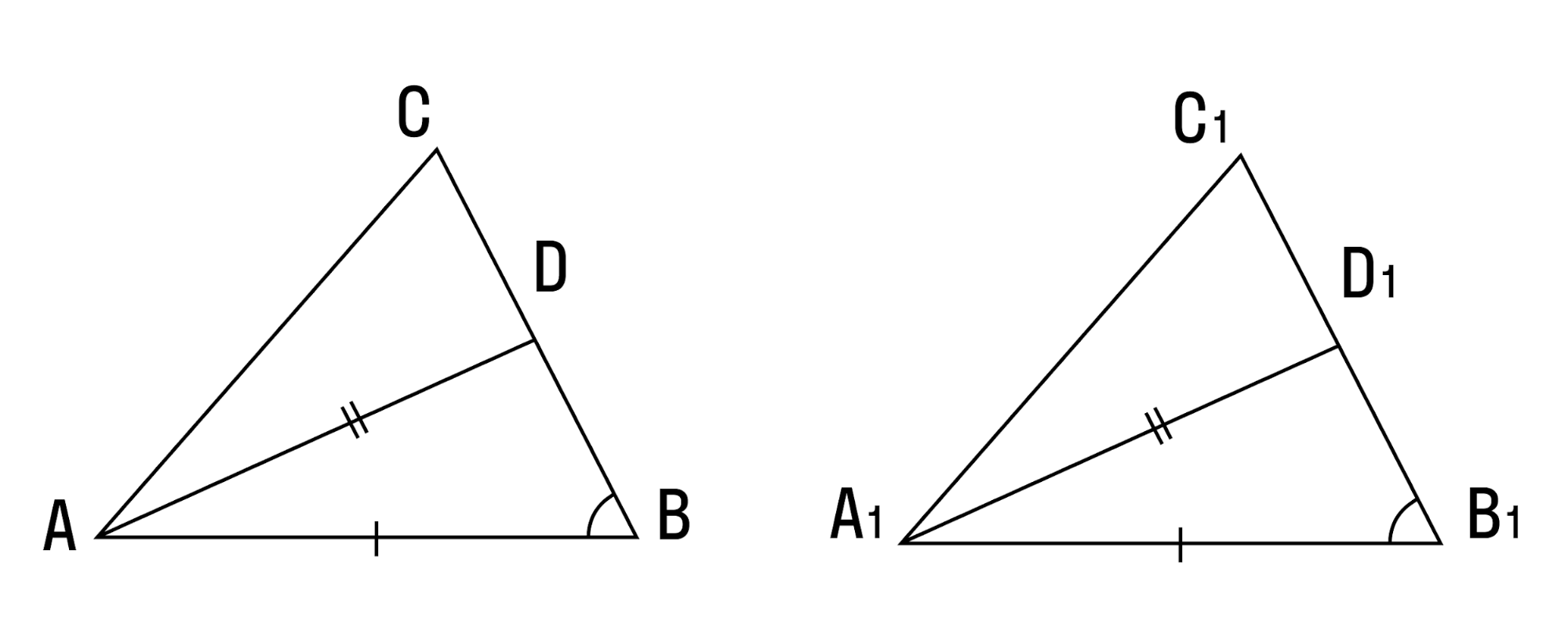
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Видео:Геометрия. 7 класс. Теоремы. Т7. Второй признак равенства треугольников.Скачать

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

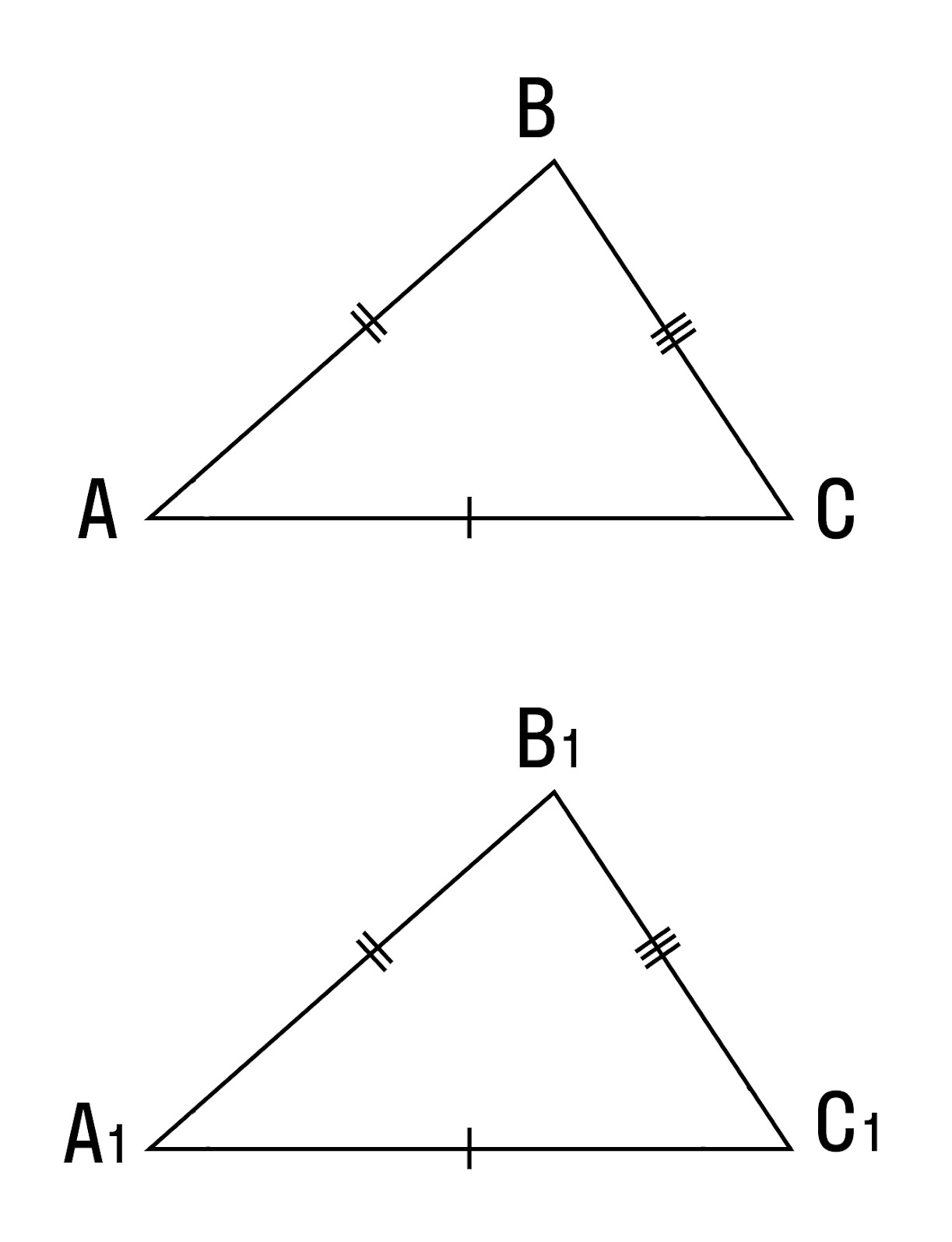
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

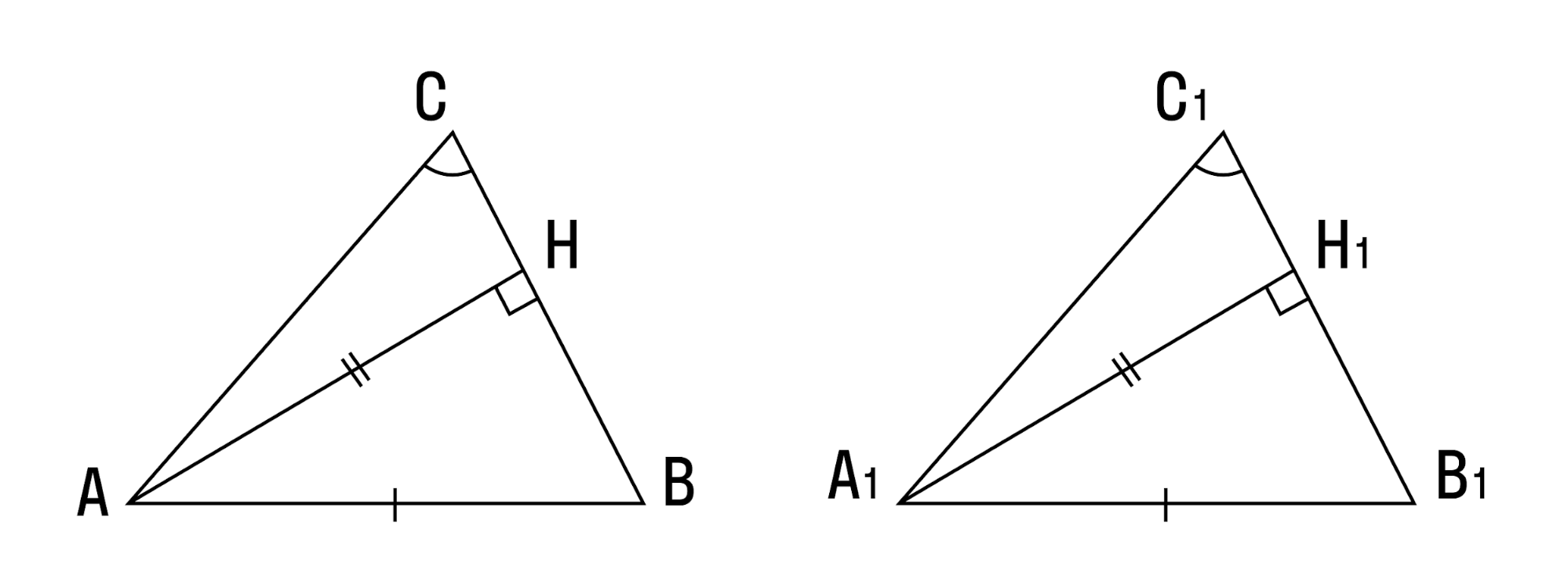
1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
   
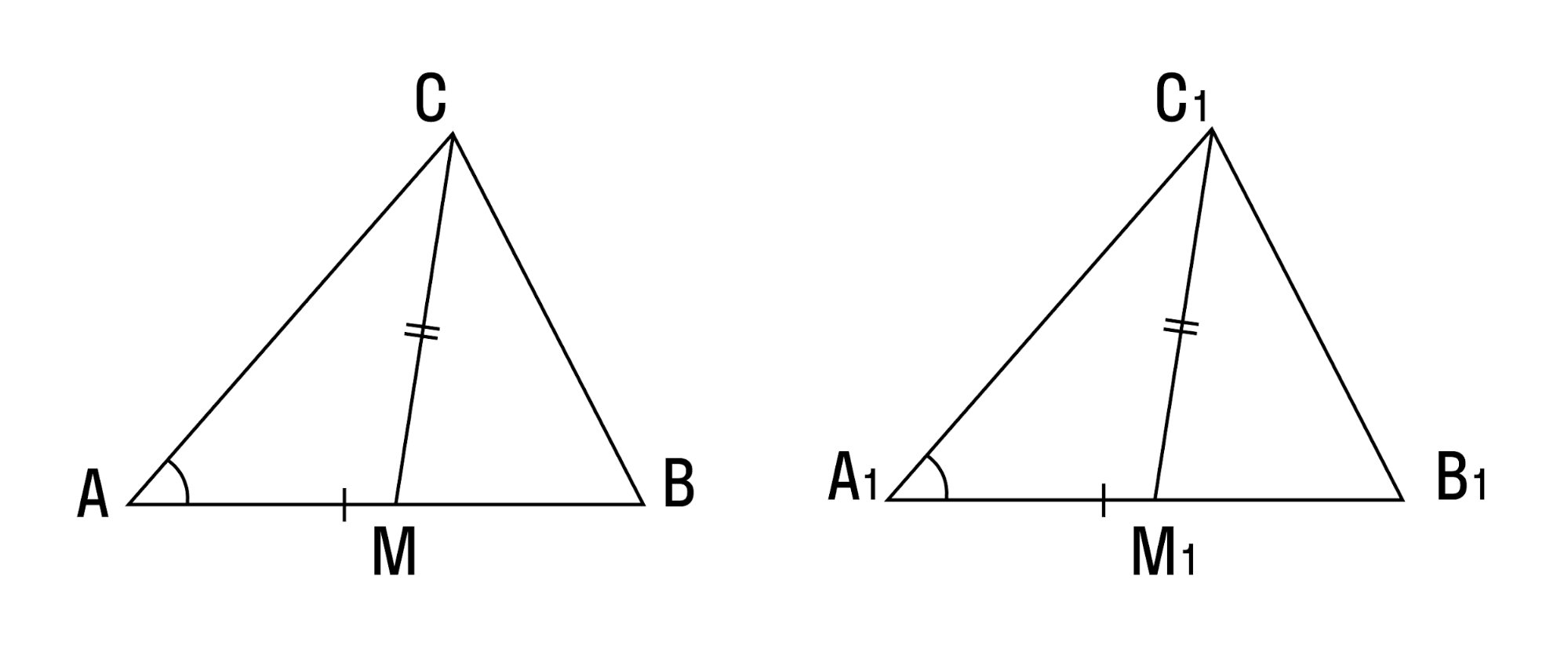
2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
   
3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
   
4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
   
5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
   

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Видео:Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать

Как установить и доказать, что треугольники равны

Геометрия как отдельный предмет начинается у школьников в 7 классе. До этого времени они касаются геометрических задач достаточно лёгкой формы и в основном того, что можно рассмотреть на наглядных примерах: площади комнаты, земельного участка, длины и высоты стен в помещениях, периметра плоских предметов и прочее. В нача ле изучения непосредственно геометрии появляются первые сложности, такие, например, как понятие прямой, так как потрогать руками эту прямую нет возможности. Что касается треугольников -это самый простой вид многоугольников, содержащий всего три угла и три стороны.

Тема треугольников одна из основных важных и больших тем школьной программы в геометрии 7−9 классов. Усвоив её хорошо, возможно решать очень сложные задачи. При этом можно изначально рассматривать совершенно другую геометрическую фигуру, а затем разделить её для удобства на подходящие треугольные части.

Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Как доказать, что треугольники равны

Для работы над доказательством равенства ∆ ABC и ∆A1B1C1 нужно хорошо усвоить признаки равенства фигур и уметь ими пользоваться. Перед изучением признаков необходимо научиться определять равенство сторон и углов простейших многоугольников.

Чтобы доказать, что углы треугольников равны, помогут следующие варианты:

1. ∠ α = ∠ β исходя из построения фигур.
2. Дано в условии задания.
3. При двух параллельных прямых и наличии секущей могут образоваться как внутренние накрест лежащие, так и соответственные ∠ α = ∠ β.
4. Прибавляя (вычитая) к (из) ∠ α = ∠ β равные углы.
5. Всегда сходны вертикальные ∠ α и ∠ β
6. Общий ∠ α, одновременно принадлежащий ∆ MNK и ∆ MNH .
7. Биссектриса делит ∠ α на два равнозначных.
8. Смежный с ∠90° — угол, равный исходному.
9. Смежные равным углам равны.
10. Высота образует два смежных ∠90° .
11. В равнобедренном ∆ MNK при основании ∠ α = ∠ β.
12. В равных ∆ MNK и ∆ SDH соответствующие ∠ α = ∠ β.
13. Доказанное ранее равенство ∆ MNK и ∆ SDH .

Это интересно: Как найти периметр треугольника.

3 признака равенства треугольников

Доказательство равенства ∆ ABC и ∆A1B1C1 очень удобно производить, опираясь на основные признаки тождественности этих простейших многоугольников. Существует три таких признака. Они являются очень важными при решении многих геометрических задач. Стоит рассмотреть каждый.

• I признак. Две стороны и угол между ними ∆ ABC соответственно = двум сторонам и углу ∆ A1B1C1 , следовательно, треугольники равны.
• II признак. Сторона и два прилежащих к ней угла ∆ ABC соответственно = стороне и двум углам ∆ A1B1C1 , => треугольники равны.
• III признак. Если все стороны ∆ ABC соответственно = сторонам ∆ A1B1C1 , то имеющиеся треугольники равны.

Перечисленные выше признаки являются теоремами и доказываются методом наложения одной фигуры на другую, соединения вершин соответственных углов и начала лучей. Доказательства равенства треугольников в 7 классе описаны в очень доступной форме, но сложны в изучении школьниками на практике, так как содержат большое количество элементов, обозначенных заглавными латинскими буквами. Это не совсем привычно для многих учеников на момент начала изучения предмета. Подростки путаются в названиях сторон, лучей, углов.

Видео:Первый признак равенства треугольников. 7 класс.Скачать

Доказательство подобия треугольников

Чуть позже появляется ещё одна важная тема «Подобие треугольников». Само определение «подобие» в геометрии означает схожесть формы при различии размеров. Для примера можно взять два квадрата, первый со стороной 4 см, а второй 10 см. Эти виды четырёхугольников будут похожи и, одновременно, иметь отличие, поскольку второй будет больше, причём каждая сторона увеличена в одинаковое количество раз.

В рассмотрении темы подобия также приводятся 3 признака:

• Первый — о двух соответственно равных углах двух рассматриваемых треугольных фигур.
• Второй — об угле и образующих его сторонах ∆ MNK , которые равны соответственным элементам ∆ SDH .
• Третий — указывает на пропорциональность всех соответственных сторон двух нужных фигур.

Как же доказать, что треугольники подобны? Достаточно воспользоваться одним из выше перечисленных признаков и грамотно описать весь процесс доказательства задания. Тема подобия ∆ MNK и ∆ SDH проще воспринимается школьниками исходя из того, что к моменту её изучения ученики уже свободно пользуются обозначениями элементов в геометрических построениях, не путаются в огромном количестве названий и умеют читать чертежи.

Завершая прохождение обширной темы треугольных геометрических фигур, учащиеся уже в совершенстве должны знать, как доказать равенство ∆ MNK = ∆ SDH по двум сторонам, установить равны два треугольника или нет. Учитывая, что многоугольник, имеющий ровно три угла — это одна из важнейших геометрических фигур, к усвоению материала следует подойти серьёзно, уделяя особое внимание даже мелким фактам теории.

🎦 Видео

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Задачи. Второй признак равенства треугольников. По рисункам. Доказать.Скачать

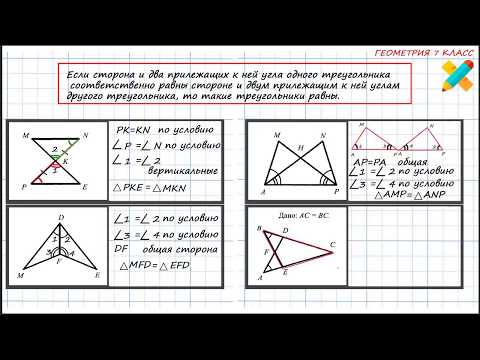
Геометрия.Задачи на второй и третий признаки равенства треугольниковСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Второй признак равенства треугольников. 7 класс.Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Шаталов за одну минуту доказывает теорему, на которую традиционно выделяется 45 минут урока!Скачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Параллельные прямые | Математика | TutorOnlineСкачать

7 класс, 19 урок, Второй признак равенства треугольниковСкачать

Почему углы при основании равны в равнобедренном треугольникеСкачать

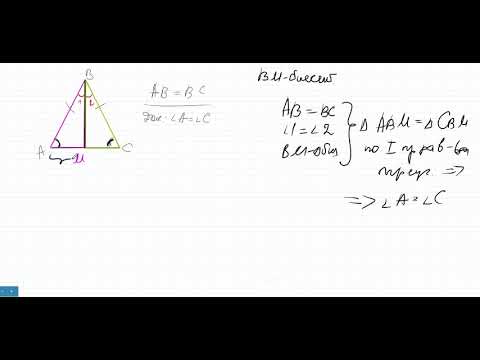
Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать