Доказать что треугольник pot sor

Определение

Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.

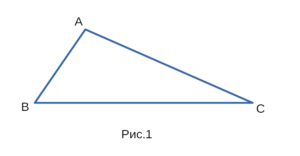
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.

Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.

Теорема

Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.

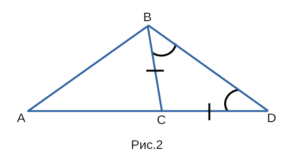
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:

Доказательство теоремы

1. Проведем отрезок CD равный отрезку CB.
2. △BCD — равнобедренный, значит ∠ CBD=∠CDB.
3. Рассмотрим △ABD: ∠ ABD >∠ CBD, следовательно ∠ ABD >∠ CDB, то AB

Видео:Признаки равенства треугольников. 7 класс.Скачать

Презентация по геометрии на тему «Второй признак равенства треугольников»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Второй признак равенства треугольников

Какая фигура называется треугольником? Какие треугольники называются равными? Как можно узнать, равны ли данные треугольники? Какие элементы достаточно рассмотреть для доказательства равенства треугольников?

Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников. Если сторона и два прилежащие к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Тест: 1. Для доказательства равенства треугольников АВС и MNK достаточно доказать, что: а) АС = MN; б) ∠C = ∠N; в) BC = MK. 2. Для доказательства равенства треугольников АСВ и EDF достаточно доказать, что: а) AC = FE; б) ∠C = ∠E; в) ∠A = ∠F. 3. Чтобы доказать равенство равносторонних треугольников АВС и MNK, достаточно доказать, что: а) ∠А = ∠М; б) АВ = МN; в) PABC = PMNK. 4. Чтобы доказать равенство двух равнобедренных треугольника TOS и DEF с основаниями TS и DF, достаточно доказать, что: а) ∠О = ∠Е; б) TS = DF и ∠Т = ∠D; в) TS = DF. 5. Выберите верное утверждение: а) ВС = КN; б) АВ = КN; в) ВС = NM. C A B K N M A B C F D E A B C M N K

Ответы: 1.в) 2.б) 3.б) 4.б) 5.а)

Задача № 1. Отрезки AB и CD пересекаются в точке O. Докажите равенство треугольников ACO и DOB если известно, что угол ACO равен углу DBO и BO=CO.

Решение: Рассмотрим ∆ ACO и ∆ DBO: BO=CO (по условию)

Отрезки AC и BD пересекаются в точке O. Докажите равенство треугольников BAO и DCO, если известно, что угол BAO равен углу DCO, AO = CO. Задача № 2.

Решение: Рассмотрим ∆ BAO и ∆ DCO. AO = CO (по условию)

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 976 человек из 78 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 308 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 677 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 551 690 материалов в базе

Другие материалы

• 30.11.2015
• 463
• 1

• 30.11.2015
• 465
• 1

• 30.11.2015
• 1297
• 13

• 30.11.2015
• 650
• 1

• 30.11.2015
• 316
• 0

• 30.11.2015
• 577
• 0

• 30.11.2015
• 598
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 30.11.2015 5122
• PPTX 149 кбайт
• 5 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Козулина Александра Вячеславовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 2 месяца
• Подписчики: 1
• Всего просмотров: 66161
• Всего материалов: 8

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

Новые курсы: управление детским садом, коучинг, немецкий язык и другие

Время чтения: 18 минут

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Онлайн-семинар о развитии управляющих функций мозга ребенка

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Минобрнауки подготовит государственный рейтинг университетов

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Первый признак равенства треугольников. 7 класс.Скачать

Теоремы Чевы и Менелая на ЕГЭ

Теоремы Чевы и Менелая на ЕГЭ

Подробная статья «Вокруг теорем Чевы и Менелая» опубликована на нашем сайте в разделе СТАТЬИ. Она адресована учителям математики и учащимся старших классов, мотивированным на хорошее знание математики. К ней можно вернуться, если появится желание подробнее разобраться в вопросе. В этой заметке мы приведем краткие сведения из упомянутой статьи и разберём решения задач из сборника для подготовки к ЕГЭ-2016.

Пусть дан треугольник ABC и на его сторонах AB, BC и AC отмечены точки C1, A1 и B1 соответственно (рис. 1).

а) Если отрезки AА1, BB1 и CС1 пересекаются в одной точке, то

. (1)

б) Если верно равенство (1), то отрезки AА1, BB1 и CС1 пересекаются в одной точке.

На рисунке 1 изображен случай, когда отрезки AА1, BB1 и CС1 пересекаются в одной точке внутри треугольника. Это так называемый случай внутренней точки. Теорема Чевы справедлива и в случае внешней точки, когда одна из точек А1, B1 или С1 принадлежит стороне треугольника, а две другие — продолжениям сторон треугольника. В этом случае точка пересечения отрезков AА1, BB1 и CС1 лежит вне треугольника (рис. 2).

Как запомнить равенство Чевы?

Обратим внимание на прием запоминания равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении обхода вершин треугольника ABC, начиная с точки A. От точки A идем к точке B, встречаем точку С1, записываем дробь . Далее от точки В идем к точке С, встречаем точку А1, записываем дробь . Наконец, от точки С идем к точке А, встречаем точку В1, записываем дробь . В случае внешней точки порядок записи дробей сохраняется, хотя две «точки деления» отрезка оказываются вне своих отрезков. В таких случаях говорят, что точка делит отрезок внешним образом.

Отметим, что любой отрезок, соединяющий вершину треугольника с любой точкой прямой, содержащей противоположную сторону треугольника, называют чевианой.

Рассмотрим несколько способов доказательства утверждения а) теоремы Чевы для случая внутренней точки. Чтобы доказать теорему Чевы, надо доказать утверждение а) любым из предложенных ниже способов, а также доказать утверждение б). Доказательство утверждения б) приведено после первого способа доказательства утверждения а). Доказательства теоремы Чевы для случая внешней точки проводятся аналогично.

Доказательство утверждения а) теоремы Чевы с помощью теоремы о пропорциональных отрезках

Пусть три чевианы AA1, BB1 и CC1 пересекаются в точке Z внутри треугольника ABC.

Идея доказательства заключается в том, чтобы отношения отрезков из равенства (1) заменить отношениями отрезков, лежащих на одной прямой.

Через точку В проведем прямую, параллельную чевиане СС1. Прямая АА1 пересекает построенную прямую в точке М, а прямая, проходящая через точку C и параллельная АА1, — в точке Т. Через точки А и С проведем прямые, параллельные чевиане ВВ1. Они пересекут прямую ВМ в точках N и R соответственно (рис. 3).

По теореме о пропорциональных отрезках имеем:

, и .

Тогда справедливы равенства

.

В параллелограммах ZСTM и ZСRВ отрезки TM, СZ и ВR равны как противоположные стороны параллелограмма. Следовательно, и верно равенство

.

Утверждение а) теоремы Чевы доказано.

При доказательстве утверждения б) используем следующее утверждение. Рис. 3

Лемма 1. Если точки С1 и С2 делят отрезок AB внутренним (или внешним) образом в одном и том же отношении, считая от одной и той же точки, то эти точки совпадают.

Докажем лемму для случая, когда точки С1 и С2 делят отрезок AB внутренним образом в одном и том же отношении: .

Доказательство. Из равенства следуют равенства и . Последнее из них выполняется лишь при условии, что С1B и С2B равны, т. е. при условии, что точки С1 и С2 совпадают.

Доказательство леммы для случая, когда точки С1 и С2 делят отрезок AB внешним образом проводится аналогично.

Доказательство утверждения б) теоремы Чевы

Пусть теперь верно равенство (1). Докажем, что отрезки AА1, BB1 и CС1 пересекаются в одной точке.

Пусть чевианы АА1 и ВВ1 пересекаются в точке Z, проведем через эту точку отрезок CС2 (С2 лежит на отрезке AB). Тогда на основании утверждения а) получаем верное равенство

. (2)

Из сравнения равенств (1) и (2) заключаем, что , т. е. точки С1 и С2 делят отрезок AB в одном и том же отношении, считая от одной и той же точки. Из леммы 1 следует, что точки С1 и С2 совпадают. Это означает, что отрезки AА1, BB1 и CС1 пересекаются в одной точке, что и требовалось доказать.

Можно доказать, что процедура записи равенства (1) не зависит, от того, от какой точки и в каком направлении совершается обход вершин треугольника.

Задание 1. Найдите длину отрезка АN на рисунке 4, на котором указаны длины других отрезков.

Задание 2. Чевианы AM, BN, CK пересекаются в одной точке внутри треугольника ABC. Найдите отношение , если , . Рис. 4

Ответ. .

Доказательство утверждения а) с помощью подобия треугольников

Приведем доказательство теоремы Чевы из статьи [1]. Идея доказательства заключается в том, чтобы заменить отношения отрезков из равенства (1) отношениями отрезков, лежащих на параллельных прямых.

Пусть прямые AA1, BB1, CC1 пересекаются в точке O внутри треугольника АВС (рис. 5). Через вершину С треугольника АВС проведем прямую, параллельную AB, и ее точки пересечения с прямыми AA1, BB1 обозначим соответственно A2, B2.

Из подобия двух пар треугольников CB2B1 и ABB1, BAA1 и CA2A1, Рис. 5

, . (3)

Из подобия треугольников BС1O и B2CO, AС1O и A2CO имеем равенства , из которых следует, что

. (4)

Перемножив равенства (3) и (4), получим равенство (1).

Утверждение а) теоремы Чевы доказано.

Рассмотрим доказательства утверждения а) теоремы Чевы с помощью площадей для внутренней точки. Оно изложено в книге [2] и опирается на утверждения, которые мы сформулируем в виде заданий 3 и 4.

Задание 3. Отношение площадей двух треугольников с общей вершиной и основаниями, лежащими на одной прямой, равно отношению длин этих оснований. Докажите это утверждение.

Задание 4. Докажите, что если , то и . Рис. 6

Доказательство утверждения а) с помощью площадей

Пусть отрезки AА1, BB1 и CС1 пересекаются в точке Z (рис. 6), тогда

, . (5)

Из равенств (5) и второго утверждения задания 4 следует, что или . Аналогично получим, что и . Перемножив три последние равенства, получим:

,

т. е. верно равенство (1), что и требовалось доказать.

Утверждение а) теоремы Чевы доказано.

Задание 15. Пусть чевианы пересекаются в одной точке внутри треугольника и разбивают его на 6 треугольников, площади которых равны S1, S2, S3, S4, S5, S6 (рис. 7). Докажите, что . Рис. 7

Задание 6. Найдите площадь S треугольника CNZ (площади других треугольников указаны на рисунке 8).

Задание 7. Найдите площадь S треугольника CNO, если площадь треугольника АNO равна 10 и , (рис. 9).

Задание 8. Найдите площадь S треугольника CNO, если площадь треугольника АBC равна 88 и , (рис. 9).

Решение. Так как , то обозначим, . Так как , то обозначим , . Из теоремы Чевы следует, что , и тогда . Если , то (рис. 10). У нас три неизвестные величины (x, y и S), поэтому для нахождения S составим три уравнения.

Так как , то = 88. Так как , то , откуда . Так как , то .

Итак, , откуда . Рис. 10

Задание 9. В треугольнике ABC точки K и L принадлежат соответственно сторонам AB и BC. , . P — точка пересечения отрезков AL и CK. Площадь треугольника PBC равна 1. Найдите площадь треугольника ABC.

Теорема Менелая

Пусть дан треугольник ABC и на его сторонах AC и CВ отмечены точки B1 и A1 соответственно, а на продолжении стороны AB отмечена точка C1 (рис. 11).

а) Если точки А1, B1 и С1 лежат на одной прямой, то

. (6)

б) Если верно равенство (7), то точки А1, B1 и С1 лежат на одной прямой. Рис. 11

Как запомнить равенство Менелая?

Прием запоминания равенства (6) тот же, что и для равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении обхода вершин треугольника ABC — от вершины к вершине, проходя через точки деления (внутренние или внешние).

Задание 10. Докажите, что при записи равенства (6) от любой вершины треугольника в любом направлении получается один и тот же результат.

Чтобы доказать теорему Менелая, надо доказать утверждение а) любым из предложенных ниже способов, а также доказать утверждение б). Доказательство утверждения б) приведено после первого способа доказательства утверждения а).

Доказательство утверждения а) с помощью теоремы о пропорциональных отрезках

I способ. а) Идея доказательства заключается в замене отношений длин отрезков в равенстве (6) отношениями длин отрезков, лежащих на одной прямой.

Пусть точки А1, B1 и С1 лежат на одной прямой. Через точку C проведем прямую l, параллельную прямой А1B1, она пересекает прямую АB в точке M (рис. 12).

Рис. 12

По теореме о пропорциональных отрезках имеем: и .

Тогда верны равенства .

Утверждение а) теоремы Менелая доказано.

Доказательство утверждения б) теоремы Менелая

Пусть теперь верно равенство (6), докажем, что точки А1, B1 и С1 лежат на одной прямой. Пусть прямые АB и А1B1 пересекаются в точке С2 (рис. 13).

Так как точки А1 B1 и С2 лежат на одной прямой, то по утверждению а) теоремы Менелая

. (7)

Из сравнения равенств (6) и (7) имеем , откуда следует, что верны равенства

, , .

Последнее равенство верно лишь при условии , т. е. если точки С1 и С2 совпадают.

Утверждение б) теоремы Менелая доказано. Рис. 13

Доказательство утверждения а) с помощью подобия треугольников

Идея доказательства заключается в том, чтобы заменить отношения длин отрезков из равенства (6) отношениями длин отрезков, лежащих на параллельных прямых.

Пусть точки А1, B1 и С1 лежат на одной прямой. Из точек A, B и C проведем перпендикуляры АА0, BB0 и СС0 к этой прямой (рис. 14).

Рис. 14

Из подобия трех пар треугольников AA0B1 и CC0B1, CC0A1 и BB0A1, C1B0B и C1A0A (по двум углам) имеем верные равенства

, , ,

перемножив их, получим:

.

Утверждение а) теоремы Менелая доказано.

Доказательство утверждения а) с помощью площадей

Идея доказательства заключается в замене отношения длин отрезков из равенства (7) отношениями площадей треугольников.

Пусть точки А1, B1 и С1 лежат на одной прямой. Соединим точки C и C1. Обозначим площади треугольников S1, S2, S3, S4, S5 (рис. 15).

Тогда справедливы равенства

, , . (8)

Перемножив равенства (8), получим:

.

Утверждение а) теоремы Менелая доказано.

Рис. 15

Подобно тому, как теорема Чевы остается справедливой и в том случае, если точка пересечения чевиан находится вне треугольника, теорема Менелая остается справедливой и в том случае, если секущая пересекает только продолжения сторон треугольника. В этом случае можно говорить о пересечении сторон треугольника во внешних точках.

Доказательство утверждения а) для случая внешних точек

Пусть секущая пересекает стороны треугольника ABC во внешних точках, т. е. пересекает продолжения сторон AB, BC и AC в точках C1, A1 и B1 соответственно и эти точки лежат на одной прямой (рис. 16).

По теореме о пропорциональных отрезках имеем:

и .

Тогда верны равенства

.

Утверждение а) теоремы Менелая доказано. Рис. 16

Заметим, что приведенное доказательство совпадает с доказательством теоремы Менелая для случая, когда секущая пересекает две стороны треугольника во внутренних точках и одну во внешней.

Доказательство утверждения б) теоремы Менелая для случая внешних точек аналогично доказательству, приведенному выше.

Задание 11. В треугольнике АВС точки А1, В1 лежат соответственно на сторонах ВС и AС. P — точка пересечения отрезков АА1 и ВВ1. , . Найдите отношение .

Решение. Обозначим , , , (рис. 17). По теореме Менелая для треугольника BCВ1 и секущей PA1 запишем верное равенство:

,

откуда следует, что

. Рис. 17

Ответ. .

Задание 12 (МГУ, заочные подготовительные курсы). В треугольнике АВС, площадь которого равна 6, на стороне АВ взята точка К, делящая эту сторону в отношении , а на стороне АС — точка L, делящая АС в отношении . Точка P пересечения прямых СК и ВL удалена от прямой АВ на расстояние 1,5. Найдите длину стороны АВ.

Решение. Из точек Р и С опустим перпендикуляры PR и СМ на прямую АВ. Обозначим , , , (рис. 18). По теореме Менелая для треугольника AKC и секущей PL запишем верное равенство: , откуда получим, что , . Рис. 18

Из подобия треугольников КMC и КRP (по двум углам) получим, что , откуда следует, что .

Теперь, зная длину высоты, проведенной к стороне AB треугольника ABС, и площадь этого треугольника, вычислим длину стороны: .

Задание 13. Три окружности с центрами А, В, С, радиусы которых относятся как , касаются друг друга внешним образом в точках X, Y, Z как показано на рисунке 19. Отрезки AX и BY пересекаются в точке O. В каком отношении, считая от точки B, отрезок CZ делит отрезок BY?

Решение. Обозначим , , (рис. 19). Так как , то по утверждению б) теоремы Чевы отрезки АX, BY и СZ пересекаются в одной точке — точке O. Тогда отрезок CZ делит отрезок BY в отношении . Найдем это отношение. Рис. 19

По теореме Менелая для треугольника BCY и секущей OX имеем: , откуда следует, что .

Ответ. .

Задание 14 (ЕГЭ-2016).

Точки В1 и С1 лежат на сторонах соответственно АС и АВ треугольника ABC, причём АВ1:B1С =
= АС1:С1B. Прямые ВВ1 и СС1 пересекаются в точке О.

а) Докажите, что прямая АО делит пополам сторону ВС.

б) Найдите отношение площади четырёхугольника AB1OC1 к площади треугольника ABC, если известно, что АВ1:B1С = 1:4. [8]

Решение. а) Пусть прямая AO пересекает сторону BC в точке A1 (рис. 20). По теореме Чевы имеем:

. (9)

Так как АВ1:B1С = АС1:С1B, то из равенства (9) следует, что , то есть CA1 = А1B, что и требовалось доказать. Рис. 20

б) Пусть площадь треугольника AB1O равна S. Так как АВ1:B1С = 1:4, то площадь треугольника CB1O равна 4S, а площадь треугольника AOC равна 5S. Тогда площадь треугольника AOB тоже равна 5S, так как треугольники AOB и AOC имеют общее основание AO, а их вершины B и C равноудалены от прямой AO. Причём площадь треугольника AOC1 равна S, так как АС1:С1B = 1:4. Тогда площадь треугольника ABB1 равна 6S. Так как АВ1:B1С = 1:4, то площадь треугольника CB1O равна 24S, а площадь треугольника ABC равна 30S. Теперь найдём отношение площади четырёхугольника AB1OC1 (2S) к площади треугольника ABC (30S), оно равно 1:15.

Задание 15 (ЕГЭ-2016).

Точки В1 и С1 лежат на сторонах соответственно АС и АВ треугольника ABC, причём АВ1:B1С =
= АС1:С1B. Прямые ВВ1 и СС1 пересекаются в точке О.

а) Докажите, что прямая АО делит пополам сторону ВС.

б) Найдите отношение площади четырёхугольника AB1OC1 к площади треугольника ABC, если известно, что АВ1:B1С = 1:3. [8]

Задание 16 (ЕГЭ-2016). На отрезке BD взята точка С. Биссектриса BL равнобедренного треугольника ABC с основанием ВС является боковой стороной равнобедренного треугольника BLD с основанием BD.

а) Докажите, что треугольник DCL равнобедренный.

б) Известно, что cosABC = . В каком отношении прямая DL делит сторону АВ? [8]

Решение. а) Пусть углы при основании BC равнобедренного треугольника ABC (рис. 21) равны , так как BL биссектриса ABC, то LBC = . Он равен углу LDB при основании BD равнобедренного треугольника BLD. Тогда внешний угол LCB треугольника DCL равен , а внутренний угол LDC, не смежный с ним, равен . Из свойства внешнего угла треугольника следует, что другой внутренний угол треугольника DCL равен – = , то есть треугольник DCL равнобедренный (DC = CL), что и требовалось доказать. Рис. 21

б) Пусть AK — медиана, проведённая к основанию BC равнобедренного треугольника ABC, она является высотой, поэтому BK:BA = cosABC = . Обозначим BK = x, тогда BC = 2x, BA = BС = 6x. Биссектриса BL делит сторону BС в отношении CL:LA = BC:BA = 1:3. Тогда CL = CD = = 1,5x.

По теореме Менелая , откуда, учитывая, что CL = CD, имеем: = .

Задание 17 (ЕГЭ-2016). На отрезке BD взята точка С. Биссектриса BL равнобедренного треугольника ABC с основанием ВС является боковой стороной равнобедренного треугольника BLD с основанием BD.

а) Докажите, что треугольник DCL равнобедренный.

б) Известно, что cosABC = . В каком отношении прямая DL делит сторону АВ? [8]

1. , Смирнов точки и линии треугольника. М.: Математика, 2006, № 17.

2. Мякишев геометрии треугольника. (Серия «Библиотека «Математическое просвещение»»). М.: МЦНМО, 2002. — 32 с.

3. Геометрия. Дополнительные главы к учебнику 8 класса: Учебное пособие для учащихся школ и классов с углубленным изучением / , , и др. — М.: Вита-Пресс, 2005. — 208 с.

4. Теоремы Чевы и Менелая. М.: Квант, 1990, № 3, С. 56–59.

5. Шарыгин Чевы и Менелая. М.: Квант, 1976, № 11, С. 22–30.

6. Вавилов и средние линии треугольника. М.: Математика, 2006, № 1.

7. Ефремов Дм. Новая геометрия треугольника. Одесса, 1902. — 334 с.

8. Математика. 50 вариантов типовых тестовых заданий / , , и др.; под ред. . – М.: Издательство «Экзамен», 2016. — 247 с.

🔥 Видео

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Первый признак равенства треугольников | Теорема + доказательствоСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Признаки равенства треугольников. Доказать равенство по рисунку. Найти пары.Скачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Третий признак равенства треугольников | Теорема + доказательствоСкачать

ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

Доказать,что треугольник равнобедренный. #ShortsСкачать

Задачи. Второй признак равенства треугольников. По рисункам. Доказать.Скачать

Третий признак равенства треугольников (доказательство) - геометрия 7 классСкачать

Две задачи по геометрии за 7 класс на тему: "Треугольники"Скачать

Второй признак равенства треугольников. 7 класс.Скачать

Задачи на доказательство равенства треугольников. Первый признак. Простые.Скачать

Задачи на доказательство по геометрии. Первый признак равенства треугольников.Скачать