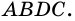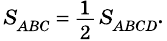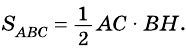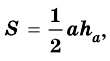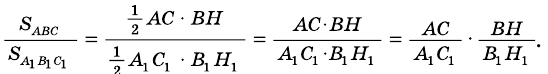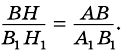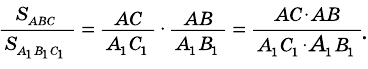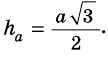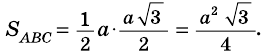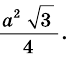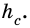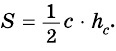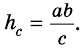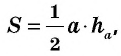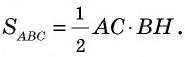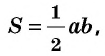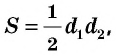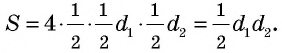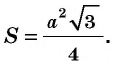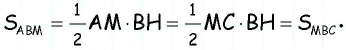Площадь треугольника:
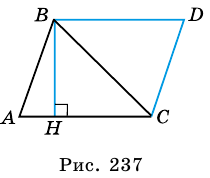
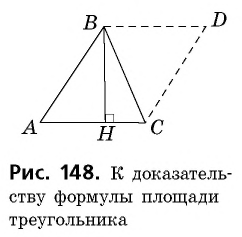
Теорема (о площади треугольника). Площадь треугольника равна половине произведения его стороны на высоту, к ней проведенную.
Доказательство:
Пусть
1) Проведем через вершину 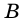
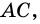
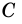
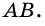
2) 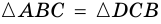
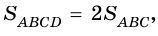
3) Так как 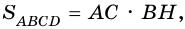
В общем виде формулу площади 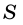
где 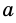
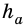
Следствие 1. Площадь прямоугольного треугольника равна половине произведения катетов.
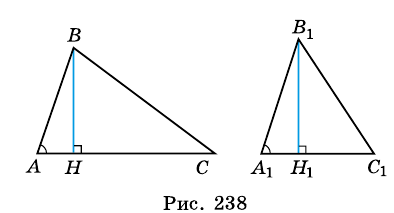
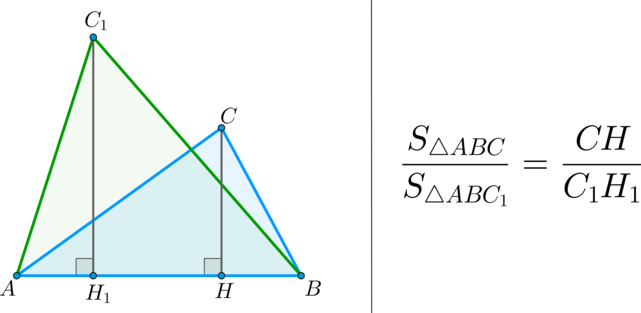
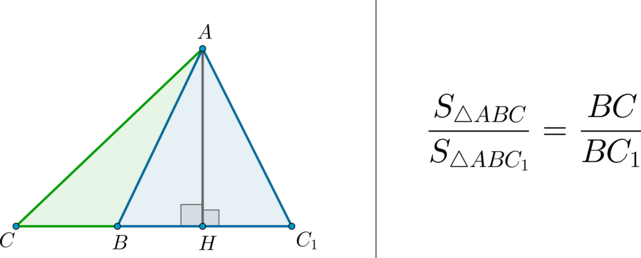
Следствие 2. Если сторона одного треугольника равна стороне другого треугольника, то площади таких треугольников относятся как их высоты, проведенные к этим сторонам.
Следствие 3. Если высота одного треугольника равна высоте другого треугольника, то площади этих треугольников относятся как стороны, к которым проведены эти высоты.
Пример:
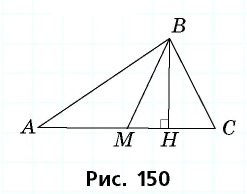
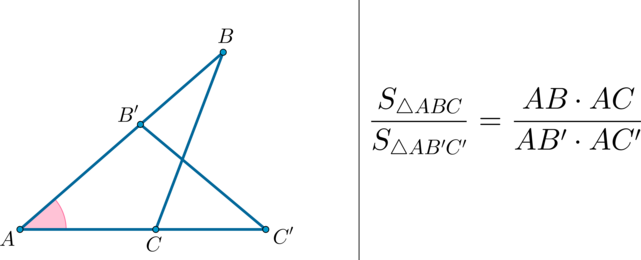
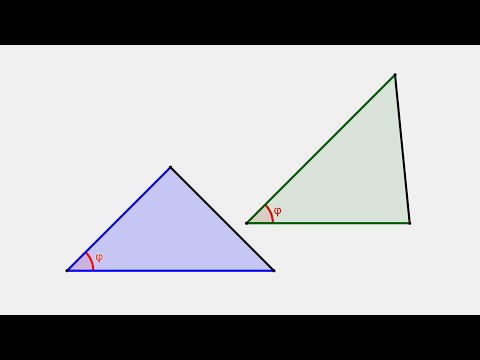
Докажите, что если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, образующих этот угол.
Доказательство:
Рассмотрим 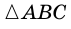
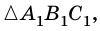
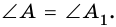
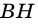
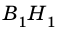
2) 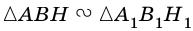
3) Имеем:
Пример:
Найдите площадь равностороннего треугольника, сторона которого равна
Решение:
Пусть 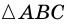
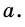
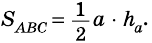
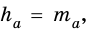
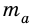
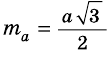
Следовательно,
Ответ.
Пример:
Стороны треугольника равны 8 см, 15 см и ^ 17 см. Найдите высоту треугольника, проведенную к его наибольшей стороне.
Решение:
Так как 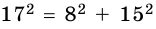
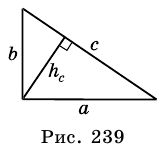
Пусть на рис. 239 изображен прямоугольный треугольник, у которого 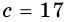
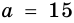
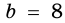
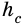
Площадь этого треугольника можно найти
по формулам: 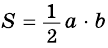
Тогда 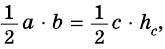
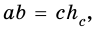
Таким образом, имеем: 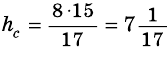
Ответ. 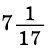
- Теорема (формула площади треугольника)
- Как найти площадь треугольника
- Основные понятия
- Формула площади треугольника
- Общая формула
- 1. Площадь треугольника через основание и высоту
- 2. Площадь треугольника через две стороны и угол между ними
- 3. Площадь треугольника через описанную окружность и стороны
- 4. Площадь треугольника через вписанную окружность и стороны
- 5. Площадь треугольника по стороне и двум прилежащим углам
- 6. Формула Герона для вычисления площади треугольника
- Для прямоугольного треугольника
- Площадь треугольника с углом 90° по двум сторонам
- Площадь треугольника по гипотенузе и острому углу
- Площадь прямоугольного треугольника по катету и прилежащему углу
- Площадь треугольника через гипотенузу и радиус вписанной окружности
- Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
- Площадь прямоугольного треугольника по формуле Герона
- Для равнобедренного треугольника
- Вычисление площади через основание и высоту
- Поиск площади через боковые стороны и угол между ними
- Площадь равностороннего треугольника через радиус описанной окружности
- Площадь равностороннего треугольника через радиус вписанной окружности
- Площадь равностороннего треугольника через сторону
- Площадь равностороннего треугольника через высоту
- Таблица формул нахождения площади треугольника
- Основные свойства площадей треугольников
- 💥 Видео
Видео:Теорема о площади треугольника | Геометрия 7-9 класс #95 | ИнфоурокСкачать

Теорема (формула площади треугольника)
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:
где 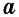
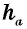
Пусть 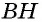
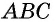
Проведем через вершины 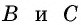
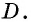
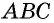
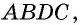
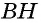
По формуле площади параллелограмма 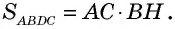
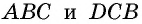
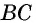
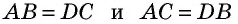
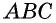
Следствие 1
Площадь прямоугольного треугольника равна половине произведения его катетов:
где 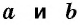
Действительно, в прямоугольном треугольнике высота, проведенная к катету, совпадает с другим катетом.
Следствие 2
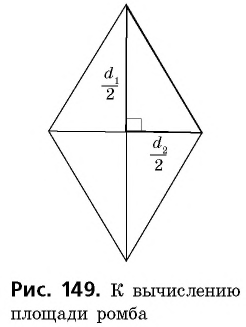
Площадь ромба равна половине произведения его диагоналей:
где 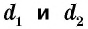
Действительно, диагонали делят ромб на четыре равных прямоугольных треугольника с катетами 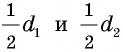
Следствие 3
Площадь равностороннего треугольника со стороной 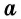
Обоснуйте это следствие самостоятельно.
Опорная задача
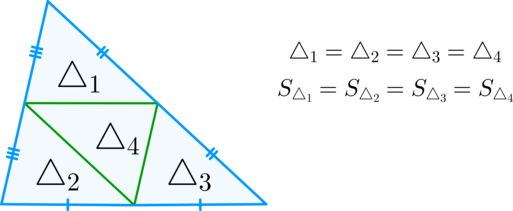
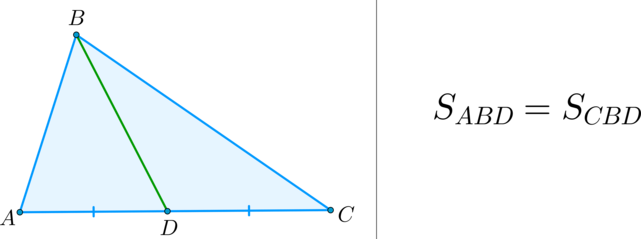
Медиана делит треугольник на два равновеликих треугольника. Докажите.
Решение:
Пусть 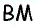
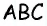
Проведем высоту 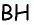
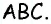
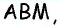
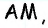
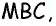
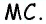
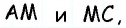
Эта задача имеет интересные обобщения: если высоты двух треугольников равны, то отношение площадей этих треугольников равно отношению их оснований; если основания двух треугольников равны, то отношение площадей этих треугольников равно отношению их высот.
Докажите эти утверждения самостоятельно.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Соотношения между сторонами и углами произвольного треугольника
- Окружность и круг
- Описанные и вписанные окружности
- Плоские и пространственные фигуры
- Взаимное расположения прямых на плоскости
- Треугольник
- Решение треугольников
- Треугольники и окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Видео:100. Теорема о площади треугольникаСкачать

Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Видео:Площадь по теореме Герона #математика #площадь #треугольник #герона #егэ #огэ #найтиплощадь #теоремаСкачать

Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Видео:Геометрия 9 класс : Теорема о площади треугольникаСкачать

Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
Видео:Площади треугольников с равным углом.Скачать

Основные свойства площадей треугольников
Факт 1.
(bullet) Средние линии треугольника разбивают его на 4 равных треугольника.
Соответственно, площади этих треугольников равны.
Факт 2.
(bullet) Медиана треугольника делит его на два треугольника, равных по площади (равновеликих).
Факт 3.
(bullet) Все 3 медианы треугольника делят его на 6 равновеликих треугольников.
Факт 4.
(bullet) Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.
Факт 5.
(bullet) Площади треугольников, имеющих одинаковое основание, относятся как высоты, проведенные к этим основаниям.
Факт 6.
(bullet) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.
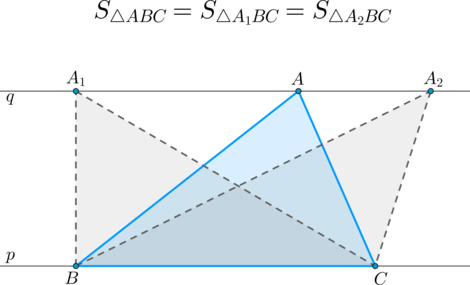
Факт 7.
(bullet) Если прямые (p) и (q) параллельны, то
Факт 8.
(bullet) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
(bullet) Отношение периметров подобных треугольников равно коэффициенту подобия.
💥 Видео
Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

11 класс, 47 урок, Формулы площади треугольникаСкачать

Теорема о площади треугольника.Скачать

8 класс, 14 урок, Площадь треугольникаСкачать

Теорема о площади треугольника. 9 классСкачать

9 класс. Геометрия. Площадь треугольника. Формулы для нахождения площади треугольника. Урок #3Скачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

ПЛОЩАДЬ ТРЕУГОЛЬНИКА формула 9 класс геометрия АтанасянСкачать

Секретные формулы площади треугольникаСкачать

Отношение площадей треугольников с равным угломСкачать
Геометрия 8. Урок 14 - Площадь треугольников. Формулы и задачи.Скачать