Для доказательства равенства треугольников авс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

тест по теме: «признаки равенства треугольников»

1. Для доказательства равенства треугольников АВС и NКМ достаточно доказать, что…

1) С = К;

2) С = М;

3) В = М.

2. Для доказательства равенства треугольников АPK и DCE достаточно доказать, что…

3. Из равенства треугольников АВК и MNF следует, что…

1) В = М;

2) В = N;

3) В = F.

4. Чтобы доказать равенство двух равнобедренных треугольников, недостаточно доказать равенство…

1) углов при основаниях;

2) оснований и углов при основаниях;

3) оснований и углов при вершине.

1) если сумма двух сторон и периметр одного треугольника соответственно равны сумме двух сторон и периметру другого треугольника, то такие треугольники равны;

2) если сумма двух сторон и угол между ними одного треугольника соответственно равны сумме двух сторон и углу между ними другого треугольника, то такие треугольники равны;

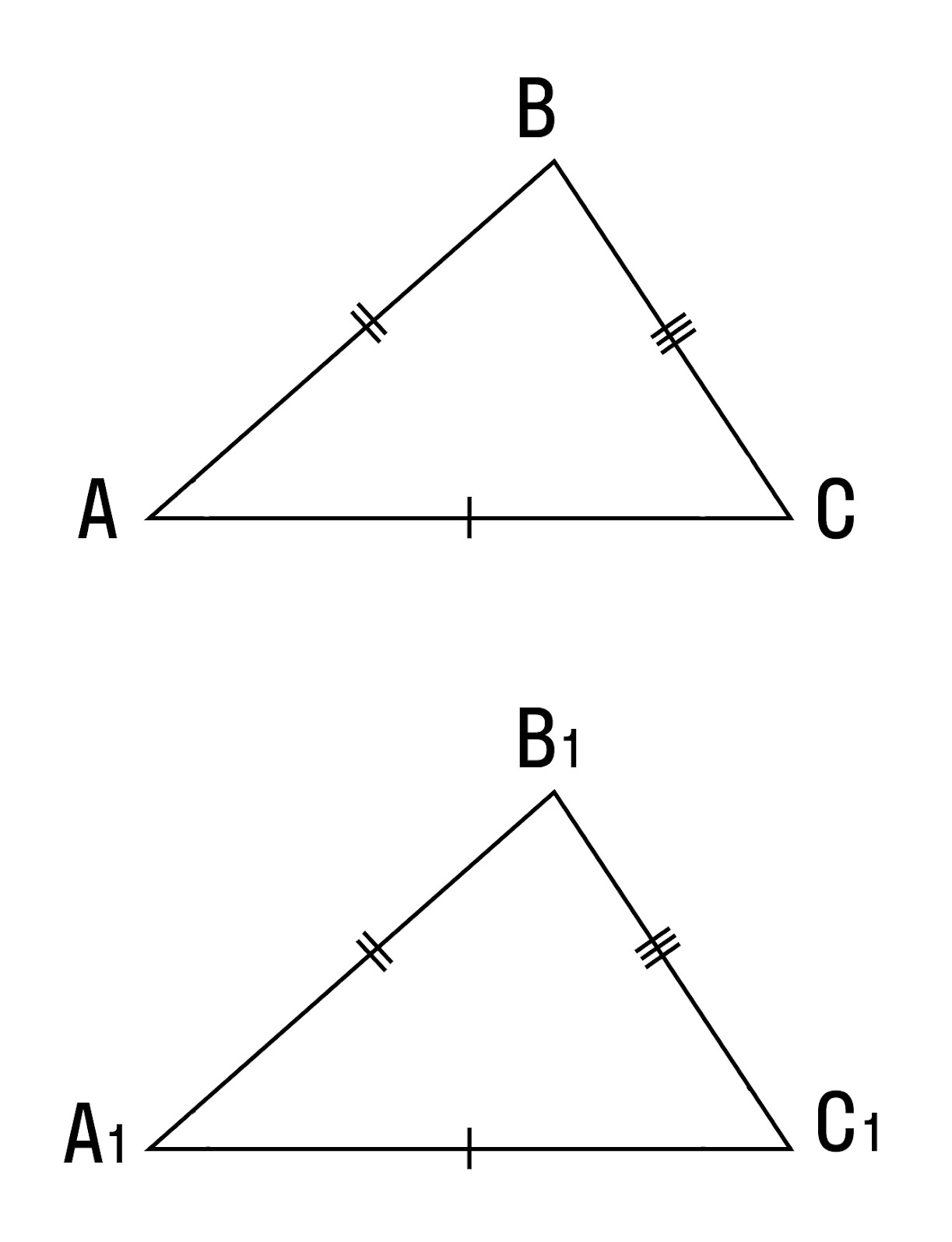
3) если две стороны и периметр одного треугольника соответственно равны двум сторонам и периметру другого треугольника, то такие треугольники равны.

1) АВ = А₁В₁, ВС = В₁С₁, А = А₁;

2) АС = А₁С₁, ВС = В₁С₁, С = С₁;

3) А = А₁, В = В₁, С = С₁.

7. В треугольниках АВС и MKN АВ = MK, ВС = NK, В = K.

В треугольниках проведены медианы (см. рис.).

8. Для данного четырехугольника неверно, что…

3) А = С.

9. Для данного четырехугольника верно, что…

1. ∆ МКР = ∆ М₁К₁Р₁, М = М₁, К₁Р₁ = 5 см.

2. ∆ АВС = ∆ MFK, В = М.

Тогда разность АС – FK равна…

3. Отрезки KP и EF пересекаются в точке М так, что KM = MP и EM = MF. PF = 12 см.

4. Медиана АМ треугольника АВС перпендикулярна стороне ВС.

ВАС = 40°.

Тогда ВАМ = …

5. В четырехугольнике АВСD 1 = 2, 3 = 4. ВD = 5 см.

Периметр четырехугольника равен 32 см. Тогда периметр треугольника АВD равен…

6. Точка О делит пополам диагональ…

тест по теме: «признаки равенства треугольников»

1. Для доказательства равенства треугольников АВС и КМР достаточно доказать, что…

2. Для доказательства равенства треугольников АВС и РEК достаточно доказать, что…

1) С = Е;

2) С = К;

3) С = Р.

3. Из равенства треугольников АРК и MFN следует, что…

3) A = M.

4. Чтобы доказать равенство двух равнобедренных треугольников, достаточно доказать равенство…

2) боковых сторон;

3) оснований и боковых сторон.

5. Какое высказывание неверное?

1) Если периметры равносторонних треугольников равны, то равны и треугольники.

2) Если периметры равнобедренных треугольников равны, то равны и треугольники.

3) Периметры равных равнобедренных треугольников равны.

1) АС = А₁С₁, В = В₁, С = С₁;

2) АВ = А₁В₁, АС = А₁С₁, С = С₁;

3) А = А₁, В = В₁, С = С₁.

7. В треугольниках АВС и MNP MP = AC, M = A, P = C.

В треугольниках проведены биссектрисы (см. рис.).

8. Для данного четырехугольника неверно, что…

3) В = D.

9. Для данного четырехугольника верно, что…

3) А = С.

1. ∆ АВС = ∆ А₁В₁С₁, ВС = В₁С₁, A = 35°.

Тогда A₁ = …

2. ∆ АВС = ∆ MFK, А = М.

Тогда отношение равно…

3. Отрезки AD и BC пересекаются в точке О так, что АО = OD и СО = ОВ.

CDO = 34°. Тогда ВАО = …

4. Биссектриса AD треугольника АВС перпендикулярна стороне ВС. ВС = 7,2 см.

5. В четырехугольнике MNPQ 1 = 2, 3 = 4. NQ = 9 см.

Периметр четырехугольника равен 28 см. Тогда периметр треугольника MNQ равен…

Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Признаки равенства треугольников

О чем эта статья:

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Видео:Признаки равенства треугольников. 7 класс.Скачать

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

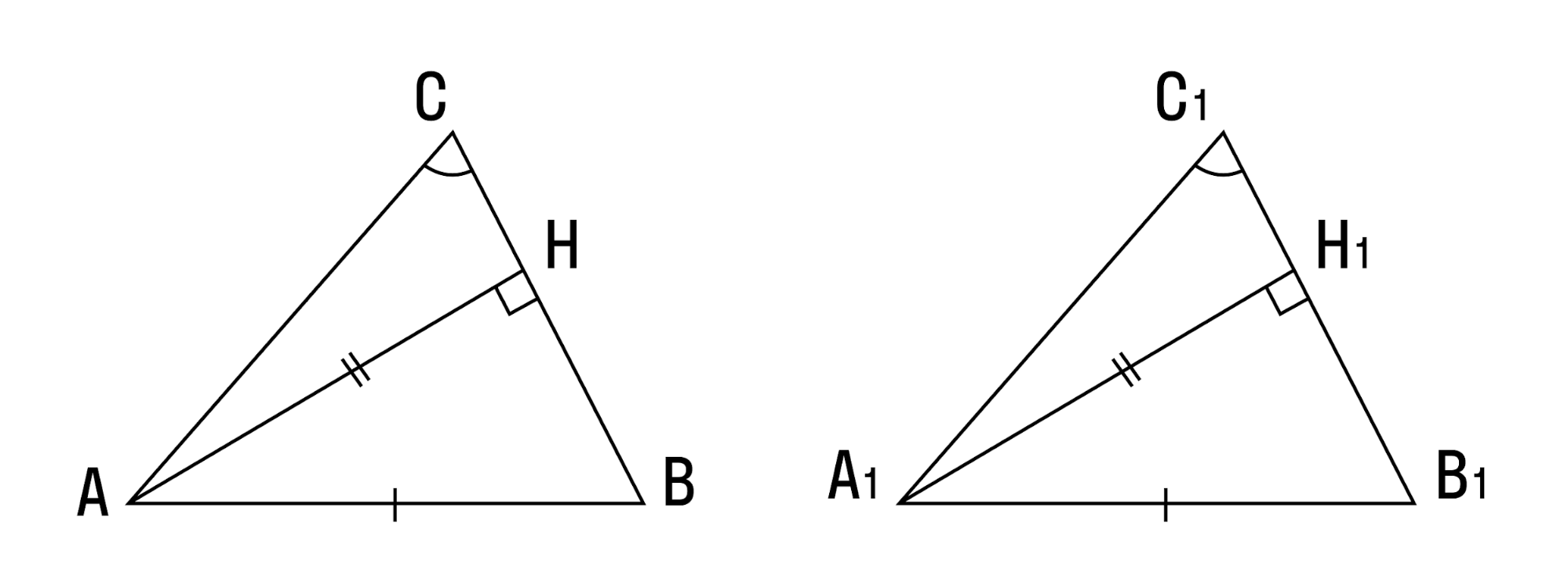
1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
   
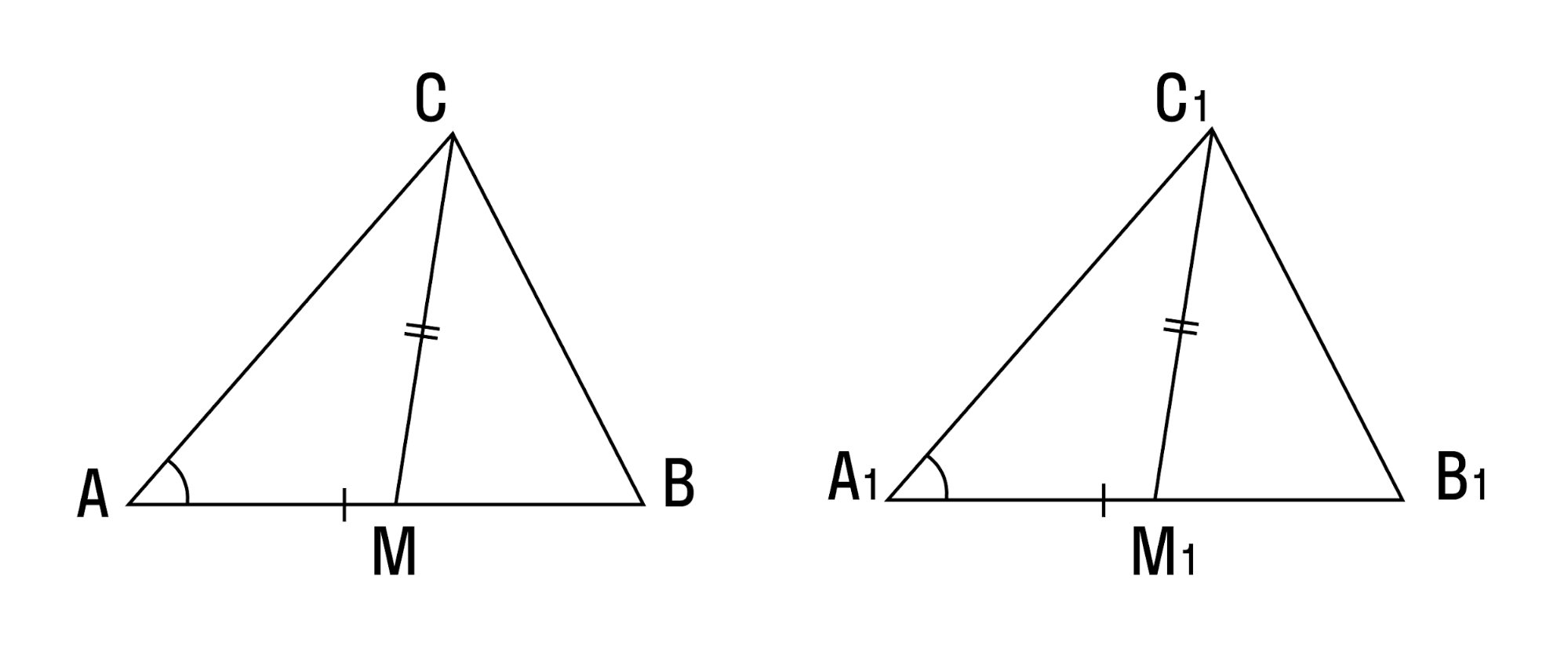
2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
   
3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
   
4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
   
5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
   

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Видео:Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать

Треугольники. Признаки равенства треугольников

Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .

Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.

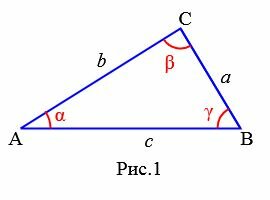Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.

Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.

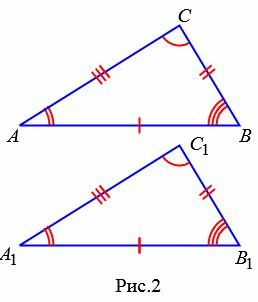
Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A₁B₁C₁. Треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.

Вышеизложенное можно сформулировать так:

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A₁B₁C₁ обозначается так:

Видео:Третий признак равенства треугольников | Теорема + доказательствоСкачать

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

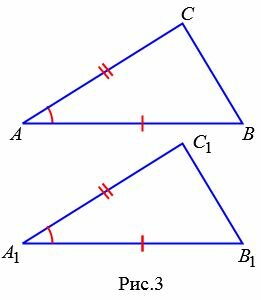Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и ∠A=∠A₁. Докажем, что .

Видео:ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

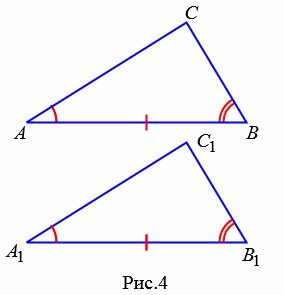Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁. Докажем, что .

Видео:Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

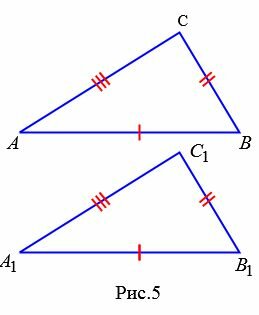Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

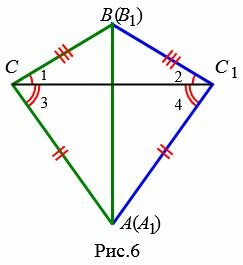Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

.

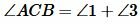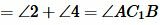Имеем AC=A₁C₁, BC=B₁C₁ ∠ACB=∠A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

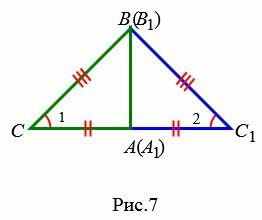Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда ∠1=∠2. Имеем: AC=A₁C₁, BC=B₁C₁, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.

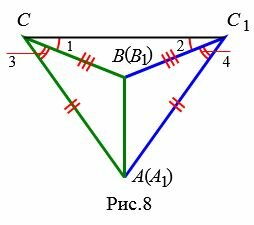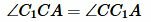
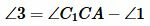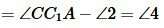Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и и, следовательно:

.

Имеем AC=A₁C₁, BC=B₁C₁ 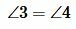и по первому признаку равенства треугольников . Теорема доказана.

Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

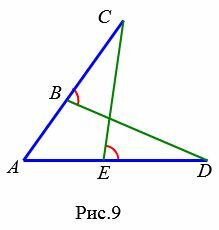Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства .

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

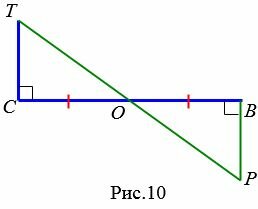Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .

💡 Видео

Второй признак равенства треугольников. 7 класс.Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Первый признак равенства треугольников. 7 класс.Скачать

Третий признак равенства треугольников (доказательство) - геометрия 7 классСкачать

Задание №1 "доказать равенство" по теме "Первый признак равенства треугольников". Геометрия 7 классСкачать

Первый признак равенства треугольников | Теорема + доказательствоСкачать

Геометрия. 7 класс. Теоремы. Т7. Второй признак равенства треугольников.Скачать

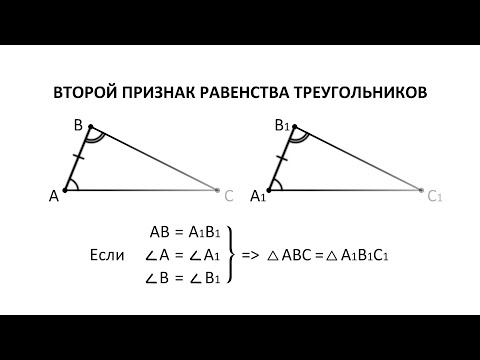
Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать

Первый признак равенства треугольников. Доказательство. Задачи по рисункам.Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Задачи на доказательство равенства треугольников. Первый признак. Простые.Скачать