план-конспект урока по алгебре (6 класс) на тему
Лабораторная работа – это такой метод обучения, при котором учащиеся под руководством учителя и по заранее намеченному плану проделывают опыты или выполняют определенные практические задания и в процессе их воспринимают и осмысливают новый учебный материал по определенным темам, применяют изученное на практике и закрепляют изученный материал
Важное условие совершенствования преподавания математики — усиление ее практической направленности.
Существенную роль в повышении эффективности обучения школьников играет сформированность у них практических умений и навыков геометрического характера (конструктивно-географических и измерительных), которые необходимы как для изучения математики, так и для повседневной деятельности.
Проведение лабораторных работ с учащимися вносит разнообразие в уроки математики; повышает активность и самостоятельность учащихся на уроке; способствуют повышению качества знаний по математике; делает абстрактные теоретические положения понятными, доступными, наглядными. Постепенное введение ФГОС в образовании учащимся дает возможность самим прийти к поставленной цели.
Лабораторная работа по теме «Длина окружности.Площадь круга.Шар» проводится в 6 классе классе. Урок проходит в группе. Работа состоит из 4 частей:
1). Предварительная подготовка к уроку. На этом этапе учащиеся готовят дома информацию о земном шаре (масса, диаметр, радиус, длина экватора и главного меридиана).
2). В теоретической части описывается ход выполнения и указываются формулы для вычисления длины окружности и площади круга;
3) В практической части составляют таблицу и вносят данные;
4) Итоги вычисления и вывод.
На момент проведения урока у учащихся сформировано понятия длины окружности, площади круга.
Для успешной работы на уроке подготовлены слайды, где отразились следующие этапы: тема урока, цель урока, основные принципы при выполнении работы, ход работы, результаты выполнения работы для сравнения вычислений учащихся, вывод урока, итог урока.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| Урок математики в 6 классе по теме Длина окружности.Площадь круга. Шар | 15.7 КБ |
| Презентация к уроку «Длина окружности Площадь круга.Шар» | 410 КБ |
Видео:Длина окружности. Математика 6 класс.Скачать

Предварительный просмотр:
Лабораторная работа (1,5 урока)
Тема: Длина окружности. Площадь круга. Шар.
1) длины окружности;
- площадь круга;
- длины экватора, меридианы и радиуса земного шара.
Развивающие задачи: развивать умение пользоваться ноутбуками, интерактивной доской, с интернетом.
- Воспитывающие задачи: воспитывать в каждом ученике чувства локтя;
- Работа в группе под девизом «Один за всех, все за одного»
Оборудование: Стаканы разного размера, нитка, линейка, пластинка, глобус, ноутбуки, планшеты,
I. Теоретическая часть .
Работа заключается в:
а) определении числа π, для чего необходимо предварительно измерить длины окружностей стаканов (С), диаметры окружностей стаканов (d) и найти числа π по формуле π = С/d;
б) определении длины окружности, площади круга пластинки по формулам С = 2πr, S = πr²;
в) вычислении длины экватора, длины меридиана и радиуса земного шара. Для этого с помощью нитки измерить длину экватора на глобусе, затем, используя масштаб, вычислить длину экватора, длину меридиана, радиус земного шара.
а) Определение числа π.
Длина окружности С (см)
Диаметр окружности d
б) Определение длины окружности, площади круга пластинки.
в) Вычисление длины экватора, длины меридиана и радиуса земного шара .
III. Познавательная работа в интернете:
Ответить на следующие вопросы:
- Найти информацию о земном шаре (масса, диаметр, радиус, длина экватора и главного меридиана)
- Сравнить ваши вычисления с данными в интернете
- Сделать вывод.
Предварительный просмотр:
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Подписи к слайдам:
Тема: Длина окружности. Площадь круга. Шар . Цель: Выполнение лабораторной работы Задачи: 1. Определение числа π. 2. Нахождение длины окружности, площади круга 3. Нахождение длины экватора, меридиана и радиуса Земного шара. Оборудование: Стакан, нитка, линейка, пластинка, глобус. Л А Б О Р А Т О Р Н А Я Р А Б О Т А
Взаимопомощь Взаимопонимание Сотрудничество Взаимоконтроль Взаимообучение Основные принципы выполнения работы
I . Теоретическая часть . Работа заключается в: а) определении числа π, для этого необходимо предварительно измерить длины окружности стакана (С), диаметр окружности стакана ( d ) и найти числа π по формуле π = С: d ; б) определении длины окружности, площади круга пластинки по формулам С = 2π r , S = π r ²; в) вычислении длины экватора, длины меридиана и радиуса земного шара. Для этого с помощью нитки измерить длину экватора на глобусе, затем, используя масштаб, вычислить длину экватора, длину меридиана, радиус земного шара. Ход работы
а) Определение числа π (пи) Вычисления: Приборы Длина окружности С (см) Диаметр окружности D ( c м) ЧИСЛО π Пластмассовый стакан Практическая часть
б) Определение длины окружности, площади круга пластинки. Вычисления: _________________________________________________________________________ в) Вычисление длины экватора, длины меридиана и радиуса земного шара. Вычисления: _________________________________________________________________________ Вывод: ______________________________________________________________________________ Практическая часть
№ Приборы Длина окружности С (см) Диаметр окружности D ( c м) Ч И С Л о π 1 Пластмассовый стакан 26 8,3 ≈ 3,13 1. Определение числа π Вычисление: С = 26 см, D = 8,3 см, тогда π = 26:8,3 = 3,13 Результаты выполнения
б) Определение длины окружности, площади круга пластинки. R = 12 см, C = 75,36 см, S= 452,16 см в) Вычисление длины экватора, длины меридиана и радиуса земного шара. C экватора = 80 · 50 000 000= 40000000000см= 40 000 км С меридиана = 40 · 50 000 000= 20 0000см=20 000 км R Земли = 40 000 км: 6,28 = 6369 км Фактическое значение: C экватора ≈ 40 000 км С меридиана ≈ 20 000 км R Земли ≈ 6 378 км (6356 км)
Убедились, что число π ≈ 3,14 Закрепили формулы для вычисления длины окружности, площади круга Сами определили длину экватора, меридиана и радиуса Земли Вывод
1 — я группа -5 2 — я группа -5 3 — я группа -5 4 — я группа -5 5 — я группа -5 Итог урока
Важную роль в математике играет число , равное отношению длины окружности к ее диаметру c : d . Это число π. Оно получило широкое распространение после работ Леонарда Эйлера – академика Российской академии наук в XVIII веке (1707-1783). Исторические сведения
Ученные вычисляли значение π с разной точностью. Так, великий греческий математик и механик Архимед ( III в.до н.э.) доказал, что Мне нравится
Видео:Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Лабораторная работа по математике на тему: «Вывод формулы длины окружности и площади круга»
Разделы: Математика
Цели урока
- Обучающие. Опытным путем получить зависимость между длиной окружности и её диаметром, вывести формулы длины окружности и площади круга.
- Развивающие. Способствовать дальнейшему развитию внимания, наблюдательности, самоконтроля учащихся.
- Воспитательные. Воспитывать аккуратность и дисциплинированность школьников, умение работать в тишине, помогать товарищам.
Учащиеся должны иметь с собой картон, лист цветной бумаги, ножницы, нитки, циркуль, цветной карандаш, простой карандаш, клей-карандаш, калькулятор, линейку, фломастер.
Ход урока
В первую очередь актуализируются опорные знания, необходимые для выполнения лабораторной работы. Учащимся предлагается ответить на следующие вопросы:
- Что называют отношением двух величин?
- Как округлить десятичную дробь до десятых? До сотых?
- Чему равна площадь прямоугольника?
- Что такое окружность? Радиус? Диаметр?
- Если фигуру площадью S разделить на части с площадями S1 и S2, будет ли выполняться равенство S=S1+S2
- Если фигуру площадью S разделить на части и из них составить другую фигуру, будет ли её площадь равна площади первоначальной фигуры?
Учащиеся выполняют практические задания по команде учителя и записывают свои наблюдения (учитель может все проделывать на доске, если класс не достаточно подготовлен к самостоятельной работе, или предложить ученикам работать в парах).
- На картонном листе начертить окружность с произвольным радиусом, отметить её центр, записать значение радиуса в миллиметрах(R) и значение диаметра в миллиметрах(D).
- Провести клеем-карандашом по окружности и, пока клей не высох, проложить нитку точно по контуру окружности и аккуратно отрезать её на стыке.
- Снять нитку с картона и очень точно измерить её длину в миллиметрах. Этот размер назовем длиной окружности(L). Записать значение L.
- Найти отношение
с помощью калькулятора, округлить получившуюся дробь до тысячных, до сотых, до десятых, до целых. Сделать соответственные записи.
Далее ученики называют свои результаты и замечают, что, хотя окружности были построены у всех разные, отношения длины к диаметру получились примерно одинаковые.
Отношение длины окружности к её диаметру – величина постоянная и не зависит от размеров окружности. Число, выражающее это отношение, принято называть греческой буквой 

В глубокой древности считалось, что окружность ровно в 3 раза длиннее диаметра. Эти сведения содержатся в клинописных табличках Древнего Междуречья. Итак, первым приближением числа 
Три первые цифры числа 
Нужно только постараться
И запомнить все как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
С.Бобров. “Волшебный двурог”
Вывод формулы длины окружности.
Итак, мы имеем следующее соотношение: 



Учащимся предлагается выполнить несколько упражнений:
- D=6см, найти L.
- R=3дм3мм, найти L.
- L=6см, найти R.
- L=8
мм, найти R.
Вывод формулы площади круга.
Учащиеся выполняют практические задания по команде учителя (учитель может проделывать все на доске).
- На листе цветной бумаги начертить окружность с произвольным радиусом и провести фломастером по её контуру.
- Разделить круг с помощью линейки и карандаша на несколько секторов, затем разрезать его. (см. рис.1) Заметим, что не следует делить круг на меньшее, чем 8 секторов.
- В одном из секторов следует провести радиус, делящий его на 2 равных сектора, которые назовём крайними (см. рис.2) и отложить.
- На картонном листе провести горизонтальную прямую и приклеить вдоль неё сектора, как показано на рис.3. (На рис.3,а – круг разделен на 8 секторов, на рис.3,б – на 16 секторов). Крайние сектора приклеить по краям. Заметно, что получившаяся фигура при увеличении количества секторов становится очень похожей на прямоугольник. Значит, и её площадь можно найти по формуле площади прямоугольника. Ширина нашего прямоугольника равна радиусу окружности(R), а длина прямоугольника равна половине длины окружности (
). Площадь прямоугольника равна произведению длины на ширину, т. е. S=
, а т.к. L=2
R, значит S=
или S=
R 2 .
.Так как прямоугольник был составлен из частей круга, то их площади равны. Значит, площадь круга равна: S=

Применение формул для решения задач.
- Сравнить площади кругов с радиусами 3дм и 300мм.
- Найти площадь круга, если D=6см.
- Найти площадь круга, если L=10
.
- Сравнить площадь круга с R=5см с площадью квадрата со стороной 5см.
Следует отметить, что этот этап нужно включать в ход урока, если использован двухчасовой урок. В этом случае можно провести небольшую проверочную работу, которую учащиеся выполнят прямо на своих картонных листах. Учитель оценит правильность решения задач и аккуратность выполнения практической части.
В противном случае оценивается только практическая часть.
Комментарий: Данный урок является нетрадиционным, что особенно нравится детям любого возраста. Практика показывает, что получение или вывод формул “своими силами” прочно запоминается ввиду своей наглядности, четко простроенной цепочки выводов. Для учащихся 5-6 классов формулы длины окружности и площади круга – одни из первых, которые надо прочно запомнить. Так пусть дети их выведут сами!
Видео:Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

Лабораторная работа по математике «Длина окружности и площадь круга»
Длина окружности с
Диаметр окружности d
Отношение длины окружности к диаметру
3. Найдите площадь квадрата АВС D
4. Сравните площадь треугольника MNO и площадь квадрата AMON
S MNO в . раза …. чем S AMON
5. А теперь сравните площадь квадрата MNRK и площадь квадрата АВС D
6. S АВС D вы уже знаете, найдите S MNRK
7. Площадь круга меньше S MNRK , но больше S АВС D . Значит, ……
8 . Сделаем предположение, что …….
S круга
3. Найдите площадь квадрата АВС D
4. Сравните площадь треугольника MNO и площадь квадрата AMON
S MNO в . раза …. чем S AMON
5. А теперь сравните площадь квадрата MNRK и площадь квадрата АВС D
6. S АВС D вы уже знаете, найдите S MNRK
7. Площадь круга меньше S MNRK , но больше S АВС D . Значит, ……
8 . Сделаем предположение, что …….
S круга
3. Найдите площадь квадрата АВС D
4. Сравните площадь треугольника MNO и площадь квадрата AMON
S MNO в . раза …. чем S AMON
5. А теперь сравните площадь квадрата MNRK и площадь квадрата АВС D
6. S АВС D вы уже знаете, найдите S MNRK
7. Площадь круга меньше S MNRK , но больше S АВС D . Значит, ……
8 . Сделаем предположение, что …….
S круга
3. Найдите площадь квадрата АВС D
4. Сравните площадь треугольника MNO и площадь квадрата AMON
S MNO в . раза …. чем S AMON
5. А теперь сравните площадь квадрата MNRK и площадь квадрата АВС D
6. S АВС D вы уже знаете, найдите S MNRK
7. Площадь круга меньше S MNRK , но больше S АВС D . Значит, ……
8 . Сделаем предположение, что …….
S круга
Тема урока: Длина окружности и площадь круга.
обучающие: 1) ввести формулы для нахождения длины окружности и площади круга;
2) сформировать и закрепить навыки применения формул для решения задач;
развивающие: 1) продолжить развитие у учащихся интереса к предмету;
2) продолжить развитие устной и письменной математической речи;
3) продолжить развитие памяти, внимания, мышления;
4) продолжить развитие исследовательских умений;
воспитательные: 1) продолжить воспитание у учащихся аккуратности, самоконтроля в выполнение
2) продолжить воспитание способности высказывать и доказывать свое мнение.
Оборудование: доска, предметы цилиндрической формы, линейка, нить, циркуль, плакаты с цитатами, портрет Архимеда, магнитофон, индивидуальные таблицы для лабораторной работы.
Учитель: Здравствуйте, ребята. Сегодня мы проведем необычный урок. Вы заметили, что на дверях нашего кабинета написано «МАТЕМАТИЧЕСКАЯ ЛАБОРАТОРИЯ» и слова древнего философа Платона «Пусть никто, не знакомый с математикой, не входит сюда».
Сейчас мы перенесемся в прошлое, в 3 век до н.э. Представим, что мы древнегреческие мудрецы и попробуем сделать математические открытия!
Актуализация опорных знаний.
Учитель: Прежде чем пробовать свои силы, нам необходимо повторить некоторые знания, которые нам необходимы для совершения великих открытий. Дома вы должны были повторить такие понятия как круг, окружность, радиус, диаметр, длина окружности и вспомнить, что называют отношением двух чисел.
По чертежу на доске ребята повторяют все вышеперечисленные понятия.
Изучение нового материала, путем выполнения лабораторной работы.
Учитель: Ребята, в моих руках диск. Могу ли я найти его радиус, его диаметр, длину окружности? Согласитесь, измерять длину окружности с помощью нити не совсем удобно. Сегодня мы должны сделать открытие: как найти длину окружности по-другому.
Запишем тему урока: «Длина окружности ……»
Девизом нашего урока будут слова Б. Шоу «Единственный путь, ведущий к знаниям – это деятельность».
Ребята, теперь работаем в паре и, используя необходимые инструменты (предметы, цилиндрической формы, линейку, нить), заполняем таблицу.
Для создания творческой атмосферы можно включить приятную спокойную мелодию.
Учитель: Что вы заметили, ребята?
(с : d 
Учитель: Ребята, я поздравляю вас, это наше первое открытие! Оказывается, что отношение длины окружности к ее диаметру есть величина постоянная и равна она 3,14159
Доказал это древний математик Архимед в 3 в. до н.э.
Это число имеет свое название – число «пи» (
И с тех пор многие ученые стали находить более точные значения этого числа. Совсем недавно 59-летний японец запомнил число 
Итак, с : d = 
Найдите, чему равна длина окружности.
с = d
А как найти длину окружности через радиус?
с = 2
Давайте найдем длину окружности нашего диска!
(Ученик у доски решает данную задачу).
Задание1: Построить три окружности различных радиусов, найти длину каждой окружности, взяв 
Задание2: Найти диаметр и радиус по длине окружности, взяв 
Учитель: Вернемся к нашему диску. Как математики, какую еще величину мы можем найти?
Интересно, чему равна площадь круга?
Попробуем сделать второе открытие. Допишем тему урока «…… и площадь круга».
Площадь каких фигур мы умеем находить? (прямоугольника и квадрата). Эти знания нам пригодятся.
Итак, как же найти площадь круга? Открытие это совсем не простое, надо очень постараться!
Продолжаем работать в парах. Внимание на доску. Внимательно рассмотрите рисунок и заполните таблицу.
3. Найдите площадь квадрата АВС D
4. Сравните площадь треугольника MNO и площадь квадрата AMON
S MNO в . раза …. чем S AMON
5. А теперь сравните площадь квадрата MNRK и площадь квадрата АВС D
6. S АВС D вы уже знаете, найдите S MNRK
7. Площадь круга меньше S MNRK , но больше S АВС D . Значит, ……
8 . Сделаем предположение, что …….
S круга
В старших классах мы докажем, что S круга = 
Задание 3: Ребята, найдите площадь диска (ученик у доски) и кругов, построенных в тетрадях.
Ребята, какие вы молодцы. Какие важные открытия вы сделали!
— Что вы открыли сегодня?
— Пригодятся ли ваши открытия человечеству?
— Что особенно понравилось на уроке?
Постановка домашнего задания.
Дома выучить формулы, которые вы открыли, написать мини – сочинение «Как я открыл формулу».
🌟 Видео
КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Лабораторная работа № 7 по физике для 7 классаСкачать

10 класс - Лабораторная работа № 1 - Изучение движения тела по окружностиСкачать

Масштаб. 6 класс.Скачать

Длина окружности. 9 класс.Скачать

Котика ударило током, 10 т. ВольтСкачать

Лабораторная работа "Изучение движения шарика по окружности"Скачать

Площадь круга. Практическая часть - решение задачи. 6 класс.Скачать
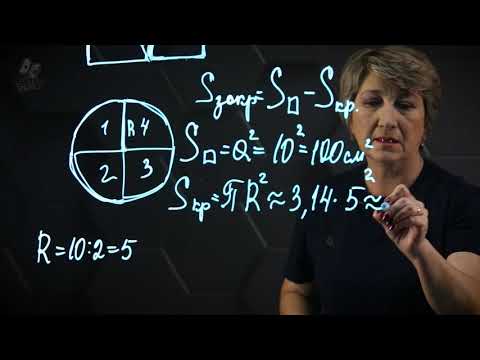
Лабораторный эксперимент №4 - Изучение движения тела по окружности (9 класс)Скачать

Лабораторная работа № 2 по физике для 7 класса А.В. ПерышкинСкачать

Центральная симметрия. 6 класс.Скачать

МЕРЗЛЯК-6. ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА. ПАРАГРАФ-25Скачать

Лабораторная работа №2 Измерение размеров малых телСкачать

Длина окружности. Практическая часть. 9 класс.Скачать

Длина окружности. Площадь круга, 6 классСкачать



 мм, найти R.
мм, найти R.

 ). Площадь прямоугольника равна произведению длины на ширину, т. е. S=
). Площадь прямоугольника равна произведению длины на ширину, т. е. S= , а т.к. L=2
, а т.к. L=2 R, значит S=
R, значит S=  или S=
или S= R 2 .
R 2 .
 .
.