Длина ленты трех окружностей (2 видео) | Курс школьной геометрии

Простая задача про круги, которая выглядит сложной

Но на деле она точно простая.

Разберём свежую задачу с канала MindYourDecisions. Это не про программирование, но развивает логическое мышление.

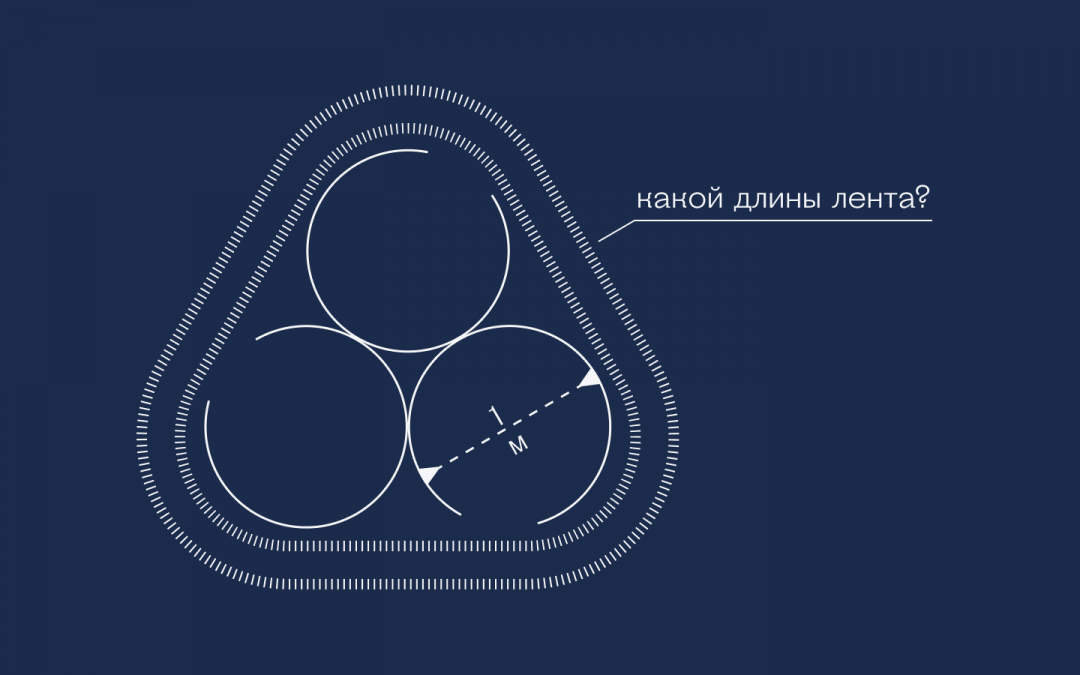
Дано: есть три одинаковых круга с диаметром в 1 метр. Круги соприкасаются друг с другом, а вокруг них натянута эластичная лента.

Что нужно: найти длину этой ленты.

Кажется, что это очень сложная задача, где нужно знать сложные формулы расчёта кривизны и точек натяжения, но на деле всё будет гораздо проще. Если знаете английский — посмотрите оригинальный ролик, там классная анимация:

Содержание

Строим внутренний треугольник
Строим проекцию
Вычисляем длину секций
Задача про круги: кажется сложной, но она очень простая!
Строим треугольник
Создаем проекцию
Находим длину секций
Love Soft
Инструменты пользователя
Инструменты сайта
Боковая панель
Навигация
Связь
Содержание
Длина окружности, площадь круга (задачи)
Задача 1
Задача 2
Задача 3
Что больше: периметр квадрата или длина окружности?
Почему крышки люков круглые
Задача (вступительные в колледж)
📺 Видео

Видео:Радиус и диаметрСкачать

Строим внутренний треугольник

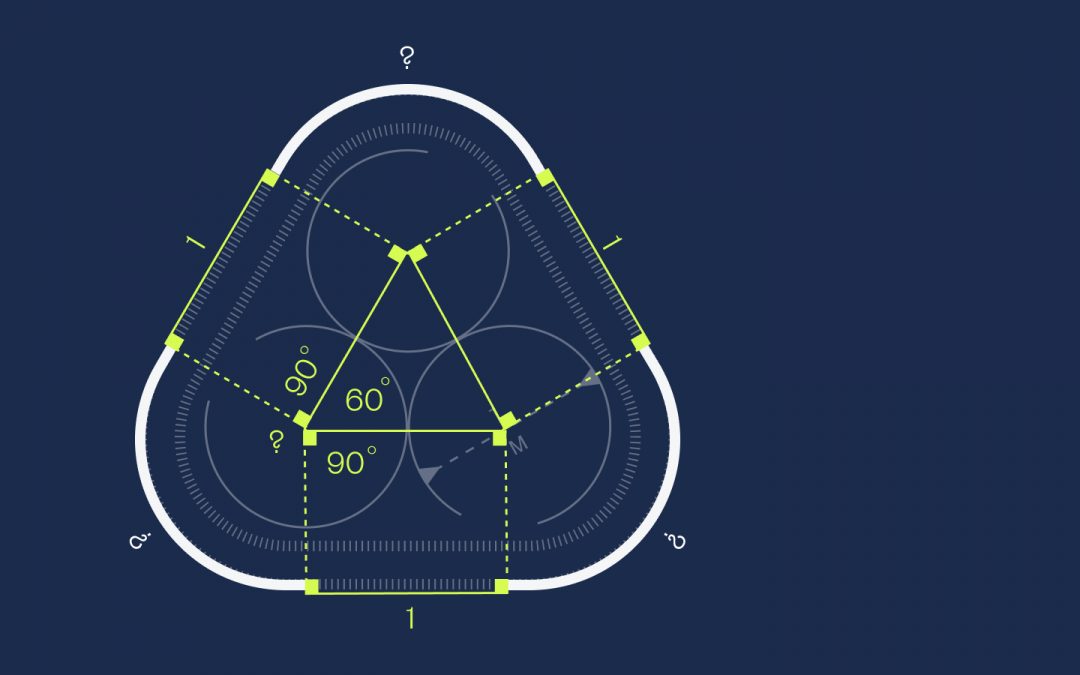
Первое, что мы сделаем, — соединим центры всех кругов в один треугольник:

В геометрии есть такое правило, что если круги касаются друг друга, то через их центры можно провести прямую линию, и точка касания кругов будет лежать на этой линии. Раз у нас диаметр равен 1, то радиус каждого круга равен 0,5. Обозначим это на рисунке:

Получается, что длина каждой стороны треугольника равна 0,5 + 0,5 = 1. Запомним это и идём дальше.

Видео:Длина окружности. Математика 6 класс.Скачать

Строим проекцию

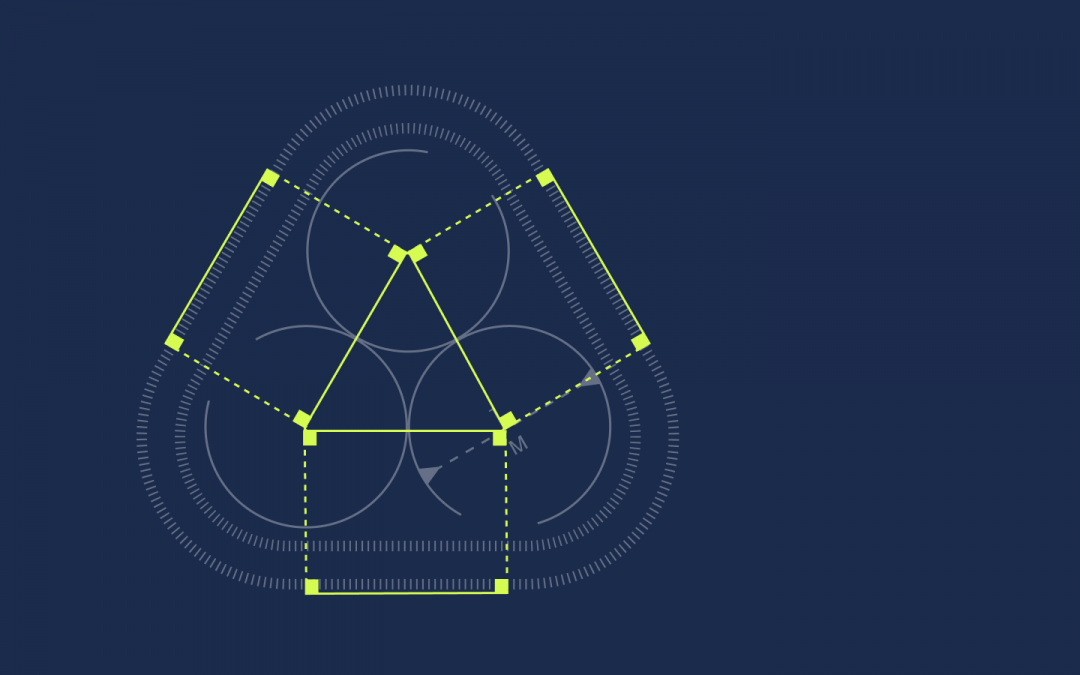
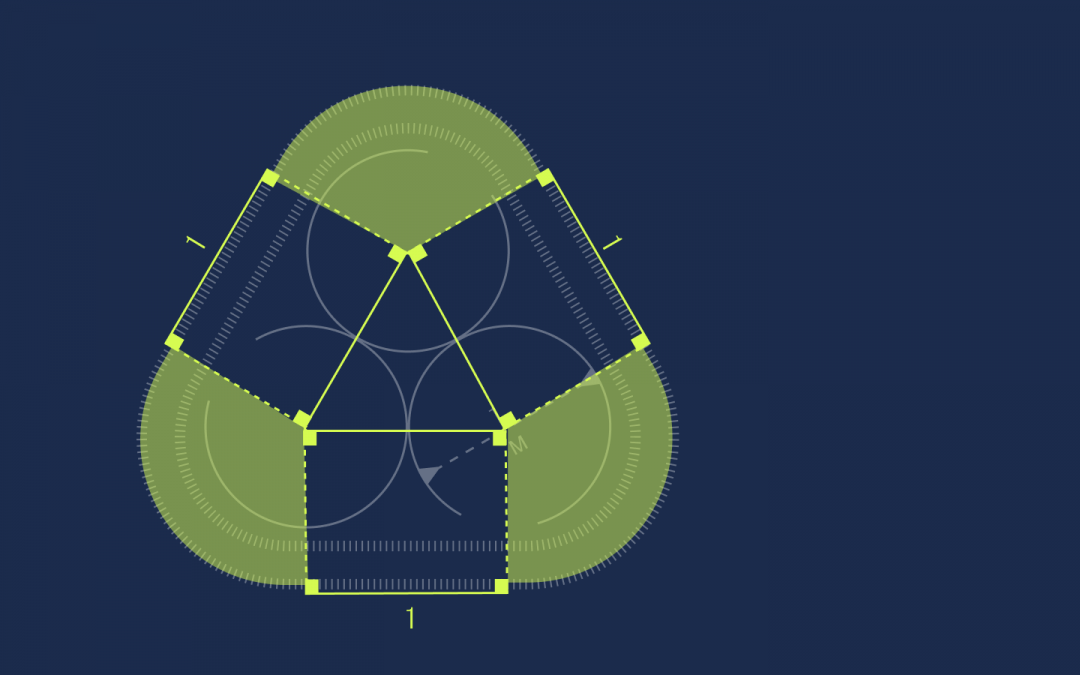
От каждой вершины треугольника проведём под прямым углом линии к ленте:

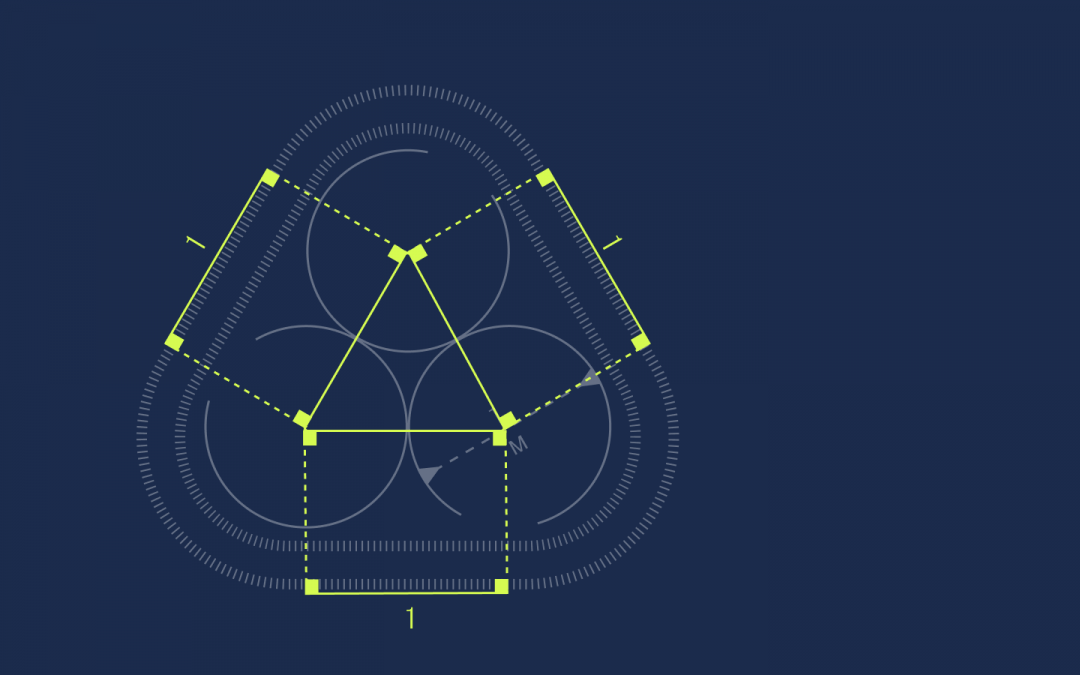
Получились прямоугольники. У прямоугольников противоположные стороны равны, поэтому раз стороны треугольника равны единице, то и эти отрезки на ленте тоже будут равны единице:

Осталось найти длину оставшихся секций:

Видео:Деление окружности на 3 частиСкачать

Вычисляем длину секций

Здесь нам поможет знание о том, что полный оборот внутри круга — это 360 градусов.

Так как во внутреннем треугольнике все стороны равны, то это равносторонний треугольник. А раз так, то углы в нём равны 60 градусов. Добавим сюда по два прямых угла по 90 градусов из прямоугольников:

Решаем уравнение: 90 + 60 + 90 + X = 360 → X = 120 градусов.

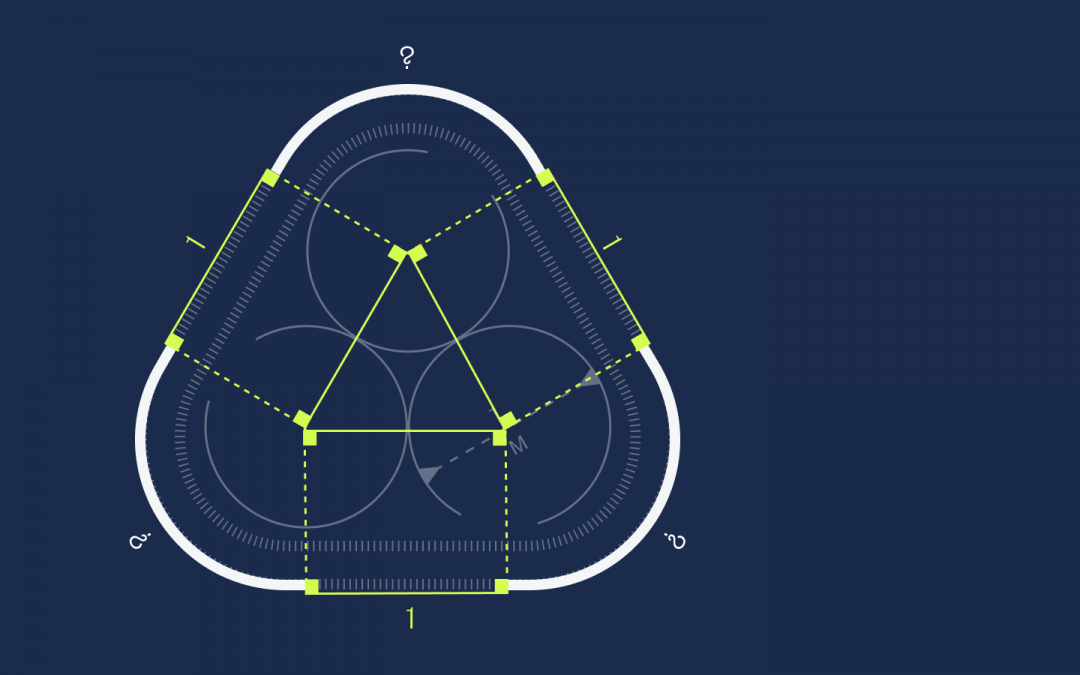
Но 120 градусов — это ровно треть круга, а у нас таких частей как раз три:

Это значит, что из них можно составить один целый круг. При этом мы знаем, что у этого круга радиус 0,5, а диаметр тогда равен единице. Этого достаточно, чтобы посчитать длину окружности: L = π × d → L = 3,14.

Складываем это число с длинами трёх отрезков и получаем полную длину: 3 + π

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Задача про круги: кажется сложной, но она очень простая!

Раздумывая над решением, не спешите сдаваться. Все гораздо легче, чем вам может показаться на первый взгляд. И пусть здесь нет программирования, зато есть возможность развивать логическое мышление.

Условие: даны три одинаковых соприкасающихся круга диаметром 1 м. Их опоясывает эластичная лента.

Задание: найдите длину ленты, натянутой вокруг кругов.

Для того чтобы найти ответ, вам не нужны сложные формулы, такие как расчет кривизны и т.п. На самом деле все гораздо проще.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Строим треугольник

Для начала соединим центры кругов таким образом, чтобы получился треугольник.

По законам геометрии, центры соприкасающихся кругов можно соединить прямой линией, причем точка касания будет находиться именно на ней. Так как диаметр равен 1 метру, радиусы всех кругов равны 0,5 метра. Укажем это на схеме:

Выходит, что стороны треугольника равны между собой и длина каждой из них составляет 0,5 + 0,5 = 1. Зафиксируем это и двигаемся дальше.

Видео:Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Создаем проекцию

Все вершины треугольника соединим с лентой линиями, проведенными под углом 90°.

Получились прямоугольники. Как известно, противоположные стороны этой фигуры равны, а раз длина каждой стороны треугольника равна 1, данные отрезки ленты также равны 1:

Теперь нужно найти длину трех оставшихся секций:

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Находим длину секций

В круге 360 градусов. Треугольник, который мы построили из центров кругов, равносторонний. Следовательно, каждый угол в нем равен 60°. У прямоугольников углы по 90°. Обозначим все это на схеме:

Находим неизвестный угол:

90 + 60 + 90 + X = 360

120° — это ровно одна третья часть круга, а мы имеем 3 таких части:

Получается, что все вместе они формируют один полный круг. Нам известно, что радиус данного круга равен 0,5, а диаметр – 1. Это позволяет вычислить длину окружности:

Прибавляем к этому числу длины 3-х отрезков и получаем длину всей ленты: 3 + π.

Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Love Soft

Инструменты пользователя

Инструменты сайта

Боковая панель

Содержание

Видео:+Как найти длину окружностиСкачать

Длина окружности, площадь круга (задачи)

Задача 1

У Белого Кролика были часы со стрелками длиной 3 см и 5 см. Найди длины окружностей, которые описывают своими концами стрелки, совершая полный круг. Вычисли площадь кольца, заключенного между этими двумя окружностями. Найди длину пути часовой стрелки, который она пройдет за 3 часа. Число пи округли до единиц.

Задача 2

Длина окружности ствола берёзы равна 50 см.
Каков его радиус? Какова площадь поперечного сечения этого ствола?

Задача 3

Выразить свой возраст в единицах пи.

Что больше: периметр квадрата или длина окружности?

Пусть точка E — середина стороны AD квадрата ABCD.

Пусть окружность проходит через точки E, B и C.

Что больше: периметр квадрата или длина окружности?

Проведем диаметр окружности, так чтобы он был перпендикулярен стороне квадрата, как на рисунке:

Радиус окружности примем равным 1 (поскольку он все равно сокращается при нахождении отношения двух периметров), тогда длина окружности равна 2 пи.

Периметр квадрата согласно обозначениям равен $8y$.

Находим y из системы

Отсюда $y = 4/5 = 0.8$ (от радиуса окружности)

Периметр квадрата = $8 cdot 0.8 = 6.4 > 2*pi$ (то есть больше длины окружности).

Тут еще нужно обоснование, почему центр окружности лежит на средней линии квадрата. Это следует из того, что центр окружности лежит на пересечении диагоналей вписанного прямоугольника

2-е решение. Нужно найти радиус описанной окружности вокруг равнобедренного треугольника EBC, боковая сторона которого равна половине корня из 5 (примем сторону квадрата за 1). Площадь этого треугольника равна половине площади квадрата, то есть 1/2.

Периметр квадрата 4. Длина окружности $5/4 cdot pi$

1A-е решение. Пусть радиус = 5. Тогда образуется треугольник со сторонами 3,4 и 5 (Любимый Треугольник Экзаменатора). (Это следует из решения 1). $$frac = frac = frac Периметр квадрата больше длины окружности

Почему крышки люков круглые

Квадратная крышка может упасть в люк и нанести травму работающим внизу людям или утонуть. Так произойдет, потому что диагональ квадрата больше, чем его сторона, — это соотношение корень квадратный из двух (1,414…). Когда квадратную крышку приподнимают почти вертикально, то, если крышка при этом даже немного поворачивается в направлении диагонали люка, она может соскользнуть и упасть внутрь люка. У круглой крышки, напротив, диаметр одинаков, какое бы направление вы ни выбрали. С учетом того, что диаметр верхней поверхности круглой крышки чуть больше, чем нижней, она вообще никогда не может соскользнуть внутрь люка, в каком бы положении ее ни держали.

Колодцы люков круглые, потому что круглые канализационные колодцы легче копать, чем квадратные.

Еще один возможный ответ: круглую крышку можно не носить, а катить на короткие расстояния, а для переноски квадратной крышки понадобятся два человека или тачка. Дополнительный, правда менее важный довод: круглую крышку не нужно вращать и разворачивать, чтобы совместить с отверстием люка, закрывая его.

Этот вопрос, наверное, один из самых известных среди тех, что задает Microsoft.

Верхняя поверхность крышки должна быть рельефной с высотой рельефа 2—6 мм.

Крышки канализационных люков обычно весят 50 кг и больше, чтобы они не могли быть сдвинуты с люка даже при сильном автомобильном движении.

У круглого люка отношение площади сечения лаза к длине окружности его корпуса больше, чем у квадратного или прямоугольного, что позволяет снизить себестоимость производства за счёт сокращения расхода материалов без ухудшения эксплуатационных показателей. (диаметр лаза люка в действующих стандартах близкий к 600 мм — при круглой форме длина окружности корпуса — 1,88 м, при квадратной — 2,4 м, площадь крышки круглой формы — 0,28 м², площадь крышки квадратной формы — 0,36 м². Т. о. перерасход материалов на производство люка при переходе от круглой к квадратной его форме люков составит 28 %).

Крышку можно выполнить в форме треугольника Рёло — благодаря постоянной ширине этой фигуры она не сможет провалиться в люк