Длина большей стороны треугольника

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

,

Фигура	Рисунок	Формулировка
Треугольник
Большая сторона треугольника		Против большей стороны треугольника лежит больший угол
Больший угол треугольника		Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника		Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника		Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника
		Углы треугольника
Внешний угол треугольника
Больший угол треугольника
Меньший угол треугольника
Теорема косинусов
Теорема синусов

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

,

Треугольник
Большая сторона треугольника
	Против большей стороны треугольника лежит больший угол
Больший угол треугольника
	Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника
	Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника
	Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника
	Углы треугольника
Внешний угол треугольника
Больший угол треугольника
Меньший угол треугольника
Теорема косинусов
Теорема синусов

Треугольник

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Большая сторона треугольника

Свойство большей стороны треугольника:

Против большей стороны треугольника лежит больший угол

Больший угол треугольника

Свойство большего угла треугольника:

Против большего угла треугольника лежит большая сторона

Меньшая сторона треугольника

Свойство меньшей стороны треугольника:

Против меньшей стороны треугольника лежит меньший угол

Меньший угол треугольника

Свойство меньшего угла треугольника:

Против меньшего угла треугольника лежит меньшая сторона

Длины сторон треугольника

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Углы треугольника

Свойство углов треугольника:

Сумма углов треугольника равна 180°

Внешний угол треугольника

Свойство внешнего угла треугольника:

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Больший угол треугольника

Свойство большего угла треугольника:

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Меньший угол треугольника

Свойство меньшего угла треугольника:

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

Теорема косинусов

Теорема синусов

Свойство меньшего угла треугольника:

,

Длина большей стороны треугольника равна 5, 6 дм, и она меньше большей стороны на 1, 9 дм?

Математика | 5 — 9 классы

Длина большей стороны треугольника равна 5, 6 дм, и она меньше большей стороны на 1, 9 дм.

Найдите периметр треугольника, если длина его третьей стороны равна среднему арифметическому двух сторон.

Большая сторона — 5.

меньшая сторона — 5.

третья сторона — (5.

Периметр треугольника равен 13см ?

Периметр треугольника равен 13см .

Две его сторонны равны между собой, а третья сторона 3 см.

Найди длину двух равных сторон треугольника.

Периметр равнобедренного треугольника равен 33дм?

Периметр равнобедренного треугольника равен 33дм.

, а равные стороны имеют длины по 12 дм.

Найдите длину третьей стороны.

Найди длину каждой из двух равных сторон треугольника если его периметр равен 50 дм а третья сторона 16 см?

Найди длину каждой из двух равных сторон треугольника если его периметр равен 50 дм а третья сторона 16 см.

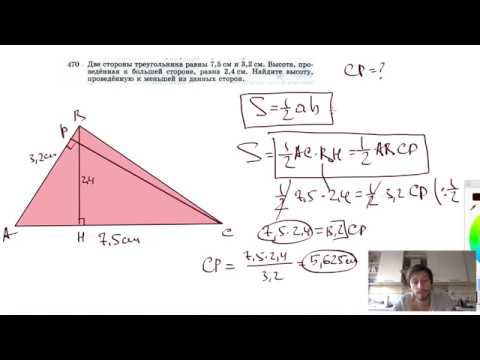
Найди длину каждой из двух равных сторон треугольника если его периметр равен 50 дм а третья сторона 16 дм?

Найди длину каждой из двух равных сторон треугольника если его периметр равен 50 дм а третья сторона 16 дм.

Длина одной стороны треугольника равна 4 3 / 5 дм?

Длина одной стороны треугольника равна 4 3 / 5 дм.

Длина другой стороны — на 1 2 / 5 дм меньше, длина третьей стороны — на 3 3 / 5 дм меньше суммы длин двух других сторон.

Вычислите периметр этого треугольника.

Периметр прямоугольника равен 1, 8 дм а длины двух его сторон равны по 0, 5 дм?

Периметр прямоугольника равен 1, 8 дм а длины двух его сторон равны по 0, 5 дм.

Найдите длину третьей стороны треугольника.

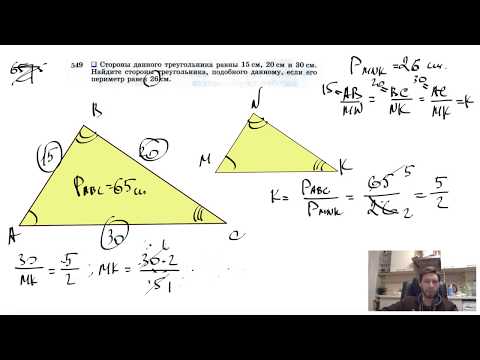
Длина одной стороны треугольника равны 56 дм , что 24 дм больше длины второй стороны и на 18 дм меньше третьей стороны?

Длина одной стороны треугольника равны 56 дм , что 24 дм больше длины второй стороны и на 18 дм меньше третьей стороны.

Вычислите периметр треугольника ?

Периметр треугольника — 3, 4 дм, длинна одной стороны — 1, 4 дм, длины двух других сторон равны?

Периметр треугольника — 3, 4 дм, длинна одной стороны — 1, 4 дм, длины двух других сторон равны.

Найдите длины равных сторон треугольника.

Периметр треугольника равен 1, 8 дм, а длины двух его сторон равны по 0, 5 дм?

Периметр треугольника равен 1, 8 дм, а длины двух его сторон равны по 0, 5 дм.

Найдите длину третьей стороны треугольника.

Две стороны треугольника имеют одинаковую длину, равную 60 дм?

Две стороны треугольника имеют одинаковую длину, равную 60 дм.

Периметр треугольника 1600см.

Найди длину третьей стороны.

Если вам необходимо получить ответ на вопрос Длина большей стороны треугольника равна 5, 6 дм, и она меньше большей стороны на 1, 9 дм?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Математика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α		sin β		sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 — 2 bc · cos α

b 2 = a 2 + c 2 — 2 ac · cos β

c 2 = a 2 + b 2 — 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 — a 2

m_b = 1 2 √ 2 a 2 +2 c 2 — b 2

m_c = 1 2 √ 2 a 2 +2 b 2 — c 2

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p — a ) b + c

l_b = 2√ acp ( p — b ) a + c

l_c = 2√ abp ( p — c ) a + b

где p = a + b + c 2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

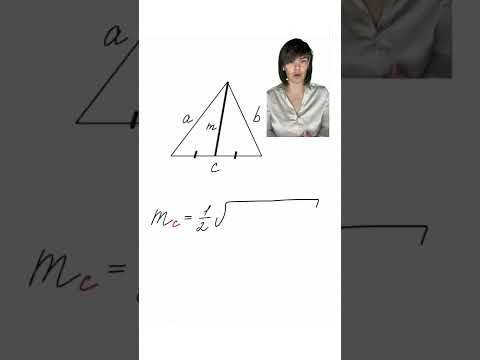
Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

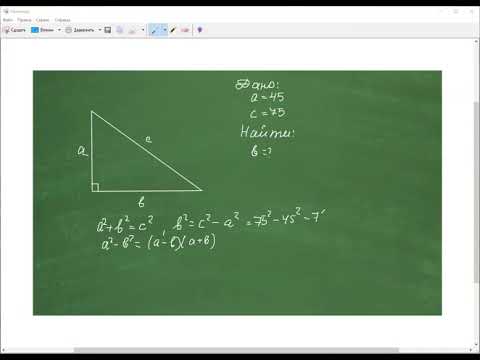
Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

S =	a · b · с
	4R

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.