Диаметр окружности основания цилиндра 20 образующая 28 (3 видео)

Цилиндр диаметр 20 образующая цилиндра равна 28

Содержание

Решите пожалуйста задачу с решением Диаметр окружности основания равен 20, Образующая =28.Плоскость пересекает основания цилиндра по хордам длины 12 и 16.Найдите tg угла между этой плоскостью и плоскостью основания цилиндра. Заранее спасибо)))))))
Цилиндр диаметр 20 образующая цилиндра равна 28
Как посчитать объем цилиндра
Онлайн калькулятор
Зная радиус r и высоту h
Формула
Пример
Зная диаметр d и высоту h
Формула
Пример
Зная площадь основания So и высоту h
Формула
Пример
Зная площадь боковой поверхности Sb и высоту h
Формула
Пример
Диаметр окружности основания цилиндра 20 образующая 28
Быстрая регистрация
Математика (проф. ур.) (Вариант 1)
🎬 Видео

Видео:№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать

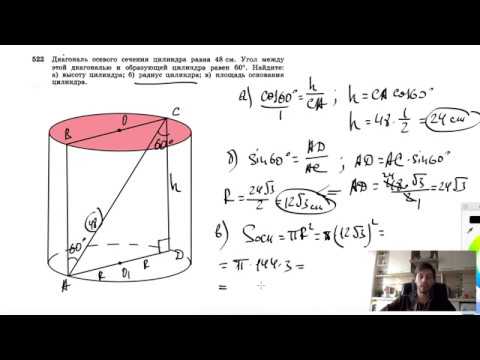
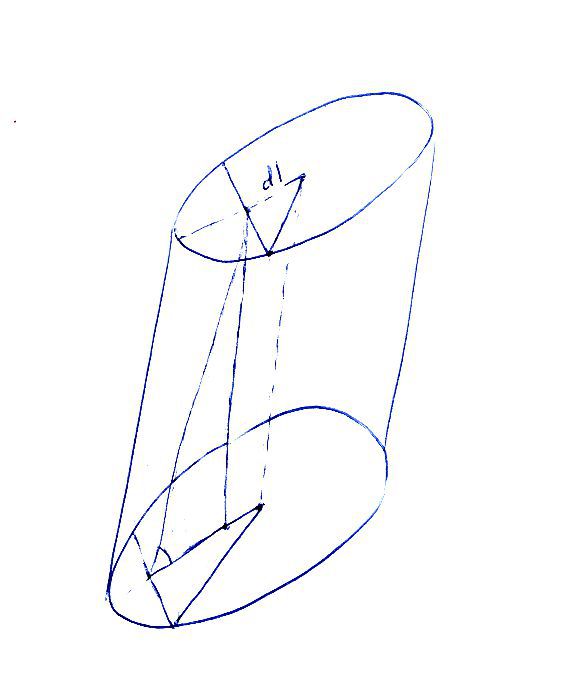
Решите пожалуйста задачу с решением Диаметр окружности основания равен 20, Образующая =28.Плоскость пересекает основания цилиндра по хордам длины 12 и 16.Найдите tg угла между этой плоскостью и плоскостью основания цилиндра. Заранее спасибо)))))))

На довольно корявом чертеже я нарисовала, как строится двугранный угол между плоскостью сечения и основанием. Ясно видно, что все, что надо найти — это расстояния от центров оснований до хорд. До хорды 2 расстояние d1 = корень(10^2 — 6^2) = 8; до хорды 16 расстояние d2 = 6.

Искомый тангенс двугранного угла равен образующей, деленной на РАЗНОСТЬ этих расстояний, то есть

4м 9дм = 4 × 10 + 9дм = 40дм + 9дм = 49дм

Так как 1м = 10дм, то выразим метр в дециметрах и прибавим 9дм

Найдите значение выражения:

а) 0,7542х + 0,2458х — 20,9 если х = 220
х-20.9=220-20.9=199.1
Ответ: 199.1
б) 66,6у — 44,4у + 8,11 если у = 10
22.2у+8.11=222+8.11=230.11
Ответ: 230.11

Видео:№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

Цилиндр диаметр 20 образующая цилиндра равна 28

В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 4, а боковое ребро SA равно 7. На рёбрах CD и SC отмечены точки N и K соответственно, причём DN : NC = SK : KC = 1 : 3. Плоскость α содержит прямую KN и параллельна прямой BC.

а) Докажите, что плоскость α параллельна прямой SA.

б) Найдите угол между плоскостями α и SBC.

а) Построим прямую MN параллельно CB и прямую KP параллельно CB, Плоскость NMP параллельна BC и содержит NK, таким образом NMP искомая плоскость α. По теореме о пропорциональных отрезках имеем: Таким образом, PM параллельна SA, значит, SA параллельна α.

б) Заметим, что NM параллельна DA и SA параллельна PM , тогда Таким образом, угол между плоскостью и плоскостью SBC равен углу между плоскостями SBC и SDA. Тогда искомый угол где F — середина BC, а O — цетнр основания пирамиды. Таким образом, а

Ответ:

Основание прямой треугольной призмы ABCA₁B₁C₁ — треугольник ABC, в котором AB = AC = 8, а один из углов равен 60°. На ребре AA₁ отмечена точка P так, что AP : PA₁ = 1 : 2. Расстояние между прямыми AB и B₁C₁ равно

а) Докажите, что основания высот треугольников ABC и PBC, проведенных к стороне BC, совпадают.

б) Найдите тангенс угла между плоскостями ABC и CBP.

а) Заметим, что так как треугольник ABC равнобедренный, а один из его углов равен 60°, треугольник ABC — равносторонний и, значит, призма — правильная. В треугольнике PBC проведём высоту PH, по теореме о трёх перпендикулярах её проекция AH будет являться высотой треугольника ABC. Тем самым, основания высот треугольников ABC и PBC, проведенных к стороне BC, совпадают.

б) Прямые AB и B₁C₁ скрещивающиеся и лежат в параллельных плоскостях ABC и A₁B₁C₁. Следовательно, расстояние между ними равно расстоянию между этими плоскостями, то есть боковому ребру призмы. Тогда: По доказанному в п. а) угол PHA является линейным углом угла между плоскостями ABC и CBP. Следовательно,

Ответ:

Дана правильная четырехугольная призма ABCDA₁B₁C₁D₁. На ребре BB₁ отмечена точка Q такая, что BQ : QB₁ = 2 : 7. Плоскость α проходит через точки A и Q параллельно прямой BD. Эта плоскость пересекает ребро CC₁ в точке M.

б) Найдите площадь сечения, если AA₁ = 18.

а) Пусть сечение пересекает ребро DD₁ в точке R. Тогда прямая QR лежит в плоскости BB₁D₁D и параллельна BD. Пусть T — центр основания, а S — точка пересечения AM и QR. Треугольники AST и AMC подобны с коэффициентом подобия 2, откуда

б) Заметим, что далее

следовательно, AQMR — ромб. Имеем тогда

В правильной четырехугольной пирамиде PABCD каждое ребро равно 12. На ребре PC отмечена точка K так, что PK : KC = 1 : 3.

а) Докажите, что линия пересечения плоскостей ABK и PCD параллельна плоскости ABC.

б) Найдите площадь сечения пирамиды плоскостью ABK.

а) Проведем в плоскости PCD прямую KT, параллельную CD. Поскольку то и Поэтому точки A, B, K, T лежат в одной плоскости и искомое переечение плоскостей — прямая KT. Она параллельна плоскости основания пирамиды, поскольку параллельна CD.

б) Рассмотрим трапецию ABKT. В ней Очевидно, что треугольник PKT равносторонний, поэтому

По теореме косинусов из треугольника BPK имеем

Опустим теперь в трапеции высоту KH на основание AB. Тогда и по теореме Пифагора для треугольника BKH получаем

Ответ:

а) Докажите, что плоскость Ω проходит через вершину F₁.

б) Найдите расстояние от точки А до плоскости Ω, если АВ = 2, АА₁ = 4.

а) Проведем прямую в плоскости параллельно Тогда и значит лежит на диагонали Поэтому плоскость содержит прямую а значит и точку

б) Теперь найдём расстояние от точки А до плоскости Ω: поскольку перпендикуляр к будет лежать в плоскости и поэтому будет перпендикулярен как и все, что лежит в этой плоскости.

Ответ: б)

В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 6, а боковое ребро SA = 7. На рёбрах CD и SC отмечены точки N и K соответственно, причём DN : NC = SK : KC = 1 : 2. Плоскость α содержит прямую KN и параллельна прямой BC.

а) Докажите, что плоскость α параллельна SA

б) Найдите угол между плоскостями и SBC.

а) Построим прямую MN параллельно CB и KP параллельно CB, Плоскость NMP параллельна BC и содержит NK, таким образом NMP искомая плоскость α. По теореме о пропорциональных отрезках имеем: Таким образом, PM параллельна SA, значит, SA параллельна α.

б) Заметим, что NM параллельна DA и SA параллельна PM , тогда SDA || следовательно, угол между и плоскость SBC равен углу между плоскостями SBC и SDA. Тогда искомый угол равен двум углам FSO, где F — середина BC, а O — основание высоты пирамиды. Таким образом,

Тогда искомый угол

Ответ:

Аналоги к заданию № 541379: 541823 Все

Дана правильная треугольная призма ABCA₁B₁C₁ в которой AB = 6 и AA₁ = 3. Точки O и O₁ являются центрами окружностей, описанных около треугольников ABC и A₁B₁C₁ cответственно. На ребре CC₁ отмечена точка M такая что CM = 1.

а) Докажите, что прямая OO₁ содержит точку пересечения медиан треугольника треугольника ABM.

б) Найдите объем пирамиды ABMC₁.

а) Пусть точка K — середина ребра AB, а Q — такая точка на MK, что MQ : QK = 2 : 1. Тогда Q — точка пересечения медиан треугольника ABM, поскольку делит его медиану MK в отношении 2 : 1, считая от вершины. Очевидно, что проекцией отрезка MK на плоскость ABC будет отрезок CK, поэтому, так как О является точкой пересечения медиан треугольника ABC и делит CK в отношении 2 : 1, точка Q будет проектироваться в эту точку. Прямая OO₁ и плоскость ABC перпендикулярны, следовательно, Что и требовалось доказать.

б) Вычислим объем пирамиды ABMC₁:

Ответ: б)

Дана правильная треугольная призма ABCA₁B₁C₁, в которой AB = 1 и AA₁ = 3. Точки O и O₁ являются центрами окружностей, описанных около треугольников ABC и A₁B₁C₁ cответственно. На ребре CC₁ отмечена точка M такая что CM = 2.

а) Докажите, что прямая OO₁ содержит точку пересечения медиан треугольника треугольника ABM.

б) Найдите объем пирамиды ABMC₁.

б) Вычислим объем пирамиды ABMC₁:

Ответ: б)

Аналоги к заданию № 548801: 548808 Все

В правильной восьмиугольной призме ABCDEFGHA₁B₁C₁D₁E₁F₁G₁H₁ сторона основания AB равна а боковое ребро AA₁ равно 6. Ha pe6pe CC₁ отмечена точка M так, что Плоскость параллельна прямой H₁E₁ и проходит через точки M и A.

а) Докажите, что сечение данной призмы плоскостью α — равнобедренная трапеция.

б) Найдите объем пирамиды, вершиной которой является точка F₁, а основанием — сечение данной призмы плоскостью α.

а) Рассмотрим ребра фигуры: E₁H₁, F₁G₁, FG и AD₁ параллельны, значит, AD принадлежит плоскости Точка N принадлежит ребру BB₁, поэтому

значит стороны MN, CB, FG и EH₁ параллельны. Таким образом, MN принадлежит плоскости

Соединим точки AMND — точки сечения призмы — плоскостью

Плоскость ADMN параллельна E₁H₁, следовательно, стороны плоскости AD и MN также параллельны.

Треугольники MCD и NBA равны, так как стороны CD и AB, MC и NB одинаковы, как и углы MCD и NBA. Тогда стороны плоскости MD и AN равны, а значит сама плоскость ANMD является равнобедренной трапецией.

Точка P лежит на пересечении прямых AD и CF, отсюда следует, что CFF₁ пересекает плоскость

причем MP — место пересечения данных плоскостей.

Плоскости CFF₁ и ABC перпендикулярны, так как по условию ребро FF₁ перпендикулярно к основанию правильной призмы. Отрезки FC и AD, AD и FF₁ перпендикулярны, следовательно, AD перпендикулярен к плоскости CFF₁, таким образом, перпендикулярна к плоскости CFF₁.

Отрезок AD лежит в плоскости основания, все боковые ребра перпендикулярны к основанию. Высота из точки F₁ на попадает на отрезок MP. Так как CD перпендикулярно к AD, то MP также перпендикулярно к AD по правилу о трех перпендикулярах.

Сторона Площадь плоскости будет равна:

Выразим площадь MF₁P через другие площади и найдем её значение:

Посчитаем значение площади трапеции AMND:

Вычислим объем пирамиды F₁AMND:

Ответ:

Видео:Радиус основания цилиндра равен 26, а его образующая равна 9... Найдите площадь сечения.Скачать

Как посчитать объем цилиндра

Видео:ЕГЭ БАЗА 16 номер Радиус основания цилиндра равен 15, а его образующая равна 14Скачать

Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

радиус r и высоту h цилиндра
диаметр d и высоту h цилиндра
площадь основания S_o и высоту h цилиндра
площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3

Зная диаметр d и высоту h

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ ( 1 /₂) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3

Зная площадь основания S_o и высоту h

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см 2 , то:

V = 10 ⋅ 5 = 50 см 3

Зная площадь боковой поверхности S_b и высоту h

Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см 2 , то:

V = 30 2 / _{4 ⋅ 3.14⋅ 5} = 900 /_62.8 = 14.33 см 3

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Диаметр окружности основания цилиндра 20 образующая 28

Чтобы купить курс,
пожалуйста, войдите
или зарегистрируйтесь

Быстрая регистрация

Математика (проф. ур.) (Вариант 1)

Приобретите наш курс

Для продолжения просмотра купите полный курс
наших видеоуроков

Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно

а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости.

б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.

Сразу отметим, что в окружности радиуса R расстояние от центра до хорды (то есть до середины хорды) длиной равно Поэтому расстояния от центров оснований до хорд равны 5 и 12.

а) Пусть A и — середины хорд, B — проекция на другое основание цилиндра. Тогда поэтому следует выбирать знак , что как раз и означает, что хорды лежат по разные стороны от центров оснований, поэтому центры лежат по разные стороны от плоскости.