Наиболее распространёнными графическими представлением анализов гранулометрического состава горных пород (табл. 3.2) являются гистограммы, циклограммы, графики треугольники и интегральные (кумулятивные) кривые.
Результаты гранулометрического анализа горных пород
| № анализа | Размер фракций, мм / Процентное содержание частиц, % | |||||||
| 2–1 | 1–0,5 | 0,5–0,25 | 0,25–0,1 | 0,1–0,05 | 0,05–0,01 | 0,01–0,005 | 0,005–0,001 | Менее 0,001 |
| − | − |
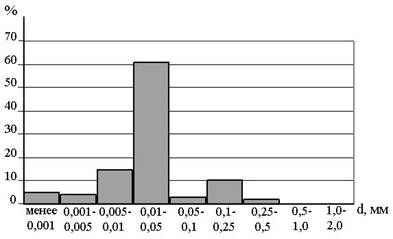
Гистограмма – столбчатая диаграмма, один из видов графического изображения статистического распределении каких-либо величин по количественному признаку. Гистограмма представляет собой совокупность смежных прямоугольников, построенных на прямой линии.
Для изображения на гистограмме гранулометрического состава горных пород на вертикальной оси откладывают процентное содержание фракций, а на горизонтальной оси – произвольно выбранные равные отрезки.
На отрезках, соответствующих каждой фракции, строится как на основании прямоугольник высотой, равной процентному содержанию частиц во фракции.
Гистограмма, изображающая гранулометрический состав горной породы анализа № 1 представлена на рис. 3.1.
Рис. 3.1. Гистограмма гранулометрического состава пород анализа №1
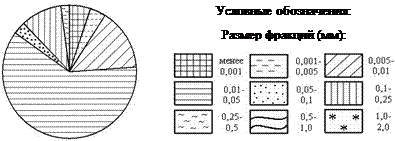
При построении циклограмм, характеризующих гранулометрический состав горных пород, вычерчивается окружность произвольного радиуса. Площадь окружности принимается за 100 %. Величина отдельной фракции показывается в виде сектора, площадь которого пропорциональна ее процентному содержанию. Сектора заштриховываются в соответствии с принятыми к фракциям условным обозначениям.
Циклограмма, изображающая гранулометрический состав горной породы анализа № 1 представлена на рис. 3.2.
Рис. 3.2. Циклограмма гранулометрического состава пород анализа №1
Графические изображения результатов гранулометрического анализа в виде гистограмм и циклограмм имеют существенный недостаток, который заключается в невозможности изображения результатов массовых определений гранулометрического состава на одной гистограмме или циклограмме.
График-треугольник (см. приложение 1) представляет собой равносторонний треугольник, каждая сторона которого разделена на 100 равных частей. Если принять, что каждая из вершин треугольника отражает нулевое содержание одной из основных фракций, тогда по углам треугольника будет отмечаться стопроцентное содержание этих фракций. Линии, параллельные сторонам, будут соответствовать процентному содержанию той или иной фракции, а это значит, что точка внутри треугольника будет соответствовать составу породы.
По положению точки внутри графика – треугольника можно судить о распределении фракции в горной породе и в зависимости от этого дать определение породы.
График-треугольник гранулометрического состава горной породы анализа № 1 представлен на рис. 3.3.
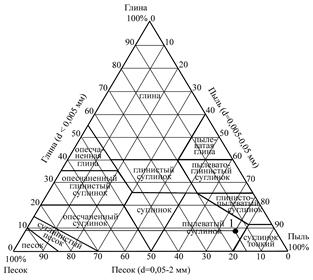 |
Рис. 3.3. График-треугольник гранулометрического состава горной породы анализа № 1
Анализируя расположение точки 1 внутри графика – треугольника, можно сделать вывод, что рассматриваемая порода относится к пылеватым суглинкам.
Интегральные (кумулятивные) кривые гранулометрического состава строятся в прямоугольной системе координат в полулогарифмическом масштабе (когда по одной оси задается логарифмический масштаб, а по другой – линейный).
Использование полулогарифмического масштаба вызвано тем, что при гранулометрическом анализе частицы подразделяются на фракции, размеры которых убывают в геометрической прогрессии. По оси абсцисс откладываются логарифмы диаметров фракций частиц, а по оси ординат – содержание данной фракции в породе в процентах.
Для удобства определения логарифмов диаметров частиц переводят эти размеры из миллиметров в микроны для того, чтобы не получать отрицательных логарифмов (табл. 3.3).
Исходные данные для построения кумулятивной кривой
гранулометрического состава горных пород
| Фракция | Сумма фракций | Расчетные значения | |||
| Диаметр частиц, мм | Содержание частиц, % | Диаметр частиц, мм | Содержание частиц, % | Логарифм диаметра частиц, lg d | Расстояние от начала оси абсцисс, см |
| 0,001 | |||||
| 0,001–0,005 | 0,7 | 2,3 | |||
| 0,005–0,01 | 1,0 | 3,3 | |||
| 0,01–0,05 | 1,7 | 5,6 | |||
| 0,05–0,1 | 2,0 | 6,6 | |||
| 0,1–0,25 | 2,4 | 7,9 | |||
| 0,25–0,5 | 2,7 | 8,9 | |||
| 0,5–1,0 | 3,0 | 9,9 | |||
| 1,0–2,0 | 3,3 | 12,0 |
Для построения логарифмической шкалы по оси абсцисс от начальной точки в некотором масштабе откладываются отрезки, равные десятичным логарифмам ряда чисел. Если отложено число, равное lg d, то около соответствующей точки ставится d. Около начальной точки должна стоять пометка 1, т.к. lg 1 = 0. Таким образом, на логарифмической шкале расстояние от пометки 1 до пометки d равно в выбранном масштабе lg α.
Так как lg (10d) = 1+ lg d, то пометки на логарифмической шкале на участке от 10 до 100 будут в точности соответствовать пометкам на участке от 1 до 10. Это же рассуждение может быть проведено и для других участков шкалы. Поэтому, для изображения чисел от 1 до 100 на логарифмической оси требуется увеличить длину оси всего в два раза по сравнению с осью, размеченной от 1 до 10.
При построении кумулятивных кривых гранулометрического состава горных пород, диапазон изменений диаметра частиц превышает их порядок (dмин = 1 мк, dмах = 2000 мк). Таким образом, на оси абсцисс необходимо отобразить числа от 1 до 2000. Целесообразно разделить ось на 4 декады, включающие диаметры 1–10 мк, 10–100 мк, 100–1000 мк и 1000–2000 мк. Примем длину оси равной 12 см, тогда на одну декаду будет приходиться 3 см. Соответственно, деление 5 должно стоять на расстоянии L = lg5 × 3 = 2,1 см от начала оси абсцисс, деление 50 – на расстоянии L = lg50 × 3 = 5,1 см, деление 500 – на расстоянии L = lg500 × 3 = 8,1 см.
Процентное содержание по оси ординат откладывают, начиная с самой мелкой фракции. Для каждой последующей фракции величину ординаты получают последовательным суммированием данных для предыдущих размеров, т.е. к процентному содержанию предыдущей фракции прибавляют процентное содержание следующей и т.д. (см. табл. 3.3).
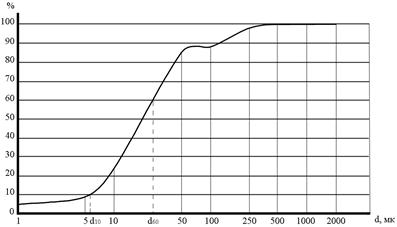
Таким образом, каждая точка графика дает суммарное количество частиц данного размера и размеров, меньших, чем этот размер. По пересечению диаметров частиц строят кривую, которая называется кумулятивной кривой (рис. 3.4).
Кумулятивные кривые позволяют определить действующий или эффективный и контролирующий диаметры частиц и вычислить на их основе коэффициент неоднородности, показывающий степень отсортированности пород.
Рис. 3.4. Кумулятивная кривая гранулометрического состава горной породы
Коэффициент неоднородности (Кн) представляет собой отношение величины контролирующего диаметра частиц (d60) к величине действующего их диаметра (d10):
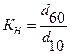
Действующим (эффективным) диаметром частиц является такой диаметр, меньше которого в породе содержится 10 % частиц.
Контролирующим диаметром называется диаметр, меньше которого в породе 60 % частиц.
Для определения действующего и контролирующего диаметров частиц, из точек на оси ординат, соответствующих 10 и 60 % их содержанию проводятся линии, параллельные оси абсцисс до пересечения с кумулятивной кривой. Из точек пересечения опускаются перпендикуляры на ось абсцисс (см. рис. 5.4) и определяются значения диаметров частиц. Значение коэффициента неоднородности определяется с точностью до запятой.
Для определения диаметров частиц необходимо определить расстояние от места пересечения соответствующих перпендикуляров до начала оси абсцисс (L). Диаметр частиц определится из выражения lg d = L/3.
Коэффициент неоднородности не может быть меньше единицы и практически не бывает больше 200. Чем меньше его величина − тем однороднее порода. Принято, что при Кн = 5 порода считается однородной и для нее характерно ламинарное движение подземных вод. Если Кн > 5, то порода считается неоднородной по гранулометрическому составу, и подземные воды в ней имеют турбулентный характер движения.
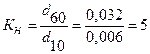
Так как Кн > 5, то горная порода по гранулометрическому составу считается неоднородной, и подземные воды в ней имеют турбулентный характер движения.
- Определение гранулометрического состава грунта – Треугольник Ферре
- Как самостоятельно исследовать гранулометрический состав почвы?
- Треугольник Ферре как пользоваться?
- К вопросу о построении треугольных диаграмм в программе Microsoft Exel при изучении пород-коллекторов Штокмановского месторождения Текст научной статьи по специальности « Математика»
- Аннотация научной статьи по математике, автор научной работы — Крюкова Ирина Борисовна
- Похожие темы научных работ по математике , автор научной работы — Крюкова Ирина Борисовна
- Текст научной работы на тему «К вопросу о построении треугольных диаграмм в программе Microsoft Exel при изучении пород-коллекторов Штокмановского месторождения»
- 📹 Видео
Видео:09 Фаз диагр двухкомп сист 1 принципы и мех смесьСкачать
Определение гранулометрического состава грунта – Треугольник Ферре
Определение гранулометрического состава грунта — первый шаг к выбору типа фундамента для строительства жилых и промышленных объектов, в ходе которого будут исследованы пучинистые, дренажные, просадочные, несущие и другие особенности почвы. Кроме того, процедура позволяет узнать пропорции химических и минералогических веществ в структуре земли, что важно и для дачников.
Специалистами рекомендуется проводить профессиональное геологическое исследование, которое предоставляет возможность получить максимально верные данные. В случае отсутствия средств или возможности для заказа геологической группы, можно провести исследование самостоятельно, однако итоговые результаты нельзя считать достоверными, хотя дадут общее понимание о составе грунта на исследуемом участке.
Видео:Лекция «Диаграмма состояния двухкомпонентных сплавов»Скачать

Как самостоятельно исследовать гранулометрический состав почвы?
Если в вашей местности нет квалифицированных геологов или их услуги слишком дорогие для ваших финансовых возможностей, можно воспользоваться несколькими известными методиками для ориентировочной оценки грунта.
Основные способы исследования почвы:
- ситовой;
- с помощью ареометра;
- пипеточный;
- метод двойного отмучивания по Сабанину — анализируется свободное падение частиц грунта в воде;
- метод Рутковского (набухание глиняных частиц в воде, осаждение на дно емкости)
Мы приведем самый простой и распространенный, в том числе и среди дачников. Описываемый ниже нами способ похож на упрощенный метод определения состава грунтов Рутковского.
Отличить песок от глины сможет любой дачник или начинающий строитель — в некоторых случаях достаточно пройтись по такому грунту. Как правило, глина налипает на подошву обуви, а песок осыпается. Для того, чтобы приступить к обработке или застройке земли, этих наблюдений, конечно, недостаточно. Так возникает необходимость в исследовании механического состава земли.
Приведенный нами способ определения гранулометрического состава заключается в анализе времени, которое занимает процесс оседания различных по весу частиц грунта на дно емкости, заполненной водой, а также определении процентного соотношения глины / ила/ песка.
- Возьмите со своего участка образец грунта, в котором вы хотите определить процентное соотношение глиняных, песчаных и пылеватых частиц, а лучше несколько проб грунта с разных частей участка (по пятну застройки, то есть где вы планируете строить дом). Глубина бурения грунта для взятия проб – от 4 метров (чем тяжелее дом, тем глубже стоит посмотреть).
- Поместите образец грунта в стеклянную колбу или литровую банку. Грунта должно быть чуть меньше, чем половина.
- В емкость налейте пару капель средства для мытья посуды, затем долейте до самого верха воды, оставляем где-то 2,5 см от края для воздуха, чтобы можно было смешать образец грунта с водой.
- Закройте банку крышкой и с усилием трясем смесь 3-5 минут.
- Вычислить количество частиц песка можно уже ч/з пару минут — он быстро оседает на дно емкости. Можете сразу отметить уровень оседания маркером.
- Вычислить количество пылеватых частиц ила можно не ранее интервала в 2-3 часа. Вы заметите, как он уляжется на ранее осевший слой песка — нанесите маркером на емкость вторую метку.
- Определить долю глины удастся лишь как минимум через сутки, как максимум — по истечению 2-5 дней, (банку не трогайте). Когда вода станет менее мутной, а грунт «усядется», нанесите последнюю метку на банку.
Далее гранулометрический состав почвы определяется исходя от вашего образца:
• высота от дна банки до третьей метки принимается за 100%;
• определяем долю каждого слоя из осадков и переносим итоговые числа в форму, используя метод треугольных координат – пользуемся треугольником Ферре;
Видео:Морфология почв. Определение гранулометрического состава.Скачать

Треугольник Ферре как пользоваться?
Использование треугольника Ферре — самый простой и несложный метод проведения гранулометрического анализа почвы, содержащихся во взятой пробе.
Необходимо нанести на сетку треугольника полученные числовые значения основных составляющих взятого образца в %: ил или пылеватые частицы, песок и глина.
После нанесения всех меток на треугольник можно понять, что представляет собой взятый образец земли. Пример: отмечаем на сетке полученные опытным путем значения: 30% — песок, 30% — ил, 40% — глина. Итог — глинистый суглинок.
Следует повторить исследование грунта с другими образцами грунта, взятыми по пятну застройки.
Отметим еще раз, что такой способ подходит для приблизительного определения содержания грунта в толще участка. И ни в коем случае не заменяет полноценные инженерно-геологические исследования. Но вполне можно рассмотреть такой вариант анализа гранулометрического состава почвы в качестве «лучше так, чем ничего».
Если вы смогли определить гранулометрический состав грунта, самое время воспользоваться онлайн-калькулятором расчета фундамента, для того чтобы узнать допустимые параметры несущих элементов.
Видео:Диаграмма Максвелла-КремоныСкачать

К вопросу о построении треугольных диаграмм в программе Microsoft Exel при изучении пород-коллекторов Штокмановского месторождения Текст научной статьи по специальности « Математика»
Видео:практическая 7 определение гранулометрического состава порошкаСкачать

Аннотация научной статьи по математике, автор научной работы — Крюкова Ирина Борисовна
Рассматривается метод построения гранулометрического треугольника в программе Microsoft Exel через замену треугольных координат на прямоугольные.
Видео:ДИАГРАММА СОСТОЯНИЯ ЖЕЛЕЗО-ЦЕМЕНТИТ, железо-углерод, Fe+Fe3CСкачать
Похожие темы научных работ по математике , автор научной работы — Крюкова Ирина Борисовна
Видео:Диаграмма состояния сплавов системы «железо-углерод»Скачать

Текст научной работы на тему «К вопросу о построении треугольных диаграмм в программе Microsoft Exel при изучении пород-коллекторов Штокмановского месторождения»
К ВОПРОСУ О ПОСТРОЕНИИ ТРЕУГОЛЬНЫХ ДИАГРАММ В ПРОГРАММЕ MICROSOFT EXEL ПРИ ИЗУЧЕНИИ ПОРОД-КОЛЛЕКТОРОВ ШТОКМАНОВСКОГО МЕСТОРОЖДЕНИЯ
И.Б. Крюкова (ООО «Газпром ВНИИГАЗ»)
Одной из удобных и наглядных форм представления результатов экспериментов является треугольная диаграмма, позволяющая показать несколько анализов на одном чертеже. Этот метод популярен в гранулометрии, геохимии, при анализе трехфазных сред и т.д. Однако, когда мы имеем дело с большим количеством данных, например, по результатам гранулометрического анализа пород, возникает проблема их автоматической обработки. Для этого удобно было бы воспользоваться программой Microsoft Exel, но в стандартном наборе возможных графиков отсутствуют треугольные диаграммы.
Эту проблему можно обойти, если при построении перейти от треугольных координат к стандартным прямоугольным путем замены переменных, и затем воспользоваться мастером диаграмм Microsoft Exel, выбрав тип диаграммы «точечная». Таким образом, программа будет наносить точки на стандартное поле в привычных координатах (x, y), но эти точки не будут выходить за рамки равностороннего треугольника, и их координаты будут в точности соответствовать исходным значениям на треугольных осях.
В исходных данных для треугольных диаграмм координаты каждой точки заданы в виде трех чисел (a; b; c), сумма которых равна 100:
Нужно отметить, что третья координата является номинальной и на самом деле на положение точки не влияет, так как рассчитывается из первых двух: еі = 100 — аі- Ь¡. Поэтому для замены переменных необходимо установить соответствие треугольных координат (а;; Ь) стандартным прямоугольным (х; уі).
Рассмотрим рис. 1. Мы видим треугольную диаграмму СВА и нанесенную на нее точку с координатами (а; Ь). На эту треугольную диаграмму наложены стандартные прямоугольные осиX, У, в проекции на которые координаты данной точки принимают значения (х; у) соответственно. Необходимо найти два уравнения замены переменных: х = /1(а, Ь) и у = /2(а, Ь).
ai + bi + c i = 100, i = 1. n, где n — количество точек.
Рис. 1. Схема перевода треугольных координат в прямоугольные
Из данного построения видно, что ось ординат Y полностью совпадает по направлению с осью, с которой снимается треугольная координата b, и эти координаты у данной точки полностью совпадают, т.е. первое уравнение замены переменной выглядит очень просто:
Для нахождения координаты x рассмотрим заштрихованные треугольники. Они подобны, и нам известны в них все углы (90°, 30° и 60°). В результате несложных геометрических вычислений полу-20 + b тт
чим выражение x = —р—. Но это еще не окончательный результат, так как максимальные значения V3
координат по прямоугольным и треугольным осям должны быть одинаковы (и равны 100), а в нашем построении длины отрезков осей X и Y от 0 до 100 соотносятся как высота и длина стороны равнобедренного треугольника, т.е. ^2-. Таким образом, учитывая поправочный коэффициент, получаем
Имея уравнения (1) и (2), мы можем без труда пересчитать в программе Microsoft Exel треугольные координаты на прямоугольные для любого, даже очень большого, количества точек и затем в прямоугольных координатах построить точечную диаграмму, которая будет выглядеть как треугольная.
На рис. 2 показан пример построения гранулометрического треугольника по результатам гранулометрического анализа керна, поднятого из скв. 7 Штокмановского месторождения, из интервала 1952-1997 м, пласт Ю0.
Рис. 2. Пример построения треугольной диаграммы
Исходные данные находятся в столбцах А, В, С и D. В ячейку Е2 нужно ввести формулу пересчета первой координаты (х): D2 + С2/2 и распространить ее на весь столбец. В ячейки F2-F16 (координата у) копируется столбец С. Далее с помощью мастера диаграмм выбираем «точечную диаграмму» и строим график на выборке (х, у).
Чтобы диаграмма выглядела как треугольная, ее необходимо подредактировать: в «параметрах диаграммы» сделать невидимой ось У и вручную с помощью панели инструментов «Рисование» нарисовать равнобедренный треугольник с основанием на оси абсцисс.
Данный метод может применяться не только для построения гранулометрического треугольника, но и для аналогичного вида треугольных диаграмм, например, при анализе минерального состава пород и других.
📹 Видео
Определение гранулометрического состава грунта ситовым методомСкачать

Исследование гранулометрического состава при помощи лазерной дифракцииСкачать

Фазовые диаграммы. Тройная точка. Критическое состояние вещества. 10 класс.Скачать

Диаграмма ИсикавыСкачать

Потенциальная диаграммаСкачать

ДИАГРАММА ЖЕЛЕЗО-УГЛЕРОД [МАТЧАСТЬ]Скачать
![ДИАГРАММА ЖЕЛЕЗО-УГЛЕРОД [МАТЧАСТЬ]](https://i.ytimg.com/vi/L1VZ5rbqL7Q/0.jpg)
6-1. Грунтоведение. Строение грунтов. Гранулометрический и микроагрегатный составы.Скачать

Лекция 10. I-d диаграмма и параметры влажного воздухаСкачать
Диаграммы Пурбе: как ими пользоваться на примере химии хрома и марганца.Скачать

Гранулометрический анализ в археологии и палеонтологии.Скачать

Диаграмма Максвелла-КремоныСкачать

Диаграмма сплавов Железо углерод ЛекцияСкачать