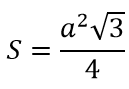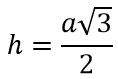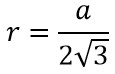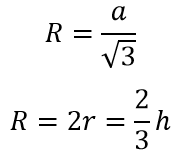Диагональ правильного треугольника формула

Равносторонний или правильный треугольник — треугольник, у которого три стороны равны. Все углы равностороннего треугольника равны.

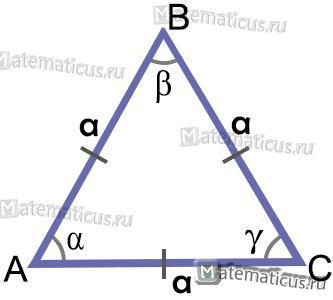
Равносторонним треугольником называется такой треугольник, у которого все стороны равны, то есть АВ = ВС = АС (рис. 1)

Свойства равностороннего (правильного) треугольника

1. Все углы равностороннего треугольника равны по 60°

∠А=∠С=∠В=60°

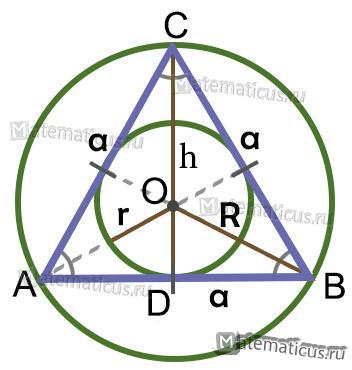
1. Биссектрисы треугольника являются медианами и высотами, то есть равны и точка их пересечения, является центром вписанной окружности (рис. 2).

Из (рис. 2) обозначения:

h — высота=биссектриса=медиана

R — радиус описанной окружности
r — радиус вписанной окружности
a — стороны правильного треугольника

Формула периметра равностороннего треугольника:

P=3·a

Формула площади правильного треугольника:

Формула высоты (или медианы или биссектрисы) равностороннего треугольника:

Радиус вписанной окружности в равносторонний треугольник:

Радиус описанной окружности в равносторонний треугольник:

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.6 / 5. Количество оценок: 5

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Диагональ треугольника – формула

Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Треугольник

Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:

Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.

Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной. Значит, диагонали треугольника не существует

Рис. 1. Три медианы в треугольнике.

Видео:как найти диагональ.Скачать

Прямоугольник

Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.

Диагональ прямоугольника или квадрата всегда:

• Делит фигуру на две равных прямоугольных треугольника.
• В полученных треугольниках диагональ будет являться гипотенузой
• Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора

Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.

При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.

Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.

Видео:Теорема Пифагора для чайников)))Скачать

Многоугольник

На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.

Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.

Рис. 2. Диагонали многоугольника.

В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.

Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.

Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.

Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.

Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:

$P=<n(n-3)over>$ – где n это число сторон многоугольника.

Проверим для квадрата:

Рис. 3. Диагонали квадрата.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Что мы узнали?

Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.

Видео:Формулы равностороннего треугольника #shortsСкачать

Свойства равностороннего треугольника: теория и пример задачи

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:Как найти площадь треугольника без формулы?Скачать

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Видео:Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Видео:Как найти диагональ... Диагональни топишСкачать

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

💥 Видео

Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Свойства правильного шестиугольника. Сравнение площадей. Разбор задачи из стереометрии.Скачать

151 Диагонали правильного шестиугольника пересекаются в центре его описанной окружности (268)Скачать

👉 ФОРМУЛА ГЕРОНА. Площадь треугольника #shortsСкачать

Геометрия Равносторонний треугольникСкачать

Площадь квадрата через диагональ 📐 Полезный файлик в комментариях)Скачать

№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать

Нахождение стороны прямоугольного треугольникаСкачать

ПРАВИЛЬНАЯ диагональ! Самый простой и точный способ.Разметка фундаментаСкачать

Диагонали правильных многоугольниковСкачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать