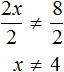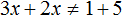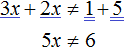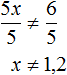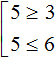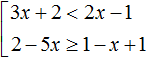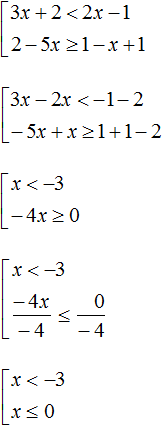Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
- Что такое множества, где и как они применяются
- Какие бывают множества
- Подмножества
- Решить задачу на множества самостоятельно, а затем посмотреть решение
- Основные числовые множества
- Операции над множествами: объединение, пересечение, разность, декартово произведение
- Операция объединения множеств
- Операция пересечения множеств
- Разность множеств
- Выполнить операции над множествами самостоятельно, а затем посмотреть решение
- Операция декартова произведения множеств
- Выполнить операции над множествами самостоятельно, а затем посмотреть решение
- Свойства операций над множествами
- Решение различных задач на множества
- Треугольники, множества и алгебра
- Как перечислить все треугольники?
- Причем тут алгебра?
- Почему это все бесполезно?
- В заключение
- Операции над множествами
- Пересечение множеств
- Объединение множеств
- Решение неравенств, содержащих знак ≠
- Решение совокупностей неравенств
- 🎥 Видео
Видео:Множества. Операции над множествами. 10 класс алгебраСкачать

Что такое множества, где и как они применяются
В математике понятие множества является одним из основных, фундаментальным, однако единого определения множества не существует. Одним из наиболее устоявшихся определений множества является следующее: под множеством понимают любое собрание определённых и отличных друг от друга объектов, мыслимых как единое целое. Создатель теории множеств немецкий математик Георг Кантор (1845-1918) говорил так: «Множество есть многое, мыслимое нами как целое».
Ели ли Вы сегодня обед? Сейчас станет известна страшная тайна. Обед является множеством. А именно, множеством блюд, из которых он состоит. В нём (как правило) нет одинаковых блюд, и во множестве все элементы должны быть разными. А, если на обед у Вас был тот же самый салат, что и на завтрак, то этот салат является пересечением множеств «Обед» и «Завтрак».
Взгляните на книгу, лежащую на столе или стоящую на полке. Она является множеством страниц. Все страницы в ней отличаются друг от друга, по меньшей мере номерами.
А улица, на которой Вы живёте? Она является собранием многих разных объектов, но обязательно есть множество домов, расположенных на этой улице. Поэтому множество домов является подмножеством множества «Улица».
Итак, мы рассмотрели не только примеры множеств, но и пример операции над множествами — пересечение, а также отношение включения подмножества во множество. Все эти понятия будем рассматривать подробно на этом уроке.
Но пока ещё один пример практического рассмотрения множеств.
Множества как тип данных оказались очень удобными для программирования сложных жизненных ситуаций, так как с их помощью можно точно моделировать объекты реального мира и компактно отображать сложные логические взаимоотношения. Множества применяются в языке программирования Паскаль и один из примеров решения мы ниже разберём.
Пример 0 (Паскаль). Существует набор продуктов, продаваемых в нескольких магазинах города. Определить: какие продукты есть во всех магазинах города; полный набор продуктов в городе.
Решение. Определяем базовый тип данных Food (продукты), он может принимать значения, соответствующие названиями продуктов (например, hleb). Объявляем тип множества, он определяет все подмножества, составленные из комбинаций значений базового типа, то есть Food (продукты). И формируем подмножества: магазины «Солнышко», «Ветерок», «Огонёк», а также производные подмножества: MinFood (продукты, которые есть во всех магазинах), MaxFood (полный набор продуктов в городе). Далее прописываем операции для получения производных подмножеств. Подмножество MinFood получается в результате пересечения подмножеств Solnyshko, Veterok и Ogonyok и включает те и только те элементы этих подмножеств, которые включены в каждое их этих подмножеств (в Паскале операция пересечения множеств обозначается звёздочкой: A * B * C, математическое обозначение пересечения множеств дано далее). Подмножество MaxFood получается в результате объединения тех же подмножеств и включает элементы, которые включены во все подмножества (в Паскале операция объединения множеств обозначается знаком «плюс»: A + B + C, математическое обозначение объединения множеств дано далее).
Код PASCAL
Видео:Множества и операции над нимиСкачать

Какие бывают множества
Объекты, составляющие множества — объекты нашей интуиции или интеллекта — могут быть самой различной природы. В примере в первом параграфе мы разобрали множества, включающие набор продуктов. Множества могут состоять, например, и из всех букв русского алфавита. В математике изучаются множества чисел, например, состоящие из всех:
— натуральных чисел 0, 1, 2, 3, 4, .
— чётных целых чисел
и т.п. (основные числовые множества рассмотрены в соответствующем параграфе этого материала).
Объекты, составляющие множество, называются его элементами. Можно сказать, что множество — это «мешок с элементами». Очень важно: в множестве не бывает одинаковых элементов.
Множества бывают конечными и бесконечными. Конечное множество — это множество, для которого существует натуральное число, являющееся числом его элементов. Например, множество первых пяти неотрицательных целых нечётных чисел 
Если M — множество, а a — его элемент, то пишут: a∈M , что означает » a принадлежит множеству M«.
Из первого (нулевого) примера на Паскале с продуктами, которые есть в тех или иных магазинах:
что означает: элемент «hleb» принадлежит множеству продуктов, которые есть в магазине «VETEROK».
Существуют два основных способа задания множеств: перечисление и описание.
Множество можно задать, перечислив все его элементы, например:
Перечислением можно задать только конечное множество. Хотя можно сделать это и описанием. Но бесконечные множества можно задать только описанием.
Для описания множеств используется следующий способ. Пусть p(x) — некоторое высказывание, которое описывает свойства переменной x , областью значений которых является множество M . Тогда через M = <x | p(x)> обозначаентся множество, состоящее из всех тех и только тех элементов, для которых высказывание p(x) истинно. Это выражение читается так: «Множество M , состоящее из всех таких x , что p(x) «.
означает множество корней уравнения x² — 3x + 2 = 0 , т. е. множество . Это конечное множество.
А следующим описанием задаётся множество всех целых чисел больше 5:
это множество является бесконечным.
Описанием предпочтительно задавать и конечные множества, в которых очень много элементов, например, множество всех натуральных чисел от 2 до 22³ :
Множество, не содержащее ни одного элемента, называется пустым и обозначается знаком ∅.
Множество может состоять из одного элемента. Необходимо различать элемент a и множество <a> , содержащее только один элемент a , хотя бы потому, что допускаются множества, элементы которых сами являются множествами. Например, множество a= состоит из двух элементов 2 и 1, а множество <a> , состоит из одного элемента a , который сам является двухэлементным множеством.
Два множества называюся равными, если они состоят из одних и тех же элементов. Например, равны множество равносторонних треугольников и множество равноугольных треугольников, так как это одни и те же треугольники: если в треугольнике все стороны равны, то равны и все его углы. Обратно, из равенства всех трёх углов треугольника вытекает равенство всех трёх его сторон. Равны любые два конечных множетсва, отличающиеся друг от друга только лишь порядком их элементов, например, <a, b, c> = <c, a, b> .
Пример 1. Равны ли множества
Решение. Так как множества и состоят из одних и тех же элементов, то они равны.
Множества и <> не равны, так как первое множество двухэлементное, а второе — одноэлементное.
Пример 2. Даны три множества:
Соотношение A∈B верно, так как множество A является первым элементом множества B.
Соотношение B∈C верно, так как множество B является первым элементом множества C.
Соотношение A∉C верно, так как множество A не является элементом множества C. Множество A является элементом множества B, которое является элементом множества C, но множества A и B — это разные множества.
Если А — конечное множество, то через 
Видео:Действия над множествамиСкачать

Подмножества
Всякий квадрат является прямоугольником. Из этого следует, что множество квадратов является частью множества прямоугольников, или, как говорят в математике, является подмножеством множества прямоугольников.
Множество А включено в множество В (символическая запись 
Если 


Например, если 

Верно следующее утверждение: пустое множество есть подмножество любого множества, то есть для любого множества А

Если множество содержит по крайней мере два элемента, то оно имеет всевозможные подмножества, среди которых есть и собственные подмножества.
Например, всевозможные подмножества множества 
из которых 


Множество всех подмножеств множества А называется множеством-степенью множества А и обозначается 
Например, если 
Теорема о мощности множества степени:
Если 

Упомянем пример практического применения этого понятия теории множеств — подмножества — в теории игр: с помощью подмножеств моделируется создание коалиций и проверяется, выгодно ли игрокам (в частности, в бизнесе) объединяться в коалиции для достижения общих целей.
Решить задачу на множества самостоятельно, а затем посмотреть решение
Пример 3. Сколько элементов содержит множество
Видео:9 класс, 2 урок, Множества и операции над нимиСкачать

Основные числовые множества
За подробным изложением, включающим также свойства операций над числами из различных множеств, можно обратиться к материалу Множества чисел. А на этой странице — краткий экскурс.
Числа, которые можно использовать для счёта предметов (то есть положительные целые числа, часто к ним относят и ноль) составляют множество натуральных чисел N :
Натуральные числа, числа противоположные им по знаку (то есть, отрицательные целые числа) и ноль составляют множество целых чисел Z :
Числа, записанные в виде p/q , причём p и q — целые числа и q не равно нулю, составляют множество рациональных чисел Q .
Например, 

Рациональные числа могут быть представлены в виде конечных либо бесконечных периодических дробей, например:
Числа 

Числа, которые можно представить в виде непериодических дробей, составляют множество иррациональных чисел I :
Рациональные и иррациональные числа составляют множество действительных чисел R :
Таким образом, имеют место следующие включения множеств:
Пример 4. Пусть A — множество всех натуральных чётных чисел больше нуля, а B — множество всех натуральных чисел, представимых в виде суммы двух нечётных натуральных чисел. Доказать, что A=B .
Решение. Для доказательства равенства данных множеств покажем, что каждый элемент множества A является элементом и множества B , и наоборот, каждый элемент множества B является и элементом множества A .
Шаг 1. Элемент принадлежит множеству A : x∈A . Докажем, что элемент x принадлежит и множеству B . Если x∈A , то x = 2k , где k ≥ 1 (любое число, умноженное на 2, является чётным числом). Но x = 2k можно представить и в виде (2k — 1) + 1 , что является суммой двух нечётных натуральных чисел. Натуральных, поскольку k ≥ 1 . Следовательно, x∈B .
Шаг 2. Элемент принадлежит множеству B : x∈B . Докажем, что элемент x принадлежит и множеству A . Если x∈B , то x = (2k — 1) + (2m — 1) , где 2k — 1 и 2m — 1 — нечётные натуральные числа, т.е. 2k — 1 ≥ 1 и 2m — 1 ≥ 1 . Следовательно, x = (2k + 2m — 2) = 2(k + m — 1) , где k + m — 1 ≥ 1 , значит, x∈A .
Таким образом, равенство множеств A и B доказано.
Устоявшиеся ныне представления о числовых множествах явились результатом эволюции изучения математиками различных чисел и добавления новых множеств (систем) чисел. Древнегреческие математики считали «настоящими» только натуральные числа, но в практических расчётах за два тысячелетия до н.э. в Древнем Египте и Древнем Вавилоне уже применялись дроби. Следующим важным этапом в развитии понятий о числе было введение отрицательных чисел — это было сделано китайскими математиками за два века до н.э. Отрицательные числа применял в III веке н.э. древнегреческий математик Диофант, знавший уже правила действий над ними. А в VII веке н.э. эти числа подробно изучили индийские математики, которые сравнивали такие числа с долгом. С помощью отрицательных чисел можно было единым образом описывать изменения величин. В результате всех этих занятий и сложилось близкое к современному понятие о множестве целых чисел, а в результате изучения свойств дробей — о множествах рациональных и иррациональных чисел.
После XVI века в связи с изучений квадратных и кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В начале такая постановка вопроса казалась парадоксом, но целый ряд таких задач был решён — так было заложено понятие множества комплексных чисел.
Видео:Свойства действий над множествамиСкачать

Операции над множествами: объединение, пересечение, разность, декартово произведение
Операция объединения множеств
Объединением множеств А и В называется множество, обозначаемое 

Например, если 





Операции над множествами удобно иллюстрировать фигурами, называемыми диаграммами Венна (другое название — круги Эйлера). На рисунке ниже слева большим и малым кругами обозначены соответственно множества А и В, а справа — результат объединения этих множеств (заштрихованная фигура).
Операция пересечения множеств
Пересечением множеств А и В называется множество, обозначаемое 

Например, если 





На рисунке ниже — результат пересечения множеств А и В — заштрихованная фигура.
Операция пересечения есть в реляционной алгебре, используемой для манипулирования данными в языках запросов к базам данных, например, SQL.
Разность множеств
Разностью множеств А и В называется множество, обозначаемое 

Например, если 







На рисунке ниже слева — результат разности множеств А и В, а справа — результат разности множеств В и А.
Операция разности есть в реляционной алгебре, используемой для манипулирования данными в языках запросов к базам данных, например, SQL.
Выполнить операции над множествами самостоятельно, а затем посмотреть решение
Пример 5. Выполните следующие операции над множествами:
Пример 6. Согласно опросу 100 покупателей рынка, купивших цитрусовые, апельсины купили 29 покупателей, лимоны — 30 покупателей, мандарины — 9, только мандарины — 1, апельсины и лимоны — 10, лимоны и мандарины — 4, все три вида фруктов — 3 покупателя. Сколько покупателей не купили ни одного вида перечисленных здесь цитрусовых? Сколько покупателей купили только лимоны?
Операция декартова произведения множеств
Для определения ещё одной важной операции над множествами — декартова произведения множеств введём понятие упорядоченного набора длины n.
Длиной набора называется число n его компонент. Набор, составленный из элементов 



Сейчас последует строгое определение, которое, возможно, не сразу понятно, но после этого определения будет картинка, по которой станет понятно, как получить декартово произведение множеств.
Декартовым (прямым) произведением множеств 


Например, если 




А теперь обещанная картинка
На картинке точками (узлами) дерева обозначены элементы множеств 


Операция декартова произведения есть в реляционной алгебре, используемой для манипулирования данными в языках запросов к базам данных, например, SQL.
Выполнить операции над множествами самостоятельно, а затем посмотреть решение
Пример 7. Даны множества:
Выполнить операции декартова произведения множеств:
Видео:Простейшие операции над множествамиСкачать

Свойства операций над множествами
Свойства используются для упрощения выражений. Они следующие.



Законы де Моргана:

Черта сверху означает отрицание.
Закон двойного отрицания:


Для следующего закона введём понятие универсума. Если допустить, что множество А является подмножеством некоторого фиксированного (поэтому на рисунке внизу оно ограничено сторонами квадрата) множества U, то множество U является универсальным (для данного случая) или универсумом. Например, в геометрии мы имеем дело с множествами точек данного пространства, в элементарной арифметике — с подмножествами множества всех целых чисел. Таким образом, множество всех целых чисел в данном случае можно считать универсальным множеством или универсумом.
Законы об универсуме и пустом множестве:





Видео:Операции над множествамиСкачать

Решение различных задач на множества
Пример 8. Найти декартово произведение множеств 


Решение. В качестве декартова произведения данных трёх множеств мы должны получить множество наборов длины 3 (по числу перемножаемых множеств). Смотрим на дерево для получения наборов (в теретической справке выше), проходим каждый полный маршрут от корня к конечным точкам и получаем:
Пример 9. Если 




Решение. Итак, множество А строго включено в множество В . Или, как на диаграмме Венна:
Объединение множеств 

или, что то же самое
но 
следовательно, если 

Пересечение множеств 


следовательно, если 

Разность множеств 

следовательно, если 

Разность множеств 


Следовательно, если 

Пример 10. Даны множества 



Решение. Найдём декартово произведение двух множеств. Можем так же пользоваться рисунком дерева из теоретической части, но в случае двух множеств маршрутов для составления упорядоченных наборов будет меньше. Получаем:
Для нахождения множества всех подмножеств полученное множество не совсем удобно: оно само состоит из двухэлементных множеств, в которых можно быстро запутаться. Поэтому выполним следующие присваивания:




Теперь будет проще найти множество всех подмножеств:
Очевидно, что 
Найдём 

Таким образом, 
Найдём 

Таким образом, 

Перемножаемые множества имеют равные размеры, но они не равны, так как состоят из разных элементов.
Пример 11. Упростить выражения.

Решение. Используя законы де Моргана, получаем:


Решение. Выражение во внутренних скобках уже упрощено в предыдущей части примера. Подставляем его и далее используя законы де Моргана, закон двойного отрицания и закон поглощения, получаем:


Решение. Упростим выражение в первых внутренних скобках, используя законы де Моргана и закон о двойном отрицании:
Из этого, используя законы об универсуме, пустом множестве и двойном отрицании, получаем:
Видео:Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебраСкачать

Треугольники, множества и алгебра
Иногда кажется, что некоторые математические темы изучены вдоль и поперек, например, треугольники. Ну что в этих треугольниках может быть нового и интересного? Тем не менее, даже такие, казалось бы, тривиальные объекты могут предстать под неожиданным углом. Давайте возьмем какую-нибудь простенькую задачку и попробуем ее решить. Постараемся найти треугольник с целочисленными сторонами, медианами и площадью. Мало ли, вдруг у нас получится.
Как перечислить все треугольники?
Даже несмотря на то, что некоторые множества содержат бесконечное количество элементов, они являются перечислимыми. Например, множество четных чисел может быть перечислено с помощью очень простого алгоритма — для любого n выдаем 2n и все. Во многом такая простота перечислимости некоторых множеств обусловлена тем, что элементы как-то упорядочены. Фактически, перечислить — значит пронумеровать, например, 2 — это первое четное число, 6 — третье. Но можем ли мы проделать то же самое с треугольниками? Если задавать треугольники с помощью кортежей вида a,b,c, то можем ли мы сказать, что треугольник 1,1,1 является первым, а треугольник 3,2,2 — четвертым или восьмым или еще каким-нибудь номером? Оказывается, можем.
Первое, что нужно придумать — это то как упорядочить множество треугольников. Первое, что приходит в голову — взять треугольник с какой-нибудь одной фиксированной стороной и выписать другие треугольники, стороны которого не меньше заданной. Например, так:
Как видим, первая сторона неизменна, а третья не превосходит суммы двух первых, на графике это будет выглядеть так:
Перед нами две ступенчатые функции, а значит мы можем задать стороны всех таких треугольников следующим образом:
Если заменить тройку на а
на
, то получим следующее:
Теперь любой треугольник можно изображать в виде точки на координатной плоскости, преобразуя стороны треугольников в координаты по двум простым формулам:
Чтобы перейти от координат к номерам достаточно воспользоваться канторовской нумерацией:
Или, если вместо координат использовать стороны треугольника:
Не знаю как вы, а я очень удивился, когда понял, что у каждого треугольника с целыми сторонами может быть свой номер. Есть что-то необычное в том, что подмножества треугольников, например, равнобедренные, могут выглядеть вот так:
Причем тут алгебра?
Очень похоже, что номера равнобедренных треугольников представляют собой множество парабол, нарисованных на одном графике. Так и есть, каждая из них может быть задана уравнением вида:
То же самое можно сказать и про многие другие подмножества треугольников. Например, вот так будут выглядеть треугольники с целыми, четными сторонами и одной целой медианой, проведенной к стороне :
На графике с координатами расположено множество кубических функций вида:
Не знаю, можно ли задать функции для всех кубических функций, но некоторые из них могут быть заданы, например, так:
Можно взять какую-то отдельную из них, например при j=0 и получить следующие формулы для координат треугольников:
Используя данные координаты можем задать функции для сторон и медианы:
Мы можем попробовать провернуть то же самое для треугольников, у которых две целые медианы:
Хоть этого и не видно на графике, но координаты треугольников с двумя целыми медианами задаются кубическими, квадратичными и линейными функциями. К сожалению, не могу привести все выкладки куда−то потерялись записи.
Если мы нарисуем график для треугольников с тремя целыми медианами, то получим следующее:
Таких треугольников очень мало, они очень сильно разрежены, но любопытно, что если найти хотя бы один такой треугольник, то все последующие могут быть заданы как:
Например, если взять треугольник 136, 170, 172 и умножить его стороны на 5, то мы снова получим треугольник с целыми сторонами и медианами.
Почему это все бесполезно?
Сначала кажется, что нумерация треугольников это шажок в сторону создания системы диофантовых уравнений, которые определяли бы стороны треугольников с целыми сторонами и медианами. Затем эти уравнения можно было бы подставить в формулу Герона и потом попытаться доказать возможность получения или неполучения треугольников с целой площадью. Но, к сожалению, нумерация треугольников абсолютно бесполезна в этом направлении. Все дело в том, что сама задача поиска треугольников с целыми сторонами и медианами связана с простыми числами. Сначала это кажется не совсем очевидным, но если следующее тождество является верным
то медиана не может быть целым числом. А это значит, что сама задача поиска треугольников с целыми сторонами и медианами наверняка может быть переведена на язык теории чисел, правда не знаю как.
В заключение
Сама идея того, что можно навести какой-никакой порядок в неупорядоченных множествах, очень любопытна. Например, можно попытаться каким-нибудь образом упорядочить матрицы из натуральных чисел, или графы определенного типа. Можно ли извлечь какую-то пользу от такого упорядочивания, это уже другой вопрос.
Видео:Множества. Операции над множествамиСкачать

Операции над множествами
Видео:Пересечение и объединение множеств. Алгебра, 8 классСкачать

Пересечение множеств
Рассмотрим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = < | Том, Фред, Макс, Джорж > |
| Друзья Майкла = < | Лео, Том, Фред, Эван > |
Видим, что Том и Фред одновременно являются друзьями Джона и Майкла.
Говоря на языке множеств, элементы Том и Фред принадлежат как множеству друзей Джона, так и множеству друзей Майкла.
Зададим новое множество с названием «Общие друзья Джона и Майкла» и в качестве элементов добавим в него Тома и Фреда :
| Общие друзья Джона и Майкла | = |
В данном случае множество «Общие друзья Джона и Майкла» является пересечением множеств друзей Джона и Майкла.
Пересечением двух (или нескольких) исходных множеств называется множество, которое состоит из элементов, принадлежащих каждому из исходных множеств.
В нашем случае элементы Том и Фред принадлежат каждому из исходных множеств, а именно: множеству друзей Джона и множеству друзей Майкла.
Обозначим множество друзей Джона через букву A , множество друзей Майкла — через букву B , а множество общих друзей Джона и Майкла обозначим через букву C :
Тогда пересечением множеств A и B будет множество C и записываться следующим образом:
Символ ∩ означает пересечение.
Говоря о множестве, обычно подразумевают элементы, принадлежащие этому множеству. Символ пересечения ∩ читается, как союз И. Тогда выражение A ∩ B = C можно прочитать следующим образом:
«Элементы, принадлежащие множеству A И множеству B, есть элементы, принадлежащие множеству C».
«Друзья, одновременно принадлежащие Джону И Майклу, есть общие друзья Джона и Майкла».
Теперь представим, что у Джона и Майкла нет общих друзей. Для удобства, как и прежде обозначим множество друзей Джона через букву A , а множество друзей Майкла через букву B
В этом случае говорят, что исходные множества не имеют общих элементов и пересечением таких множеств является пустое множество. Пустое множество обозначается символом ∅
Пример 2. Рассмотрим два множества: множество A , состоящее из чисел 1, 2, 3, 5, 7 и множество B, состоящее из чисел 1, 2, 3, 4, 6, 12, 18
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Множество С является пересечением множеств A и B , поскольку элементы множества C одновременно принадлежат множеству A и множеству B
Пример 3. Рассмотрим два множества: множество A, состоящее из чисел 1, 5, 7, 9 и множество B , состоящее из чисел 1, 4, 5, 7
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Множество С является пересечением множеств A и B , поскольку элементы множества C одновременно принадлежат множеству A и множеству B.
Пример 4. Найти пересечение следующих множеств:
Пересечением множеств A , B и C будет множество, состоящее из элементов, принадлежащих каждому из множеств A , B и C . Этими элементами являются числа 3 и 9.
Зададим новое множество D и добавим в него элементы 3 и 9. Затем с помощью символа пересечения ∩ запишем, что пересечением множеств A, B и C является множество D
Чтобы найти пересечение, вовсе необязательно задавать множества с помощью букв. Если элементов мало, то множество можно задать прямым перечислением элементов.
К примеру, пусть первое множество состоит из элементов 1, 3, 5, а второе из элементов 2, 3, 5 . Пересечением в данном случае является множество, состоящее из элементов 3 и 5 . Чтобы записать пересечение, можно воспользоваться прямым перечислением:
Числовые промежутки, которые мы рассмотрели в предыдущих уроках, тоже являются множествами. Элементами таких множеств являются числа, входящие в числовой промежуток.
Например, отрезок [2; 6] можно понимать, как множество всех чисел от 2 до 6. Для наглядности можно перечислить все целые числа, принадлежащие данному отрезку:
Следует иметь ввиду, что мы перечислили только целые числа. Отрезку [2; 6] также принадлежат и другие числа, не являющиеся целыми, например, десятичные дроби. Десятичные дроби располагаются между целыми числами, но их количество настолько велико, что перечислить их не представляется возможным.
Еще пример. Интервал (2; 6) можно понимать, как множество всех чисел от 2 до 6, кроме чисел 2 и 6. Ранее мы говорили, что интервал это такой числовой промежуток, границы которого не принадлежат ему. Для наглядности можно перечислить все целые числа, принадлежащие интервалу (2; 6) :
Поскольку числовые промежутки являются множествами, то мы можем находить пересечения между различными числовыми промежутками. Рассмотрим несколько примеров.
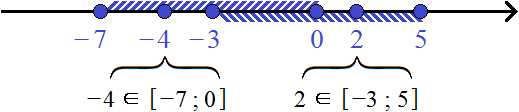
Пример 5. Даны два числовых промежутка: [2; 6] и [4; 8] . Найти их пересечение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [2; 6] и [4; 8] :
Видно, что числа 4, 5, 6 принадлежат как первому промежутку [2; 6] , так и второму [4; 8] .
Тогда пересечением числовых промежутков [2; 6] и [4; 8] будет числовой промежуток [4; 6]
Изобразим промежутки [2; 6] и [4; 8] на координатной прямой. На верхней области отметим числовой промежуток [2; 6] , на нижней — промежуток [4; 8]
Видно, что числа, принадлежащие промежутку [4; 6] , принадлежат как промежутку [2; 6] , так и промежутку [4; 8] . Можно также заметить, что штрихи, входящие в промежутки [2; 6] и [4; 8] пересекаются в промежутке [4; 6] . В такой ситуации, когда перед глазами есть координатная прямая, понятие пересечения множеств можно понимать в прямом смысле, что очень удобно.
Пример 6. Найти пересечение числовых промежутков [−2; 3] и [4; 7]
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [−2; 3] и [4; 7] :
−2, −1, 0, 1, 2, 3 ∈ [−2; 3]
Видно, что числовые промежутки [−2; 3] и [4; 7] не имеют общих чисел. Поэтому их пересечением будет пустое множество:
Если изобразить числовые промежутки [−2; 3] и [4; 7] на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Пример 7. Дано множество из одного элемента . Найти его пересечение с промежутком (−3; 4)
Множество, состоящее из одного элемента , на координатной прямой изображается в виде закрашенного кружка, а числовой промежуток (−3; 4) это интервал, границы которого не принадлежат ему. Значит границы −3 и 4 будут изображаться в виде пустых кружков:
Пересечением множества и числового промежутка (−3; 4) будет множество, состоящее из одного элемента , поскольку элемент 2 принадлежит как множеству , так и числовому промежутку (−3; 4)
На самом деле мы уже занимались пересечением числовых промежутков, когда решали системы линейных неравенств. Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.
По сути, множество решений, удовлетворяющих обоим неравенствам, является пересечением множеств решений первого и второго неравенства. Роль этих множеств берут на себя числовые промежутки.
Например, чтобы решить систему неравенств 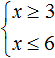
В данном примере решением первого неравенства x ≥ 3 является множество всех чисел, которые больше 3 (включая само число 3). Иначе говоря, решением неравенства является числовой промежуток [3; +∞)
Решением второго неравенства x ≤ 6 является множество всех чисел, которые меньше 6 (включая само число 6). Иначе говоря, решением неравенства является числовой промежуток (−∞; 6]
А общим решением системы будет пересечение множеств решений первого и второго неравенства, то есть пересечение числовых промежутков [3; +∞) и (−∞; 6]
Если мы изобразим множество решений системы 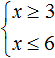
Поэтому в качестве ответа мы указывали, что значения переменной x принадлежат числовому промежутку [3; 6], то есть пересечению множеств решений первого и второго неравенства
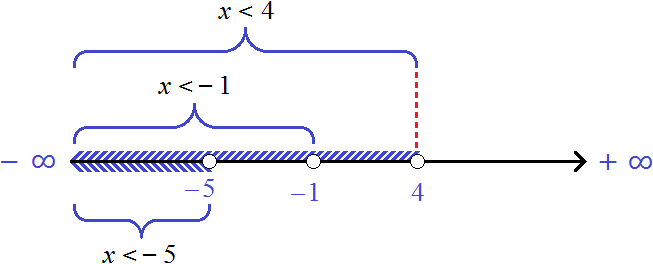
Пример 2. Решить неравенство
Все неравенства, входящие в систему уже решены. Нужно только указать те решения, которые являются общими для всех неравенств.
Решением первого неравенства является числовой промежуток (−∞; −1) .
Решением второго неравенства является числовой промежуток (−∞; −5) .
Решением третьего неравенства является числовой промежуток (−∞; 4) .
Решением системы 
На рисунке представлены числовые промежутки и неравенства, которыми эти числовые промежутки заданы. Видно, что числа, принадлежащие промежутку (−∞; −5) , одновременно принадлежат всем исходным промежуткам.
Запишем ответ к системе 
Пример 3. Решить неравенство
Решением первого неравенства y > 7 является числовой промежуток (7; +∞) .
Решением второго неравенства y является числовой промежуток (−∞; 4) .
Решением системы 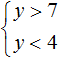
В данном случае пересечением числовых промежутков (7; +∞) и (−∞; 4) является пустое множество, поскольку эти числовые промежутки не имеют общих элементов:
Если изобразить числовые промежутки (7; +∞) и (−∞; 4) на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Видео:Множество. Элементы множества. 5 класс.Скачать

Объединение множеств
Объединением двух (или нескольких) исходных множеств называют множество, которое состоит из элементов, принадлежащих хотя бы одному из исходных множеств.
На практике объединение множеств состоит из всех элементов, принадлежащих исходным множествам. Поэтому и говорят, что элементы такого множества принадлежат хотя бы одному из исходных множеств.
Рассмотрим множество A с элементами 1, 2, 3 и множество B с элементами 4, 5, 6.
Зададим новое множество C и добавим в него все элементы множества A и все элементы множества B
В данном случае объединением множеств A и B является множество C и обозначается следующим образом:
Символ ∪ означает объединение и заменяет собой союз ИЛИ. Тогда выражение A ∪ B = C можно прочитать так:
Элементы, принадлежащие множеству A ИЛИ множеству B, есть элементы, принадлежащие множеству C.
В определении объединения сказано, что элементы такого множества принадлежат хотя бы одному из исходных множеств. Данную фразу можно понимать в прямом смысле.
Вернёмся к созданному нами множеству C , куда входят все элементы множеств A и B . Возьмём для примера из этого множества элемент 5. Что можно про него сказать?
Если 5 является элементом множества C , а множество С является объединением множеств A и B , то можно с уверенностью заявить, что элемент 5 принадлежит хотя бы одному из множеств A и B . Так оно и есть:
Возьмем ещё один элемент из множества С , например, элемент 2. Что можно про него сказать?
Если 2 является элементом множества C , а множество С является объединением множеств A и B , то можно с уверенностью заявить, что элемент 2 принадлежит хотя бы одному из множеств A и B . Так оно и есть:
Если мы захотим объединить два или более множества и вдруг обнаружим, что один или несколько элементов принадлежат каждому из этих множеств, то в объединение повторяющиеся элементы будут входить только один раз.
Например, рассмотрим множество A с элементами 1, 2, 3, 4 и множество B с элементами 2, 4, 5, 6.
Видим, что элементы 2 и 4 одновременно принадлежат и множеству A , и множеству B . Если мы захотим объединить множества A и B , то новое множество C будет содержать элементы 2 и 4 только один раз. Выглядеть это будет так:
Чтобы при объединении не допустить ошибок, обычно поступают так: сначала в новое множество добавляют все элементы первого множества, затем добавляют элементы второго множества, которые не принадлежат первому множеству. Попробуем сделать такое объединение с множествами A и B .
Итак, у нас имеются следующие исходные множества:
Зададим новое множество С и добавим в него все элементы множества A
Теперь добавим элементы из множества B , которые не принадлежат множеству A . Множеству A не принадлежат элементы 5 и 6 . Их и добавим во множество C
Пример 2. Друзьями Джона являются Том, Фред, Макс и Джордж. А друзьями Майкла являются Лео, Том, Фред и Эван. Найти объединение множеств друзей Джона и Майкла.
Для начала зададим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = < | Том, Фред, Макс, Джорж > |
| Друзья Майкла = < | Лео, Том, Фред, Эван > |
Зададим новое множество с названием «Все друзья Джона и Майкла» и добавим в него всех друзей Джона и Майкла.
Заметим, что Том и Фред одновременно являются друзьями Джона и Майкла, поэтому мы добавим их в новое множество только один раз, поскольку сразу двух Томов и двух Фредов не бывает.
| Все друзья Джона и Майкла | = |
В данном случае множество всех друзей Джона и Майкла является объединением множеств друзей Джона и Майкла.
Друзья Джона ∪ Друзья Майкла = Все друзья Джона и Майкла
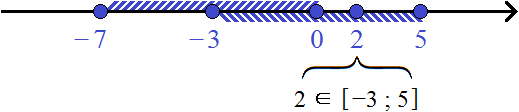
Пример 3. Даны два числовых промежутка: [−7; 0] и [−3; 5] . Найти их объединение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие этим промежуткам:
−7, −6, −5, −4, −3,−2, −1 , 0 ∈ [−7; 0]
−3,−2, −1 , 0, 1, 2, 3, 4, 5 ∈ [−3; 5]
Объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5] , который содержит все числа промежутка [−7; 0] и [−3; 5] без повторов некоторых из чисел
−7, −6, −5, −4, −3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−7; 5]
Обратите внимание, что числа −3,−2, −1 принадлежали и первому промежутку и второму. Но поскольку в объединение допускается включать такие элементы только один раз, мы включили их единоразово.
Значит объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5]
Изобразим на координатной прямой промежутки [−7; 0] и [−3; 5] . На верхней области отметим числовой промежуток [−7; 0] , на нижней — промежуток [−3; 5]
Ранее мы выяснили, что промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5] . Здесь полезно вспомнить про определение объединения множеств, которое было приведено в самом начале. Объединение трактуется, как множество, состоящее из всех элементов, принадлежащих хотя бы одному из исходных множеств.
Действительно, если взять любое число из промежутка [−7; 5] , то окажется, что оно принадлежит хотя бы одному из промежутков: либо промежутку [−7; 0] либо промежутку [−3; 5] .
Возьмём из промежутка [−7; 5] любое число, например число 2 . Поскольку промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5] , то число 2 будет принадлежать хотя бы одному из этих промежутков. В данном случае число 2 принадлежит промежутку [−3; 5]
Возьмём ещё какое-нибудь число. Например, число −4 . Это число будет принадлежать хотя бы одному из промежутков: [−7; 0] или [−3; 5] . В данном случае оно принадлежит промежутку [−7; 0]
Возьмём ещё какое-нибудь число. Например, число −2 . Оно принадлежит как промежутку [−7; 0] , так и промежутку [−3; 5] . Но на координатной прямой оно указывается только один раз, поскольку в одной точке сразу два числа −2 не бывает.
Не каждое объединение числовых промежутков является числовым промежутком. Например, попробуем найти объединение числовых промежутков [−2 ; −1] и [4 ; 7].
Идея остаётся та же самая — объединением числовых промежутков [−2 ;−1] и [4 ; 7] будет множество, состоящее из элементов, принадлежащих хотя бы одному из промежутков: [−2; −1] или [4; 7] . Но это множество не будет являться числовым промежутком. Для наглядности перечислим все целые числа, принадлежащие этому объединению:
Получили множество . Это множество не является числовым промежутком по причине того, что числа, располагающиеся между −1 и 4 , не вошли в полученное множество
Числовой промежуток должен содержать все числа от левой границы до правой. Если одно из чисел отсутствует, то числовой промежуток теряет смысл. Допустим, имеется линейка длиной 15 см
Эта линейка является числовым промежутком [0; 15], поскольку содержит все числа в промежутке от 0 до 15 включительно. Теперь представим, что на линейке после числа 9 сразу следует число 12.
Эта линейка не является линейкой в 15 см, и её нежелательно использовать для измерения. Также, её нельзя назвать числовым промежутком [0; 15] , поскольку она не содержит все числа, которые должна была содержать.
Видео:Множества и операции над множествамиСкачать

Решение неравенств, содержащих знак ≠
Некоторые неравенства содержат знак ≠ (не равно). Например, 2x ≠ 8 . Чтобы решить такое неравенство, нужно найти множество значений переменной x , при которых левая часть не равна правой части.
Решим неравенство 2x ≠ 8 . Разделим обе части данного неравенства на 2, тогда получим:
Получили равносильное неравенство x ≠ 4 . Решением этого неравенства является множество всех чисел, не равных 4. То есть если мы подставим в неравенство x ≠ 4 любое число, которое не равно 4, то получим верное неравенство.
Подставим, например, число 5
5 ≠ 4 — верное неравенство, поскольку 5 не равно 4
7 ≠ 4 — верное неравенство, поскольку 7 не равно 4
И поскольку неравенство x ≠ 4 равносильно исходному неравенству 2x ≠ 8 , то решения неравенства x ≠ 4 будут подходить и к неравенству 2x ≠ 8 . Подставим те же тестовые значения 5 и 7 в неравенство 2x ≠ 8 .
Изобразим множество решений неравенства x ≠ 4 на координатной прямой. Для этого выколем точку 4 на координатной прямой, а всю оставшуюся область с обеих сторон выделим штрихами:
Теперь запишем ответ в виде числового промежутка. Для этого воспользуемся объединением множеств. Любое число, являющееся решением неравенства 2x ≠ 8 будет принадлежать либо промежутку (−∞; 4) либо промежутку (4; +∞). Так и записываем, что значения переменной x принадлежат (−∞; 4) или (4; +∞) . Напомним, что для слова «или» используется символ ∪
В этом выражении говорится, что значения, принимаемые переменной x , принадлежат промежутку (−∞; 4) или промежутку (4; +∞).
Неравенства, содержащие знак ≠ , также можно решать, как обычные уравнения. Для этого знак ≠ заменяют на знак = . Тогда получится обычное уравнение. В конце решения найденное значение переменной x нужно исключить из множества решений.
Решим предыдущее неравенство 2x ≠ 8 , как обычное уравнение. Заменим знак ≠ на знак равенства = , получим уравнение 2x = 8 . Разделим обе части данного уравнения на 2 , получим x = 4 .
Видим, что при x , равном 4, уравнение обращается в верное числовое равенство. При других значениях равенства соблюдаться не будет. Эти другие значения нас и интересуют. А для этого достаточно исключить найденную четвёрку из множества решений.
Пример 2. Решить неравенство 3x − 5 ≠ 1 − 2x
Перенесем −2x из правой части в левую часть, изменив знак, а −5 из левой части перенесём в правую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 5
Решением неравенства x ≠ 1,2 является множество всех чисел, не равных 1,2 .
Изобразим множество решений неравенства x ≠ 1,2 на координатной прямой и запишем ответ в виде числового промежутка:
В этом выражении говорится, что значения, принимаемые переменной x принадлежат промежутку (−∞; 1,2) или промежутку (1,2; +∞)
Видео:Пересечение множеств. Объединение множеств. 5 класс.Скачать

Решение совокупностей неравенств
Рассмотрим ещё один вид неравенств, который называется совокупностью неравенств. Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их.
Совокупность неравенств очень похожа на систему неравенств. Различие в том, что в системе неравенств нужно найти множество решений, удовлетворяющих каждому неравенству, образующему эту систему.
А в случае с совокупностью неравенств, нужно найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность.
Совокупность неравенств обозначается квадратной скобкой. Например, следующая запись из двух неравенств является совокупностью:
Решим данную совокупность. Сначала нужно решить каждое неравенство по отдельности.
Решением первого неравенства x ≥ 3 является числовой промежуток [3; +∞) . Решением второго неравенства x ≤ 6 является числовой промежуток (−∞; 6] .
Множество значений x , при которых верно хотя бы одно из неравенств, будет принадлежать промежутку [3; +∞) или промежутку (−∞; 6] . Так и записываем:
В этом выражении говорится, что переменная x , входящая в
совокупность 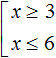
Например, число 9 из промежутка [3; +∞) удовлетворяет первому неравенству x ≥ 3. А число −7 из промежутка (−∞; 6] удовлетворяет второму неравенству x ≤ 6.
Посмотрите внимательно на выражение x ∈ [3; +∞) ∪ (−∞; 6], а именно на его правую часть. Ведь выражение [3; +∞) ∪ (−∞; 6] представляет собой объединение числовых промежутков [3; +∞) и (−∞; 6] . Точнее, объединение множеств решений первого и второго неравенства.
Стало быть, решением совокупности неравенств является объединение множеств решений первого и второго неравенства.
Иначе говоря, решением совокупности 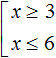
Объединением числовых промежутков [3; +∞) и (−∞; 6] является промежуток (−∞; +∞) . Точнее, объединением числовых промежутков [3; +∞) и (−∞; 6] является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
Возьмём любое число из полученного объединения, и проверим удовлетворяет ли оно хотя бы одному неравенству.
Возьмем для примера число 8. Оно удовлетворяет первому неравенству x ≥ 3.
Возьмем еще какое-нибудь число, например, число 1. Оно удовлетворяет второму неравенству x ≤ 6
Возьмем еще какое-нибудь число, например, число 5 . Оно удовлетворяет и первому неравенству x ≥ 3 и второму x ≤ 6
Пример 2. Решить совокупность неравенств
Чтобы решить эту совокупность, нужно найти множество решений, которые удовлетворяют хотя бы одному неравенству, образующему эту совокупность.
Для начала найдём множество решений первого неравенства x . Этим множеством является числовой промежуток (−∞; −0,25) .
Множеством решений второго неравенства x ≥ −7 является числовой промежуток [−7; +∞).
Решением совокупности неравенств 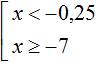
Иначе говоря, решением совокупности 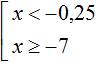
Объединением числовых промежутков (−∞; −0,25) и [−7; +∞) является является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
Пример 3. Решить совокупность неравенств
Решим каждое неравенство по отдельности:
Множеством решений первого неравенства x является числовой промежуток (−∞; −3) .
Множеством решений второго неравенства x ≤ 0 является числовой промежуток (−∞; 0] .
Решением совокупности неравенств 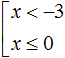
Иначе говоря, решением совокупности 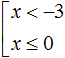
Объединением числовых промежутков (−∞; −3) и (−∞; 0] является числовой промежуток (−∞; 0]
Ответ можно оставить таким, каким мы его записали ранее:
🎥 Видео
УРОК 06. Операции над множествами (7 класс)Скачать

Операции над множествами (лучшее учебное видео!)Скачать
4. Множества. Операции над множествами. Дискретная математикаСкачать

ПОДМНОЖЕСТВА. Операции над множества. §14 алгебра 8 классСкачать

Множества — Принципы математического мышления — уровень 5 из 5Скачать

Операции над множествамиСкачать