Делит ли биссектриса треугольника пополам

Свойство точек биссектрисы угла:

По определению биссектриса угла делит угол пополам.

У биссектрисы есть еще одно важное свойство.

Теорема (о биссектрисе угла).

Любая точка биссектрисы угла равноудалена от сторон угла. Если точка внутри угла равноудалена от сторон угла, то она лежит на биссектрисе этого угла.

В данной теореме два утверждения: прямое и ему обратное. Докажем каждое из этих утверждений отдельно.

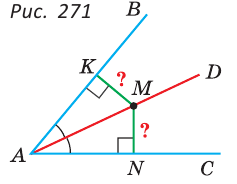
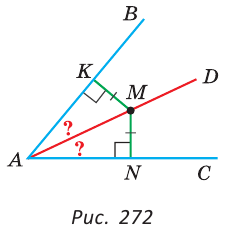
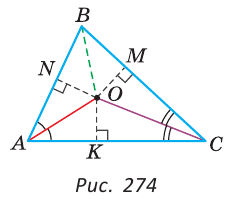
1) Дано: AD — биссектриса

Доказательство:

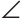
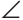
Прямоугольные треугольники АКМ и ANM равны по гипотенузе и острому углу (гипотенуза AM — общая, KAM =NAM, так как AD — биссектриса). Катеты МК и MN равны как соответствующие в двух равных треугольниках.

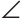
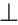
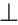
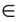
2) Дано: BAC, МКAB, MNAC, МК = MN, MAD (рис. 272).

Доказать: луч AD — биссектриса 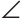BAC.

Доказательство:

Прямоугольные треугольники АКМ и ANM равны по катету и гипотенузе (гипотенуза AM — общая, МК = MN по условию). Углы КAM и NAM равны как соответствующие в двух равных треугольниках, откуда луч AD — биссектриса 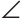BAC. Теорема доказана.

Из доказанной теоремы следует, что биссектриса является геометрическим местом точек плоскости, находящихся внутри угла и равноудаленных от сторон угла.

Пример:

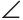
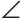
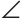
В прямоугольном треугольнике ABC C = 90°, A = 40° (рис. 273). На катете АС взята точка К так, что КС=6 см и KBC = 25°. Найти расстояние от точки К до прямой АВ.

Решение:

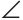
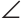
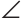
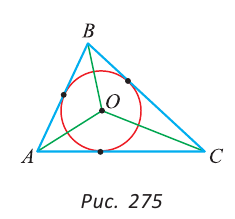
Искомое расстояние равно длине перпендикуляра КМ к прямой АВ. Так как ABC = 90° —A = 90° — 40° = 50°, то ABK = 50° — 25° = 25°. Следовательно, ВК — биссектриса угла ABC. Поскольку любая точка биссектрисы угла равноудалена от сторон угла, то КМ = КС = 6 см.

Пример: (2-я замечательная точка треугольника).

Доказать, что биссектрисы треугольника пересекаются в одной точке.

Доказательство:

Проведем в АВС биссектрисы углов А и С. Пусть О — точка их пересечения (рис. 274).

Так как точка О лежит на биссектрисе АО угла А, то она равноудалена от сторон угла А, то есть равны перпендикуляры ON и ОК к сторонам угла А. Так как точка О лежит на биссектрисе СО угла С, она равноудалена от сторон угла С, то есть равны перпендикуляры ОК и ОМ к сторонам угла С. Тогда ОК = ОМ = ON. Так как перпендикуляры ON и ОМ равны, то точка О равноудалена от сторон угла В. Точка, равноудаленная от сторон угла, лежит на биссектрисе этого угла. Поэтому биссектриса угла В пройдет через точку О, и, следовательно, все три биссектрисы пересекутся в одной точке.

Замечание. Точка пересечения биссектрис треугольника является центром вписанной в него окружности (рис. 275), которая касается всех трех сторон треугольника (имеет с каждой из сторон только одну общую точку).

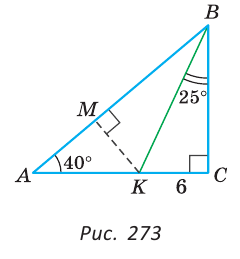
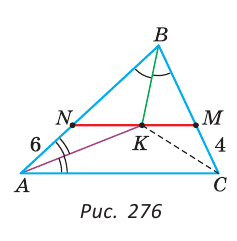
Пример:

В треугольнике ABC биссектрисы углов А и В пересекаются в точке К. Через точку К проведен отрезок NM, параллельный стороне АС с концами на сторонах АВ и ВС соответственно; AN = 6 см, МС = 4 см. Найти отрезок NM.

Решение:

Так как биссектрисы треугольника пересекаются в одной точке, то СК — биссектриса угла С (рис. 276).

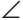
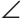
Треугольник ANK — равнобедренный. Действительно, NAK =CAK, поскольку АК — биссектриса, CAK =AKN как накрест лежащие при параллельных прямых NM и АС и секущей АК, откуда NAK =AKN и треугольник ANК — равнобедренный по признаку равнобедренного треугольника. Тогда NK=AN=6 см. Аналогично доказываем, что треугольник KMC — равнобедренный и КМ=МС=4 см.

Искомый отрезок NM = NK + КМ = 6 + 4=10 (см).

Замечание. Решив задачу 3, мы доказали, что если NM || АС и отрезок NM проходит через точку пересечения биссектрис, то периметр NBM равен АВ+ВС.

• Свойство катета прямоугольного треугольника, лежащего против угла в 30°
• Четырехугольник и его элементы
• Четырехугольники и окружность
• Параллелограмм, его свойства и признаки
• Признаки равенства прямоугольных треугольников
• Соотношения в прямоугольном треугольнике
• Сумма углов треугольника
• Внешний угол треугольника

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Элементы треугольника. Биссектриса

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

Видео:Биссектриса треугольника делит пополам сторону ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Видео:3 свойства биссектрисы #shortsСкачать

Некоторые формулы, связанные с биссектрисой треугольника

(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1

Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Видео:Построение биссектрисы угла. 7 класс.Скачать

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

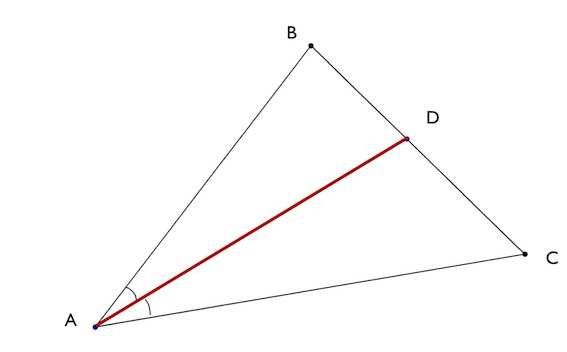
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Видео:№535. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки,Скачать

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

• CD – внутренняя биссектриса ∠ACB;
• CE – биссектриса угла, смежного с ∠ACB;
• ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Видео:Запоминаем: высота, медиана биссектриса треугольникаСкачать

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

📺 Видео

Биссектриса прямого угла делит медиану пополам! Найти площадь треугольника.Скачать

Геометрия В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину ВСкачать

Медиана треугольника делит пополам угол ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

ПОСТРОЕНИЕ БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Биссектрисы треугольника.Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Биссектриса угла. Геометрия 7 класс.Скачать

№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать

Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать

Свойства биссектрисы треугольникаСкачать

Геометрия Докажите что биссектриса треугольника делит его сторону на отрезки длины которых обратноСкачать

Формула для биссектрисы треугольникаСкачать

Биссектриса треугольника. Построение. 1 частьСкачать