Даны две стороны треугольника

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

.

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

.

Видео:Найдите третью сторону треугольникаСкачать

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Видео:Уравнения стороны треугольника и медианыСкачать

Даны две стороны треугольника ANK и высота NL, проведённая к стороне AK.

Даны следующие возможные шаги построения треугольника:

1. провести прямую.

3. Провести отрезок.

4. Провести окружность с данным центром и радиусом.

5. На данном луче от его начала отложить отрезок, равный данному.
6. Построить угол, равный данному.
7. Построить биссектрису угла.
8. Построить перпендикулярную прямую.
9. Построить середину отрезка.

1. Напиши, в каком порядке следует выполнить данные шаги в этом задании

(один и тот же шаг может повторяться, номер шага запиши без точки):

Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Две стороны и угол треугольника

Видео:Теорема косинусов. Две стороны треугольника равны 4 см и 8 см, а угол ....Скачать

Свойства

Зная две стороны в треугольнике и угол между ними, можно с помощью теоремы косинусов вычислить третью сторону треугольника. Для этого нужно извлечь квадратный корень из суммы квадратов известных сторон и разности с их удвоенным произведением на косинус угла между ними. (рис.76) a^2=b^2+c^2-2bc cos⁡α a=√(b^2+c^2-2bc cos⁡α )

Угол β или γ можно рассчитать через ту же теорему косинусов, зная две, образующие их стороны, при этом один из них – последний, проще найти, отняв два известных от 180 градусов. cos⁡β=(a^2+c^2-b^2)/2ac=(b^2+c^2-2bc cos⁡α+c^2-b^2)/(2c√(b^2+c^2-2bc cos⁡α ))=(2c^2-2bc cos⁡α)/(2c√(b^2+c^2-2bc cos⁡α ))=(c-b cos⁡α)/√(b^2+c^2-2bc cos⁡α ) cos⁡γ=(a^2+b^2-c^2)/2ab=(b^2+c^2-2bc cos⁡α+b^2-c^2)/(2b√(b^2+c^2-2bc cos⁡α ))=(b-c cos⁡α)/√(b^2+c^2-2bc cos⁡α )

Медиана треугольника рассчитывается по вполне однозначной формуле, тогда как если нужно найти медианы через две стороны и угол между ними, то требуются преобразования. m_a=√(2b^2+2c^2-a^2 )/2=√(2b^2+2c^2-b^2-c^2+2bc cos⁡α )/2=√(b^2+c^2+2bc cos⁡α )/2 m_b=√(2a^2+2c^2-b^2 )/2=√(2b^2+2c^2-4bc cos⁡α+2c^2-b^2 )/2=√(b^2+4c^2-4bc cos⁡α )/2 m_c=√(2a^2+2b^2-c^2 )/2=√(2b^2+2c^2-4bc cos⁡α+2b^2-c^2 )/2=√(4b^2+c^2-4bc cos⁡α )/2

Для расчета биссектрис в произвольном треугольнике также существуют стандартные формулы, из которых только одна может быть преобразована и упрощена для двух сторон и угла между ними. l_c=√(ab(a+b+c)(a+b-c))/(a+b) l_b=√(ac(a+b+c)(a+c-b))/(a+c) l_a=√(bc(a+b+c)(b+c-a))/(b+c)=√(bc((b-c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-b^2-c^2+2bc cos⁡α ) )/(b+c)=(bc√(2(1+cos⁡α ) ))/(b+c)

Чтобы найти высоту, нужно знать все три стороны в треугольнике. Подставив их в формулу так, чтобы сторона, на которую опущена искомая высота была в знаменателе, рассчитываются их величины. h_a=(2√(p(p-a)(p-b)(p-c) ))/a h_b=(2√(p(p-a)(p-b)(p-c) ))/b h_c=(2√(p(p-a)(p-b)(p-c) ))/c

Вычислить среднюю линию треугольника можно, зная лишь ту сторону, которой она параллельна, так как сторона будет в два раза больше. В случае с неизвестной стороной, можно подставить в формулу радикал,выведенный по теореме косинусов. M_a=a/2=√(b^2+c^2-2bc cos⁡α )/2 M_b=b/2 M_c=c/2

На пересечении биссектрис в треугольнике расположен центр окружности, которую можно в него вписать. Радиус такой окружности рассчитывается по следующей формуле(рис.75.5) r=√(((p-a)(p-b)(p-c))/p)

Центр описанной вокруг треугольника окружности в свою очередь расположен в точке пересечения медиатрисс, и его формула значительно видоизменена в сравнении с радиусом вписанной окружности. (рис.75.6) R=abc/(4√(p(p-a)(p-b)(p-c)))

📸 Видео

№52. Две стороны треугольника параллельны плоскости α. Докажите, что и третья сторонаСкачать

Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

Найдите сторону треугольника на рисункеСкачать

Две стороны треугольникаСкачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Геометрия Две стороны треугольника равны 12 см и 14 см а медиана проведенная к третьей стороне 7 смСкачать

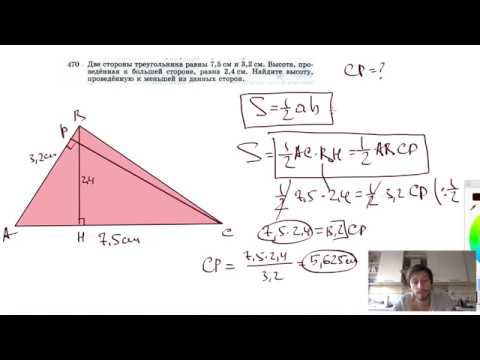
№470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведенная кСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Нахождение стороны прямоугольного треугольникаСкачать

Геометрия Две стороны треугольника относятся как 1:2√3 и образуют угол равный 30 Третья сторонаСкачать

ГОВОРЯТ, ОТВЕТ "8" НЕ НАСТОЯЩИЙ! Ограничения: 16+.Скачать

Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Решить за 45 минут Классная задача на построениеСкачать

Геометрия Две стороны треугольника угол между которыми равен 120 относятся как 5:3 Найдите стороныСкачать