Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Ваш ответ
Видео:Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

решение вопроса
Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,049
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:9 класс, 15 урок, Решение треугольниковСкачать

Два угла и сторона треугольника C
Видео:ЕГЭ Математика Задание 6#47363Скачать

Свойства
Для того чтобы рассчитать в треугольнике все возможные показатели, необходимо, как минимум, иметь данные о его сторонах. Зная два угла и сторону а, можно найти остальные две стороны и угол, построив высоту в таком треугольнике. (рис. 76.1) Высота разделит произвольный треугольник на два прямоугольных, в которых катетами будет высота и часть известной стороны x или y, а гипотенузами – неизвестные стороны a и b. Кроме того, что мы задаем известную сторону a, как сумму двух катетов x и y, тригонометрия полученных треугольников, определяет высоту с одной стороны как произведение y на тангенс β, а с другой стороны как произведение x на тангенс γ. Приравнивая эти выражения друг к другу, можно составить систему уравнений, из которых могут быть найдены части x и y, а затем неизвестные стороны первоначального треугольника a и b. <█(x+y=a@y tanβ=x tanγ )┤<█(x=a-y@y(tanβ+tanγ )=a tanγ )┤<█(x=a-y@y=(a tanγ)/(tanβ+tanγ ))┤ b=x/cosγ , c=y/cosβ h_a=y tanβ
Можно также найти сразу две другие высоты треугольника, опущенные на стороны b и c соответственно. (рис. 76.2) h_b=a sinβ h_c=a sinγ
Третий угол можно найти, зная, что сумма всех углов в треугольнике равна 180 градусам. α=180°-β-γ
Теперь, зная все стороны, углы и высоты, можно найти все остальные параметры треугольника. Вычислить периметр можно, сложив все три стороны, а площадь – умножив половину любой стороны на опущенную на нее высоту. P=a+b+c S=(ah_a)/2
Если провести в треугольнике медианы, то каждая из них разделит сторону, на которую она опущена, на две равные части. Для того, чтобы вычислить медиану в треугольнике, необходимо знать все три стороны. Формула медианы заключается в том, чтобы сложить удвоенные квадраты двух нетронутых сторон, отнять квадрат стороны, на которую опущена медиана, извлечь из этого выражения квадратный корень и разделить его на два. (рис. 75.1) m_c=√(2a^2+2b^2-c^2 )/2 m_a=√(2b^2+2c^2-a^2 )/2 m_b=√(2a^2+2c^2-b^2 )/2
Чтобы найти биссектрисы треугольника, которые делят пополам его углы, также необходимо знать все три стороны треугольника. Формула биссектрисы выглядит немного сложнее, чем формула медианы, но достаточно проста в расчетах. (рис.75.2) l_c=√(ab(a+b+c)(a+b-c))/(a+b) l_b=√(ac(a+b+c)(a+c-b))/(a+c) l_a=√(bc(a+b+c)(b+c-a))/(b+c)
Средняя линия треугольника – это прямая, проведенная параллельно одной из его сторон. Ее особенность заключается в том, что она делит стороны на которые опирается на две равные части, и сама равна половине стороны, ей параллельной. (рис.75.7) M_a=a/2 M_b=b/2 M_c=c/2
Также в произвольном треугольнике через стороны можно найти радиус окружности, которую можно вписать в треугольник или описать около него. Радиус вписанной окружности будет начинаться в точке пересечения биссектрис треугольника и опускаться на любую из сторон под прямым углом. Радиус описанной окружности начинается в точке пересечения медиатрисс треугольника и заканчивается в любой из его вершин. (рис. 75.5, 75.6) r=√(((p-a)(p-b)(p-c))/p) R=abc/(4√(p(p-a)(p-b)(p-c)))
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Решение косоугольных треугольников
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Решение треугольника по двум его углам и стороне
Задача. Даны два угла треугольника и сторона, прилежащая к ним; вычислить другие стороны и угол.
Даны В, С и а; требуется найти b, с и А.
Решение. Условие возможности построения треугольника по этим данным:
А + В 1 /0,9483 ≈ 1,055.
Вычисления выполнены по правилам приближённых вычислений. Значения синусов взяты из таблиц Брадиса; во всех промежуточных результатах сохраняются четыре значащие цифры (правило запасной цифры), а окончательный результат округлён до трёх значащих цифр.
Решение при помощи логарифмических таблиц. Имеем:
b = a sin B /sin A, lg b = lg a + lg sin В — lg sin A.
По таблицам найдем:
lg a = 1,2405, lg sinB = 1,8457, ld sin A = 1,9770, откуда lg b = 1,1092
По таблицам Брадиса найдём b = 12,86. Однако в ответе следует оставить три значащие цифры, так как значение а дано с тремя значащими цифрами; поэтому b ≈ 12,9.
Сторона с вычисляется аналогично:
c = a sin C /sin A, lg c = lg a + lg sin C — lg sin A.
. lg c = 1,2172; c ≈ 16,5
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Решение треугольника по двум сторонам и углу между ними
Задача. Даны две стороны треугольника и угол между ними; вычислить третью сторону и два других угла.
Пусть, например, даны а, b и С, требуется вычислить А, В и с.
Решение при помощи натуральных таблиц. Формула косинусов даёт выражение стороны с непосредственно через известные элементы:
Для вычисления А можно также воспользоваться формулой косинусов:
Разность углов A — В можно вычислить, воспользовавшись теоремой тангенсов:
Углы А и В определяются из системы уравнений:
Сторону с можно вычислить по теореме синусов:
Пример. Дано: а ≈ 49,4; b ≈ 26,4; С ≈ 47°20 найти А, В и с.
Решение при помощи натуральных таблиц. Имеем:
с 2 = а 2 + b 2 — 2ab cos С ≈ 49,4 2 + 26,4 2 — 2 • 49,4 • 26,4 • cos 47°20’
По таблицам квадратов найдём:
а 2 ≈ (49,4) 2 ≈ 2449; b 2 ≈ (26,4) 2 ≈ 697,0
2 • 49,4 • 26,4 • cos 47°20’ ≈ 2 • 49,4 • 2,64 • 0,6778 ≈ 1768.
Следовательно, с 2 ≈ 2440 + 697 — 1768 ≈ 1369. По таблицам квадратных корней
А ≈ arc cos (-0,191); угол А — тупой.
Находим дополнительный угол
180° — А ≈ arc cos (0,091) ≈ 79°; А ≈ 180° — 79° = 101°
(с округлением до 10’). Наконец,
Решение при помощи логарифмических таблиц. Вычислим углы A и В.
$$ lg tgfrac=lg(a-b) + lg ctgfrac — lg(a+b) $$
$$ lg tgfrac=1,8403 ;;и;; fracapprox 34°40’ $$
Из системы уравнений
найдём: A ≈ 101°, В ≈ 31°40’.
Видео:№1048. Найдите косинусы углов треугольника с вершинами А (2; 8),Скачать

Решение треугольника по двум сторонам и углу, противолежащему одной из них
Задача. Даны две стороны треугольника и угол А, лежащей против одной из них; вычислить третью сторону и два остальных угла.
Пусть даны a, b и А; требуется вычислить B, С и с
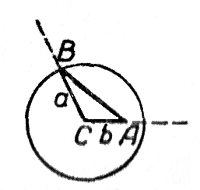
С л у ч а й 1. а > b, т. е, заданный угол А лежит против большей стороны.
Построение показано на чертеже. Из точки С (как из центра), взятой на одной из сторон угла А на расстоянии b от вершины, описана окружность радиуса а; точка В есть точка пересечения этой окружности с другой стороной угла А.
Построение всегда возможно, задача имеет единственное решение.
Острый угол В, противолежащий меньшей стороне, находится по теореме синусов:
и затем С = 180° — (A + В). Сторона с находится по теореме синусов: ( c=frac )
С л у ч а й 2. а 90° задача не имеет решения.
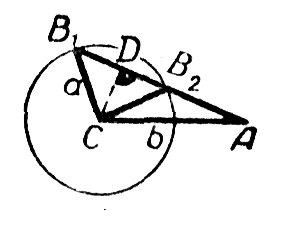
Пусть угол А острый. Из построения на чертеже a), видно, что окружность радиуса а с центром в точке С пересечёт другую сторону угла А в двух точках при условии а > CD, где D — основание перпендикуляра, опущенного из точки С на другую сторону угла A. Так как CD = b sinA (из треугольника ACD), то условие запишется так: a >b sinA.
Для угла В возможны два значения: В = В1 (острый) и В = В2 (тупой). Задача имеет два решения.
a) Значения угла В вычисляются по теореме синусов: ( sinB = fracsinA )
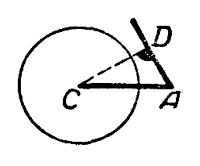
Из чертежа видно, что при CD = b sinА > а окружность не пересечёт другой стороны угла А; задача не имеет решений.
При CD = b sin А задача имеет единственное решение: треугольник ABC прямоугольный.
Случай 3. а = b. В этом случае треугольник ABC равнобедренный. Такой треугольник можно решить, разбразбив его высотой CD на два прямоугольных треугольника:
В = А; С = 180° — 2А; с = 2AD = 2а cos A.
Пример. Вычислить стороны и углы треугольника, если дано:
(деление на 73,5 можно заменить умножением на 1 /73,5 ≈ 0,0136).
Так как в данном случае а b sin A /a а + b, то треугольник с данными сторонами не существует. Будем считать, что с 2 =b 2 + с 2 — 2bc cos А
b 2 =c 2 + a 2 — 2ca cos B, откуда
Угол А острый, так как он лежит против меньшей стороны; следовательно,
Точно также ( B = arcsinfrac ) и, наконец, С = 180° — (А + В)
Итак, при решении треугольника по трём сторонам при помощи логарифмических таблиц углы, лежащие против меньших сторон, находятся по формулам, а угол, лежащий против наибольшей стороны, вычисляется как разность между 180° и суммой двух найденных углов.
Пример. Решить треугольник, зная длины (приближенные) его сторон: 24,7; 22,4 и 31,3. Обозначим a ≈ 22,4; b ≈ 24,7; с ≈ 31,3.
Решение при помощи натуральных таблиц. Имеем:
откуда А ≈ 45°20’ (с округлением до 10’).
откуда В ≈ 51°30’ и, наконец, С ≈ 180° — (45°20’ + 51°30’) ≈ 83°10’.
Решение при помощи логарифмических таблиц. Имеем:
sin А = 2S /bc, lg sin А = lg 2S — lg b — lg c.
🔍 Видео
№63. Даны два равных угла. Равны ли смежные с ними углы?Скачать

Два угла треугольникаСкачать

Найдите третью сторону треугольникаСкачать

№169. Даны два двугранных угла, у которых одна грань общая, а две другие грани являютсяСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Задача, которую боятсяСкачать

Найдите угол: задача по геометрииСкачать

Нахождение стороны прямоугольного треугольникаСкачать

Вычисляем угол через координаты вершинСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать