О чем эта статья:
- Касательная к окружности, секущая и хорда — в чем разница
- Свойства касательной к окружности
- Задача
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Окружность ab касательная найти радиус
- Радиус — что это такое и как найти радиус окружности
- Через длину стороны
- Найти радиус круга, зная окружность
- Радиус и диаметр
- Вычисление радиуса
- Если известен диаметр
- Если известна длина окружности круга
- Если известна площадь круга
- Способ расчета радиуса круга:
- Через сторону описанного квадрата
- Как посчитать радиус зная длину окружности
- Формула
- Свойства радиуса
- По площади сектора и центральному углу
- Площадь сегмента
- Формулы для площади круга и его частей
- Центральный угол, вписанный угол и их свойства
- Связанные определения
- Примеры задач
- Длина дуги
- Уравнение окружности
- Задача
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Дано окружность ab касательная найти радиус окружности
Видео:Найти центр и радиус окружностиСкачать

Касательная к окружности, секущая и хорда — в чем разница
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
| |||
| Окружность круга P | |||
| Результат | |||
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |

где R – радиус круга, D – диаметр круга


если величина угла α выражена в радианах

если величина угла α выражена в градусах


если величина угла α выражена в радианах

если величина угла α выражена в градусах
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга


если величина угла α выражена в радианах

если величина угла α выражена в градусах


если величина угла α выражена в радианах

если величина угла α выражена в градусах
Видео:Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Центральный угол, вписанный угол и их свойства
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Связанные определения
- Центральный угол в окружности — это угол , образованный двумя радиусами.
- Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.
Видео:Радиус окружности с центром в точке O равен 85 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Видео:№636. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиесяСкачать
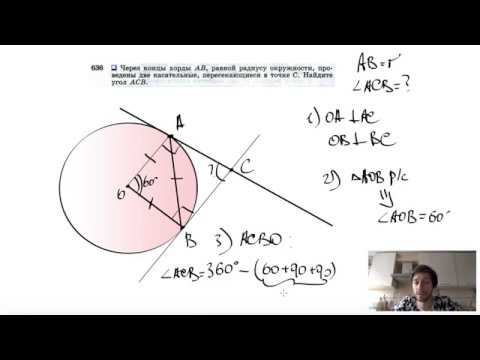
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла .
В случае, когда величина α выражена в градусах , справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах , справедлива пропорция
из которой вытекает равенство:
Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Уравнение окружности
r 2 = ( x – a ) 2 + ( y – b ) 2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами ( a, b ) в декартовой системе координат:
| АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания. Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ. Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом. ЗадачаУ нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ. Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°. Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла. ∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62° Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°. Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны. Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD. Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°. Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны. Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам. Задача 1У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные. Решение Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA. ∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°). Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами: ∠BDC = ∠BDA × 2 = 30° × 2 = 60° Итак, угол между касательными составляет 60°. Задача 2К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК. Решение Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным. Углы при его основании будут равны, т.е. ∠МNК = ∠NМК. ∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65° Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть. Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения. Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей. Задача 1Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA. Решение Исходя из соотношения касательной и секущей МА 2 = МВ × МС. Найдем длину внешней части секущей: МС = МВ — ВС = 16 — 12 = 4 (см) МА 2 = МВ × МС = 16 х 4 = 64 Задача 2Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO. Решение Допустим, что МО = у, а радиус окружности обозначим как R. В таком случае МВ = у + R, а МС = у – R. Поскольку МВ = 2 МА, значит: МА = МВ : 2 = (у + R) : 2 Согласно теореме о касательной и секущей, МА 2 = МВ × МС. (у + R) 2 : 4 = (у + R) × (у — R) Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим: Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см). Ответ: MO = 10 см. Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними. Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC. Задача 1Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой. Решение Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ. АВ = ∠АВС × 2 = 32° × 2 = 64° Задача 2У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK. Решение Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно: КМ = 2 ∠МКВ = 2 х 84° = 168° Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный. ∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2 Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то: ∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6° Видео:Окружность, касательная, секущая и хорда | МатематикаСкачать  К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85Ваш ответрешение вопросаПохожие вопросы
Популярное на сайте: Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так. Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. Дано окружность ab касательная найти радиус окружностиК окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см. Решение . Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB. Из теоремы Пифагора: |