Через точку р лежащую в центре окружности

Геометрия | 5 — 9 классы

Через точку А, находящуюся на расстоянии 5 см от центра окружности радиуса 11 см, проведена хорда, которую точка А делит в отношении 2 : 3.

Найдите длину этой хорды.

Расстояние между точками О и А : ОA = 5 (дано).

Хорда BC = BA + AC или BC = 2х + 3х = 5х.

Радиус DO = OE = 11 (дано).

DA = DO + OA или DA = 16см.

АЕ = ОЕ — ОА или АЕ = 6см.

По свойству пересекающихся хорд DA * AE = 2X * 3X или

(DO + OA) * AE = 6X² или 16 * 6 = 6X².

Отсюда Х = 4см и хорда

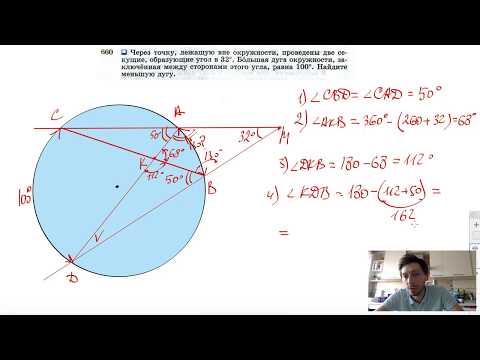
Видео:№660. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32Скачать

Постройте окружность?

Длина хорды 16см.

Центр хорды удалён от центра окружности на 6 см.

Вычислите радиус и диаметр окружности.

Видео:через точку А, лежащую вне окружности проведены две прямые. Одна прямая касается.. ФИПИСкачать

Через точку М, находящуюся на расстоянии 15см от центра окружности радиусом 17 см, проведена хорда CD, которая делится точкой М на отрезки CM : MD = 1 : 4?

Через точку М, находящуюся на расстоянии 15см от центра окружности радиусом 17 см, проведена хорда CD, которая делится точкой М на отрезки CM : MD = 1 : 4.

Найдите хорду CD.

Видео:Через точку A, лежащую вне окружности, проведены две прямые.Скачать

Через точку Р, лежащую внутри окружности, проведена хорда, которая делится точкой Р на отрезки, длины которых равны 4 см и 5 см?

Через точку Р, лежащую внутри окружности, проведена хорда, которая делится точкой Р на отрезки, длины которых равны 4 см и 5 см.

Найдите расстояние от точки Р до Центра окружности, если её радиус равен 6 см.

Видео:Уравнение окружности (1)Скачать

Через точку М, находящуюся на расстоянии 15 см от центра окружности, проведена хорда, которая делится точкой М в отношении 1 : 4?

Через точку М, находящуюся на расстоянии 15 см от центра окружности, проведена хорда, которая делится точкой М в отношении 1 : 4.

Радиус окружности равен 17 см.

Найти длину этой хорды.

Пожалуйста с рисунком.

Видео:Геометрия Через точку A, лежащую вне окружности, проведены две прямые, одна из которых пересекаетСкачать

Через точку А, находящующуюся на расстоянии 5 см от центра на окружности, радиуса 11 см проведена хорда, которую точка А делит на отрезки длины, которых относятся как 2 : 3?

Через точку А, находящующуюся на расстоянии 5 см от центра на окружности, радиуса 11 см проведена хорда, которую точка А делит на отрезки длины, которых относятся как 2 : 3.

Найдите длину этой хорды.

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Диаметр СD окружности с центром в точке О пересекается с хордой AB в точке К, OK = 5 см?

Диаметр СD окружности с центром в точке О пересекается с хордой AB в точке К, OK = 5 см.

Расстояние от центоа окружности до хорды равно 4см.

Найдите радиус окружности, если длина хорды равна 16 см.

Видео:Геометрия Через точку A, лежащую вне окружности, проведены две прямые, одна из которых касаетсяСкачать

Точка M удалена на 20 см от центра окружности, радиус которой равен 22 см?

Точка M удалена на 20 см от центра окружности, радиус которой равен 22 см.

Через эту точку проведена хорда длинной 20 см.

Найдите длины отрезков, на которые делит точка M данную хорду.

Видео:Геометрия Через точку A, лежащую вне окружности с центром в точке O, проведены две прямые, однаСкачать

В окружности проведена хорда длинной 10 см?

В окружности проведена хорда длинной 10 см.

Радиус окружности равен 13 см.

Найдите расстояние от центра окружности до хорды.

Видео:Геометрия Дана точка Р, удаленная на 7 см от центра окружности радиуса 11 см. Через эту точкуСкачать

Проведена окружность с центром в точке О?

Проведена окружность с центром в точке О.

Хорда АВ = 10 см, угол АОВ = 90°.

Найдите расстояние от точки О до хорды АВ.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см?

Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см.

На этой странице вы найдете ответ на вопрос Через точку А, находящуюся на расстоянии 5 см от центра окружности радиуса 11 см, проведена хорда, которую точка А делит в отношении 2 : 3?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Решение на картинках. Удачи! : ).

Дано : угол 1 — угол 2 = 10° Найти : углы 1, 2, 3, 4. Решение : Пусть угол 2 — x, тогда угол 1 — x + 10°. X + x + (x + 10°) + (x + 10°) = 360° 4x + 20° = 360° 4x = 360° — 20° 4x = 340° x = 340° / 4 x = 85° — углы 2, 4 2)85° + 10° = 95° — углы 1, 3.

Дано : ABCD — параллелограмм, АВ = CD = 9 см, ВС = AD = 15 см, BD перпендикулярно АВ. Найти : S. Решение 1) ∆ABD, угол ABD = 90°. По теореме Пифагора BD = √(AD² — AB²) = √(15² — 9²) = √((15 — 9)(15 + 9)) = √(6×24) = √(6×6×4) = √(6²×2²) = 6 * 2 = 1..

По теореме синусов. АВ / sinC = AC / sinB √3 : (√3 / 2) = √2 : sin B⇒ sin B = √2 / 2 — это синус 45° Угол В = 45°.

Мы знаем, что сумма смежных углов равна 180°, тогда пусть х — это то на сколько угол поделили, для того чтобы получились цыфры 3 и 15 (умными словами это називается коефициент пропорциональности), тогда составим уравнение : 3х + 15х = 180 18х = 180 х..

2, 6 градуса смежных углов.

Трапеция равнобоковая и ее боковые стороны равны . Углы при основании равны. Треугольники образованные высотами проведенными к большему основанию то же. (гипотенуза и острый угол одного гипотенузе и острому углу другого). Высоту и диагональ образ..

A² = 3b² a = b√3 P₁ = 4b P₂ = 4b√3 P₂ / P₁ = 4b√3 / 4b = √3 Ответ отношение их периметров√3.

180º(развернутый угол) — 130º(угол при вершине) = 50º ; далее из 180º(сумма углов в треугольнике) — 50º = 130 — сумма углов при основании, т. К треугольник равнобедренный, то углы при основании равны. Следовательно меньший угол можно получить путем..

1)ОС = ОВ Кут ВСО = Куту СВО = 35 градусів кут ОВА = 90 градусів кут АВС = 90 — 35 = 55 градусів.

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Касательная к окружности

О чем эта статья:

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

Видео:Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

🔥 Видео

№150. Даны окружность, точка А, не лежащая на ней, и отрезок PQ. Постройте точку М на окр-тиСкачать

Построение прямой, параллельной даннойСкачать

Окружность. 7 класс.Скачать

№964. На окружности, заданной уравнением (x-3)2 + + (y-5)2 = 25, найдите точки: а) с абсциссой 3;Скачать

Геометрия Хорда MK окружности делится точкой P на два отрезка длиной 8 см и 12 см. НайдитеСкачать

Задача по темам: окружность, равнобедренный треугольник. "Окружности с центрами в точках Р и Q ..."Скачать