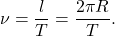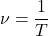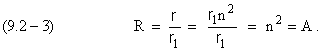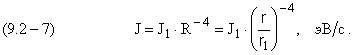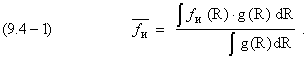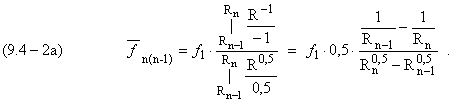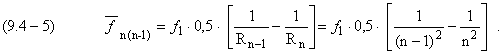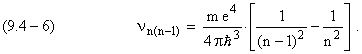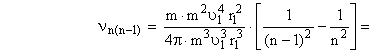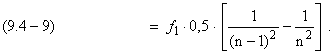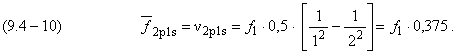Частота обращения электрона по окружности (4 видео)

Движение по окружности, период обращения и частота.

1. Равномерное движение по окружности

Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.

Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.

Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.

Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке.

Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.

2. Период вращения и вращающаяся частота

Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.

Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.

Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.

При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:

Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: . Итак,

Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:

частота вращения равна количеству полных оборотов за одну секунду.

Частота вращения и период обращения связаны следующим соотношением:

Частоту в СИ измеряют в

3. Вращательное движение

В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.

Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.

Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

ПРОВЕРЬТЕ СЕБЯ

Приведите два-три примера криволинейного движения.
Приведите два-три примера равномерного движения по кругу.
Что такое вращательное движение? Приведите примеры такого движения.
Как направлена мгновенная скорость при движении по кругу Приведите два-три примера.

1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.

2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением: Частоту в СИ измеряют в обратных секундах.

3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

Содержание

Частота обращения электрона по окружности
5.1 Cредняя частота излучения электрона для круговых орбит в переходе
Цена книги 90 рублей.
Как определить период вращения
Номинальная скорость вращения
Угловая скорость
Угловая скорость в конкретных случаях
Как определить угловую скорость
Угол поворота и период обращения
Циклическая частота вращения (обращения)
Переход от угловой к линейной скорости
Видео
Видео

Видео:Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Частота обращения электрона по окружности

5. ЧАСТОТА ИЗЛУЧЕНИЯ ФОТОНА

СОВПАДАЕТ СО СРЕДНЕЙ ЧАСТОТОЙ ИЗЛУЧЕНИЯ

ЭЛЕКТРОНА В ПЕРЕХОДЕ

(Представленный материал соответсвует главе 9 книги 5 )

Теория атома водорода, развиваемая автором, возвращает логику и механику в границы конкретной научной модели. Оказалось, что переход электрона между стационарными орбитами можно описать классическими формулами, причем результаты хорошо совпадают с квантовыми формулами и с эмпирическими данными. Дальнейшие исследования в этом направлении могут иметь стратегическое значение для «водородной энергетики», которая идет на смену «углеводородному топливу».

5.1 Cредняя частота излучения электрона для круговых орбит в переходе

Рассмотрен наиболее простой случай движения электрона в переходе по круговым, спирально уменьшающимся орбитам. В параграфах 5.1.1 ÷ 5.1.3 показано, что средняя частота, излучаемая электроном в переходе, равна частоте фотона, испущенного в этом переходе.

5.1.1 ДВИЖЕНИЕ ЭЛЕКТРОНА В ПЕРЕХОДЕ

1. Рассмотрим переходы электрона между соседними, круговыми стационарными орбитами в атоме водорода.

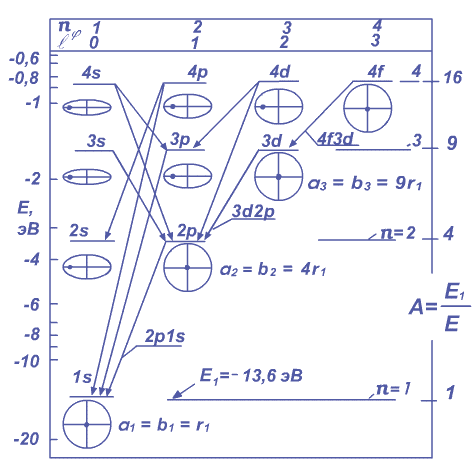
Это переходы 2p1s, 3d2p, 4f3d и т.д. Они показаны на Рисунке 9.2.1, где по оси ординат слева дана энергия Е электрона в электрон-вольт (эВ).

По оси ординат справа дано «относительное» значение энергии электрона

– энергия электрона на первой, круговой стационарной орбите, в 1s состоянии,

, E – стационарное и текущее значение энергии электрона в переходе,

A – относительное значение большой полуоси а орбиты,

b – малая полуось орбиты электрона,

– радиус первой, круговой стационарной орбиты,

n – стационарное (целое) и текущее значение главного квантового

числа в переходе.

По оси абсцисс (показана сверху) приведены значения азимутального квантового числа Зоммерфельда и орбитального квантового числа ℓ Ланде.

Рисунок 9.2.1. Схема энергетических уровней и излучательных переходов в атоме водорода Бора – Зоммерфельда. Иллюстративно показаны эллиптические и круговые орбиты электрона вокруг ядра. Большие полуоси орбит даны условно одного размера.

2. В процессе перехода между соседними, круговыми стационарными орбитами электрон движется по круговым, спирально уменьшающимся орбитам с текущим радиусом r. Определяя среднюю частоту излучения, испускаемого электроном в течение перехода, будем обращаться к 2p1s переходу, дающего первую линию серии Лаймана (Рисунок 9.2.1).

Частота обращения электрона вокруг ядра в переходе возрастает по мере уменьшения относительного радиуса R орбиты и по мере уменьшения главного квантового числа n [ 9.2.1 ] :

– частота обращения электрона вокруг ядра по первой, круговой

стационарной орбите в атоме водорода,

– частота излучения энергии электроном в переходе,

согласно электродинамике, увеличивается соответственно

росту текущей частоты обращения электрона :

Так в начале 2p1s перехода, при , текущая частота обращения и излучения

а в конце перехода ( ) эти частоты в восемь раз выше:

Интенсивность J излучения электрона на текущей круговой орбите [ 9.2.2 ]

– интенсивность излучения, которую согласно электродинамике должен испускать электрон на первой, круговой стационарной орбите в атоме водорода.

Двигаясь в переходе по круговым, спирально уменьшающимся орбитам, электрон испускает текущую частоту излучения с нарастающей интенсивностью, т.к. n и R уменьшаются.

9.2.1 ) Шидловский А.И. Атом водорода — самый простой из атомов .

Минск: ВЭВЭР, 1997. С. 32.

9.2.2 ) Шидловский А.И. Атом водорода — самый простой из атомов .

Минск: ВЭВЭР, 1997. С. 90.

5.1.2 УДЕЛЬНАЯ АМПЛИТУДА ВОЛНЫ ИЗЛУЧЕНИЯ ЭЛЕКТРОНА

При усреднении частот складываются амплитуды G волн излучения, а не их интенсивности J. Амплитуда волны связана с интенсивностью квадратичной зависимостью [ 9.3.1 ] .

На n-ой круговой стационарной орбите амплитуда волны с учетом (9.2-7):

, .

При движении электрона вокруг ядра характерным временем является период обращения и равный ему период излучения энергии электроном.

– период обращения электрона вокруг ядра по первой,

круговой стационарной орбите [ 9.3.2 ] .

Для круговой, n-ой стационарной орбиты запишем выражение удельной амплитуды волны, которая излучается в течение периода обращения :

– удельная амплитуда волны излучения, которую согласно электродинамике,

должен испускать электрон на первой, круговой стационарной орбите

в течение периода обращения .

Величина g имеет размерность действия в степени 0,5. Она характеризует частость («интенсивность») излучения частоты , определяемой по (9.2-4), в течение периода Т.

В процессе перехода электрона между n-ой и (n –1)-ой круговыми стационарными орбитами удельная амплитуда волны излучения с учетом (9.3-3) и (9.2-3):

Отношение удельных амплитуд на (n –1)-ой и более дальней соседней n-ой круговой стационарной орбите

Наибольшее значение (9.3-5), равное двум, соответствует 2p1s переходу, а для перехода , например, оно снижается до .

Таким образом, удельная амплитуда волны излучения g сравнительно слабо изменяется в течение перехода электрона между соседними круговыми стационарными орбитами.

9.3.1 ) Бутиков Е.И. Оптика.

М.: Высшая школа, 1986. С. 32.

9.3.2 ) Шидловский А.И. Атом водорода — самый простой из атомов .

Минск: ВЭВЭР, 1997. С. 32.

9.3.3 ) Шидловский А.И. Атом водорода — самый простой из атомов .

Минск: ВЭВЭР, 1997. С. 90.

9.3.4 ) Шидловский А.И. Атом водорода — самый простой из атомов .

Минск: ВЭВЭР, 1997. С. 105.

9.3.5 ) Шидловский А.И. Атом водорода — самый простой из атомов .

Минск: ВЭВЭР, 1997. С.16-17. С. 105.

5.1.3 СРЕДНЯЯ ЧАСТОТА ИЗЛУЧЕНИЯ ЭЛЕКТРОНА

1. В течение перехода между n-ой и (n –1)-ой соседними круговыми стационарными орбитами частота излучения электрона по (9.2-4) имеет непрерывное распределение своих значений от до .

Для определения средней частоты применим выражение теории вероятностей

[ 9.4.1 ]

Здесь в числителе – сумма произведений текущей частоты излучения на её «вес» (частость), а в знаменателе сумма «весов» всех частот.

Подставляя в (9.4-1) по (9.2-4) и g по (9.3-4), определим среднюю частоту излучения электрона, испускаемую им в результате перехода между n-ой и (n –1)-ой круговыми стационарными орбитами:

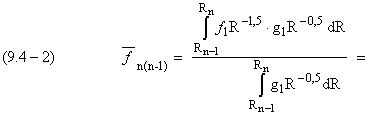
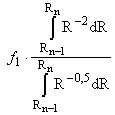
Интегрируя (9.4-2), получим

Для круговой стационарной орбиты по (9.2-3)

Тогда знаменатель (9.4-2а) упрощается

и для (9.4-2а) получим

2. Сопоставим выражение (9.4-5) для средней частоты излучения электрона в переходе с формулой Бора для частоты излучения фотона этого перехода.

В случае перехода электрона между n-ой и (n–1)-ой круговыми стационарными орбитами формула Бора дает для частоты излучения фотона [ 9.4.2 ] :

m , e – масса и заряд электрона,

– запись постоянной Планка.

Упростим (9.4-6), используя выражения теории Бора [ 9.4.3 ] :

– скорость электрона на первой, круговой стационарной орбите с радиусом .

Подставим в (9.4-6) выражения (9.4-7) и (9.4-8)

Таким образом, в случае перехода электрона по круговым, спирально уменьшающимся орбитам выражение (9.4-5) для средней частоты излучения электрона совпадает с формулой Бора для частоты излучения фотона, полученной им в 1913 году на основе использования закона сохранения энергии.

Выражение (9.4-5) для средней частоты излучения

электрона получено здесь с помощью представления о вращении электрона вокруг ядра в переходе по круговым спирально уменьшающимся орбитам и использования среднего значения теории вероятностей.

Для 2p1s перехода можно записать с учетом (9.4-5):

Следовательно, дан частично ответ на вопрос Лоренца о механизме образования света «согласно теории Бора». Показано, что в случае перехода электрона между соседними круговыми стационарными орбитами его средняя частота излучения в переходе совпадает с частотой излучения фотона этого перехода.

9.4.1 ) Шпольский Э.В. Атомная физика.

Т.1 . М.: Наука, 1984. С. 534.

9.4.2 ) Собельман И.И. Введение в теорию атомных спектров .

М.: Наука, 1977. С. 15.

9.4.3 ) Шидловский А.И. Атом водорода — самый простой из атомов.

Минск: ВЭВЭР, 1997. С. 16, 21.

ОБЗОР ГЛАВ 10, 11, 12, 13 КНИГИ 5

В Главах девятой, десятой и одиннадцатой книги 5 сделана попытка в решении вопроса, поставленного в 1923 году нобелевским лауреатом Лоренцем: «…в конце концов как образуется свет согласно теории Бора». [ 5.1 ] .

Рассмотрены переходы, приводящие к образованию линий серии Лаймана и Бальмера. Переходы электрона происходят между стационарными орбитами.

В течение перехода электрон движется вокруг ядра по круговым или эллиптическим, спирально уменьшающимся орбитам.

Используется наглядная модель движения электрона и применяется простая математика.

1. Введена удельная амплитуда волны излучения, характеризующая излучение электрона в течение периода обращения его по орбите.

2. Определено средствами классической физики среднее расстояние электрона от ядра на эллиптической орбите. Оно оказалось близким по аналитическому выражению к среднему расстоянию, найденному квантовой механикой.

3. Оценено число оборотов электрона вокруг ядра в переходе и время перехода электрона.

4. Время перехода электрона сопоставлено со временем жизни перехода по данным квантовой механики. В целом, получена корреляция значений сопоставляемых величин, хотя физический смысл их несколько различен.

5. Для спектральных линий серии Лаймана и Бальмера определена средняя частота излучения энергии электроном в течение перехода, которая оказалась равной частоте излучения фотона этого перехода. В этом случае дается, по-видимому, частичный ответ на вопрос Лоренца. Остается не ясным механизм «концентрирования» излучения электрона в течение перехода в направленное излучение фотона.

Остается по-прежнему неясным причина отсутствия дипольного излучения электрона в стационарных состояниях (на стационарных орбитах).

В Главе двенадцатой рассмотрена важная величина – действие применительно к стационарным орбитам электрона.

1. Используя орбитальные характеристики при движении электрона по стационарным орбитам, определено действие в форме Лагранжа, Мопертюи и Гамильтона.

2. Вычислены составляющие действия, определяемые переносной и радиальной скоростью электрона для стационарных орбит. Эти составляющие в теории Бора – Зоммерфельда были постулированы.

3. Согласно механике, полученное постоянное значение действия для электрона на стационарной орбите указывает, по-видимому, что это движение является фактическим, среди других кинематически возможных движений.

В Главе тринадцатой ( в порядке обсуждения) рассмотрена гипотетическая серия линий, обусловленная переходами электрона с ns уровней на протон р ядра атома водорода. В качестве примера рассмотрен гипотетический 2sp переход.

Наша работа может привлечь внимание специалистов атомной физики, исследователей, студентов, заинтересованных читателей.

5.1 ) Джеммер М. Эволюция понятий квантовой механики .

М.: Наука, 1985. С. 158.

Подробно данный материал изложен в книге:

Продолжение теории Нильса Бора. М.: Издательство ЛКИ , 2007. – 144 С.

Цена книги 90 рублей.

Автор с признательностью примет замечания и предложения

по адресу: 127576, Москва, ул. Череповецкая, д. 14, кв. 168,

по телефону: 8(499) 200-94-28,

Шидловскому Александру Игнатьевичу.

По вопросу приобретения опубликованных книг можно обратиться по указанному здесь адресу.

Видео:Период и частота обращенияСкачать

Как определить период вращения

Равномерное движение по окружности характеризуют периодом и частотой обращения.

Период обращения — это время, за которое совершается один оборот.

Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле:

Итак, чтобы найти период обращения, надо время, за которое совершено п оборотов, разделить на число оборотов.

Другой характеристикой равномерного движения по окружности является частота обращения.

Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:

Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.

За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с -1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.

Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому

Формулы (6.1) и (6.3) позволяют найти период обращения Т, если известны число n и время оборотов t или частота обращения V. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела V и радиус окружности r, по которой оно движется.

Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (lокр = 2 Пr, где П≈3,14- число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,

Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.

. 1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?

Отослано читателями из интернет-сайтов

_{Сборник конспектов уроков по физике, рефераты на тему из школьной программы. Календарно тематическое планирование. физика 8 класс онлайн, книги и учебники по физике. Школьнику подготовиться к уроку.}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

Количество повторений каких-либо событий или их возникновения за одну единицу таймера называется частотой. Это физическая величина измеряется в герцах – Гц (Hz). Она обозначается буквами ν, f, F, и есть отношение количества повторяющихся событий к промежутку времени, в течение которого они произошли.

При обращении предмета вокруг своего центра можно говорить о такой физической величине, как частота вращения, формула:

где:

N – количество оборотов вокруг оси или по окружности,
t – время, за которое они были совершены.

В системе СИ обозначается как – с-1 (s-1) и именуется как обороты в секунду (об/с). Применяют и другие единицы вращения. При описании вращения планет вокруг Солнца говорят об оборотах в часах. Юпитер делает одно вращение в 9,92 часа, тогда как Земля и Луна оборачиваются за 24 часа.

Видео:Физика - движение по окружностиСкачать

Номинальная скорость вращения

Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:

К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.

Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.

Видео:Урок 87 (осн). Вращательное движение. Период и частота вращенияСкачать

Угловая скорость

Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.

Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.

Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:

где:

ω – угловая скорость (рад./с);
∆ϕ – изменение угла отклонения при повороте (рад.);
∆t – время, затраченное на отклонение ©.

Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.

Угловая скорость в конкретных случаях

На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.

Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.

где:

π – число, равное 3,14;
ν – частота вращения, (об./мин.).

В качестве примера могут быть рассмотрены угловая скорость и частота вращения колёсного диска при движении мотоблока. Часто необходимо уменьшить или увеличить скорость механизма. Для этого применяют устройство в виде редуктора, при помощи которого понижают скорость вращения колёс. При максимальной скорости движения 10 км/ч колесо делает около 60 об./мин. После перевода минут в секунды это значение равно 1 об./с. После подстановки данных в формулу получится результат:

ω = 2*π*ν = 2*3,14*1 = 6,28 рад./с.

К сведению. Снижение угловой скорости часто требуется для того, чтобы увеличить крутящий момент или тяговое усилие механизмов.

Как определить угловую скорость

Принцип определения угловой скорости зависит от того, как происходит движение по окружности. Если равномерно, то употребляется формула:

Если нет, то придётся высчитывать значения мгновенной или средней угловой скорости.

Величина, о которой идёт разговор, векторная, и при определении её направления используют правило Максвелла. В просторечии – правило буравчика. Вектор скорости имеет одинаковое направление с поступательным перемещением винта, имеющего правую резьбу.

Рассмотрим на примере, как определить угловую скорость, зная, что угол поворота диска радиусом 0,5 м меняется по закону ϕ = 6*t:

ω = ϕ / t = 6 * t / t = 6 с-1

Вектор ω меняется из-за поворота в пространстве оси вращения и при изменении значения модуля угловой скорости.

Видео:Физика.Узнать за 2 минуты.Основные понятия.Что такое частотаСкачать

Угол поворота и период обращения

Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.

Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать ½, ¼ оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.

Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.

Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.

В этом случае находят применения такие характеристики, как:

период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.

Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.

Видео:потомучто Откуда электрон берет энергию чтобы вечно вращаться вокруг ядраСкачать

Циклическая частота вращения (обращения)

Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.

Циклическая частота вращения – это количество оборотов тела за 2*π секунды.

У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.

Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.

При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:

частоты питающей сети;
количества пар полюсов.

Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Переход от угловой к линейной скорости

Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:

ν = 2*π*R / Т = 2*π*R* ν.

Так как ω = 2*π*ν, то получается:

Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.

К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.

Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:

а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.

Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.

Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.

Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать