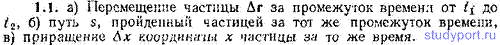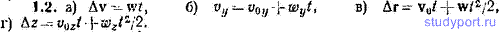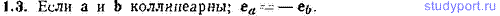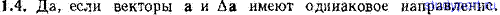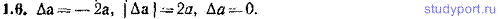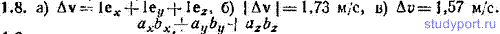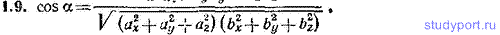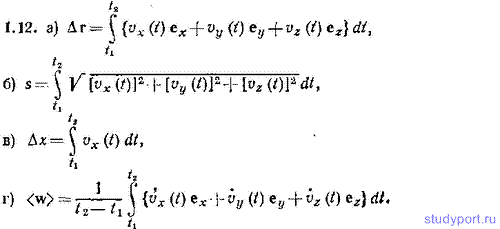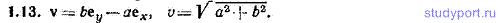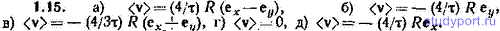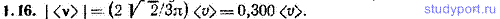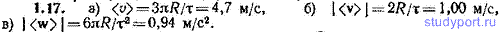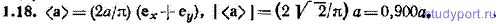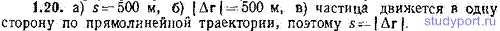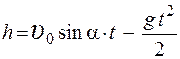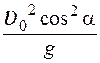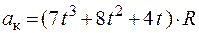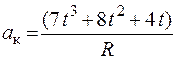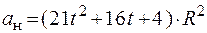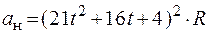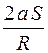1.1. Частица движется с постоянной скоростью v. Что определяет выражение: a) v(t2-t1), б) v(t2-t1), в) vx(t2-t1)?
1.2. Частица движется с постоянным ускорением w. В начальный момент времени она находилась в точке с радиус-вектором r0 и имела скорость v0. Написать выражение для: а) приращения скорости частицы dv за время t, б) проекции скорости частицы на ось у в момент времени t, в) перемещения частицы за время t, г) приращения координаты z частицы за время.
1.3. В каком случае векторы а и b могут быть связаны соотношением a = αb, где α — скаляр? Как соотносятся их орты, если а0?
1.4. Может ли приращение модуля вектора Δа оказаться равным модулю приращения вектора |Δа|?
1.5. В каком соотношении находятся приращение модуля вектора и модуль приращения вектора |Δа|, если векторы а и Δа направлены в противоположные стороны?
1.6. Вектор а изменил направление на обратное. Найти: Δa, |Δa|, Δa.
1.7. Вектор а повернулся без изменения «длины» на малый угол δφ. а) Написать приближенное выражение для |Δа|. б) Чему равно Δа?
1.8. Начальное значение скорости равно v1=1ex+3ey+5ez (м/с), конечное v2=2ex+4ey+6ez (м/с). Найти: а) приращение скорости Δv, б) модуль приращения скорости |Δv|, в) приращение модуля скорости Δv.
1.9. Написать выражение для косинуса угла α между векторами с компонентами ax, ay, az и bx, by, bz.
1.10. Компоненты одного вектора равны (1, 3, 5), другого — (6, 4, 2). Найти угол α между векторами.
1.11. Преобразовать к виду, содержащему только модули векторов и угол α, выражение a [bc], в котором векторы а и с взаимно перпендикулярны, а вектор b образует с нормалью к плоскости, в которой лежат векторы а и с, угол α.
1.12. Заданы функции vx(t), vy(t) и vz(t), определяющие в некоторой системе координат скорость частицы v. Написать выражение для: а) перемещения частицы Δr за промежуток времени от t1 до t2, б) пути s, пройденного частицей за тот же промежуток времени, в) приращения Δх координаты х частицы за время от t1 до t2. г) среднего значения ускорения частицы за то же время.
1.13. Частица 1 движется со скоростью v1 = aex, частица 2 — со скоростью v2=bey (a и b — константы). Найти скорость v второй частицы относительно первой и модуль v этой скорости.
1.15. Частица движется равномерно по часовой стрелке по окружности радиуса R, делая за время τ один оборот. Окружность лежит в координатной плоскости x, y, причем центр окружности совпадает с началом координат. В момент t = 0 частица находится в точке с координатами x = 0, y = R. Найти среднее значение скорости точки за промежуток времени: а) от 0 до τ/4, б) от 0 до τ/2, в) от 0 до 3τ/4, г) от 0 до τ, д) от τ/4 до 3τ/4.
1.16. Частица прошла за некоторое время 3/4 окружности со средним значением модуля скорости (v). Найти модуль средней скорости частицы | | за то же время.
1.17. Первоначально покоившаяся частица прошла за время 10,0 с полторы окружности радиуса 5,00 м с постоянным тангенциальным ускорением. Вычислить соответствующие этому промежутку времени значения: а) среднего модуля скорости , б) модуля средней скорости | |, в) модуля среднего ускорения | |.
1.18. Постоянный по модулю вектор а, равномерно поворачиваясь против часовой стрелки в плоскости х, у, переходит за время из положения, при котором он совпадает по направлению с осью х, в положение, при котором он совпадает по направлению с осью у. Найти среднее за время значение вектора а и модуль этого среднего.
1.19. Радиус-вектор точки r изменяется: а) только по модулю, б) только по направлению. Что можно сказать о траектории?
1.20. Радиус-вектор частицы определяется выражением: r=3t 2 ex+4t 2 ey+7ez (м). Вычислить: а) путь s, пройденный частицей за первые 10 секунд движения, б) модуль перемещения |Δr| за то же время, в) объяснить полученные результаты.
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Кинематика поступательного и вращательного движения
Содержание
1. Кинематика поступательного и вращательного движения. 5
2. Динамика поступательного и вращательного движений. 11
3. Механические колебания и волны. 21
4. Молекулярная физика и термодинамика. 31
ВВЕДЕНИЕ
В сборнике представлены тестовые задания закрытого типа и на соответствие по разделу «Физические основы механики. Молекулярная физика и термодинамика» дисциплины «Физика», предназначенные для аудиторной и внеаудиторной самостоятельной работы студентов.
Тестовые задания сгруппированы по темам «Кинематика поступательного и вращательного движения», «Динамика поступательного и вращательного движений», «Механические колебания и волны», «Молекулярная физика и термодинамика».
Содержание тестовых заданий направлено на формирование у студентов знания физических явлений, законов, формул, единиц измерения физических величин, умения применять законы и формулы для решения качественных и расчетных задач, графически представлять физические явления и законы, анализировать их.
В тестовых заданиях закрытой формы из 3-5 приведенных ответов следует выбрать правильный. В заданиях на соответствие необходимо установить соответствие элементов одного множества элементам другого. Тестовые задания такой формы сопровождаются инструкцией «Установить соответствие».
Самостоятельная работа студентов с тестовыми заданиями поможет при подготовке к лабораторным и практическим занятиям, а также будет способствовать более глубокому изучению раздела дисциплины «Физика» «Физические основы механики. Молекулярная физика и термодинамика».
Кинематика поступательного и вращательного движения
1.Материальная точка движения так, что радиус-вектор меняется со временем по закону 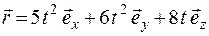

1. 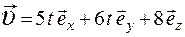
3. 
5.
2.Материальная точка движется согласно уравнению 
1. 48 2. 24 3. 5 4. 2 5. 0
3.Радиус-вектор частицы определяется выражением 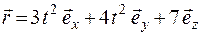
1. 707 2. 500 3. 150 4. 100 5. 25
4.Частица за некоторое время прошла 3/4 окружности со средним значением модуля скорости 
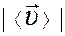
1. 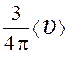

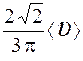
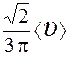
5.Радиус-вектор частицы изменяется со временем по закону 
1. 14 2. 8 3. 8,8 4. 12,6 5. 10
6.Вектор средней скорости материальной точки совпадает по направлению с
1. радиус-вектором, определяющим положение точки
2. вектором полного ускорения
3. вектором нормального ускорения
4. касательной к траектории
5. вектором перемещения
7.Частица движется со скоростью 
1. 13,5 2. 5,38 3. 24,3 4. 27 5. 9
 |
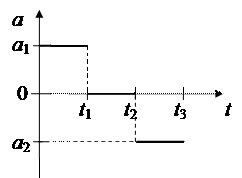
8.Зависимость скорости движения материальной точки по прямой от времени дана на рисунке. Среднее значение модуля скорости движения материальной точки в интервале времени 0-5 с равна (м/с)
1. 1,5 2. 0,25 3. 2,5 4. 0,2 5. 1,4
 |
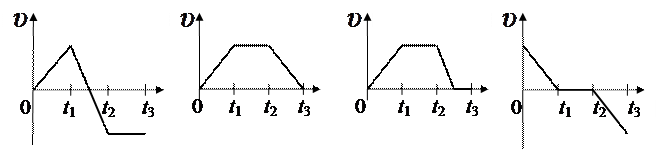
9.На рисунке приведен график зависимости ускорения тела от времени
График зависимости скорости тела от времени имеет вид
1. а 2. б 3. в 4. г

Зависимость пути, пройденного телом, от времени, представлена на графике
1. а 2. б 3. в 4. г
11. От движущегося поезда отцепляют последний вагон, который вследствие трения останавливается, а поезд продолжает двигаться с прежней скоростью 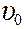
1. 2 2. 4 3. 1 4. 0,5 5. 0,1
12.Две материальные точки движутся согласно уравнениям 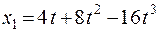

1. 0,23 2. 0,542 3. 0,845 4. 0,9 5. 1
13. Тело брошено с начальной скоростью 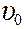
1. 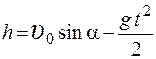
3. 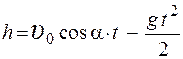
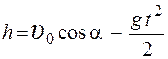
14.Тело брошено под углом α к горизонту. Чтобы максимальная высота подъема тела была равна дальности полета, угол α должен быть равен (град)
1. 30 2. 60 3. 45 4. 76 5. 84
15.Тело брошено под углом α к горизонту с начальной скоростью 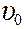
1. 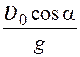

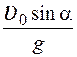


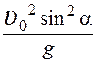
16.Тело брошено под углом α к горизонту с начальной скоростью 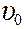
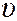
1. 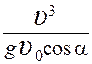

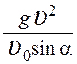
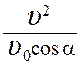
17.Мяч брошен под углом 60° к горизонту с начальной скоростью 10 м/с. Модуль скорости мяча через 0,2 с после броска равен (м/с)
1. 2 2. 8,3 3. 8,7 4. 9,2 5. 12,8
18.С вышки бросили камень в горизонтальном направлении. Через 2 с камень упал на землю на расстоянии 40 м от основания вышки. Конечная скорость камня равна (м/с)
1. 20 2. 28,3 3. 23 4. 40 5. 17,3
19.Тело брошено с высоты с горизонтальной скоростью 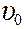
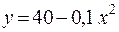
1. 40 2. 20 3. 5 4. 2,5 5. 1
20.Два бумажных диска (расстояние между ними 30 см), насаженные на общую горизонтальную ось, вращаются с угловой скоростью 2000 об/мин. Пуля, летящая горизонтально на расстоянии 12 см от оси, пробивает оба диска, причем пробоина во втором диске смещена по сравнению с первым на 6 см (по дуге окружности). Средняя скорость пули в промежутке между дисками равна (м)
1. 500 2. 250 3. 126 4. 105 5. 65
21.Материальная точка движется равноускоренно по окружности, лежащей в горизонтальной плоскости, по часовой стрелке. Вектор угловой скорости направлен
1. по касательной
2. вдоль радиуса окружности
3. вниз по оси вращения
4. вверх по оси вращения
5. среди ответов 1- 4 нет верного
22.Материальная точка движется равнозамедленно по горизонтальной окружности против часовой стрелки. Вектор углового ускорения направлен по
1. касательной к окружности
2. радиусу окружности
3. оси вращения вверх
4. оси вращения вниз
5. направлению угловой скорости
23.Материальная точка вращается в горизонтальной плоскости относительно неподвижной оси с угловым ускорением ε = 2t 2 . При t = 0, ω0 = 0. Закон изменения угловой скорости имеет вид
1. 
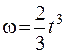
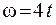

24.Точка вращается по окружности радиуса R согласно уравнению 
1. 
3. 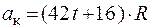
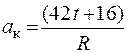
25.Точка вращается по окружности радиуса R согласно уравнению 
1. 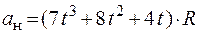
3. 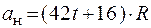
5.
26.Диск радиуса 10 см вращается согласно уравнению 
1. 3,54 2. 54,2 3. 2,4 4. 67,6 5. 26
27.Закон изменения угла поворота 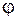

1. 19; 56 2. 56; 46 3. 88; 56 4. 86; 19 5. 76; 29
28.Закон изменения угловой скорости материальной точки имеет вид 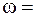
1. 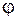
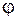
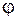
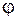
29.Маховик, вращавшийся с угловой скоростью 
1. 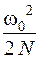
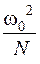

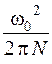
30.Шкив с радиусом R вращается под действием груза, подвешенного на нити. Ускорение груза а. В момент, когда груз прошел расстояние S, полное ускорение произвольной точки на ободе шкива определяется выражением
1. 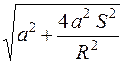
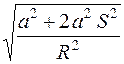
4. 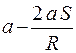
Видео:Физика - движение по окружностиСкачать

Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Видео:Задачи на движение. Учимся решать задачи на движение. Способы решения задач на движение.Скачать

Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Видео:#3.1 Движение по окружности. Центростремительное ускорение.Скачать

Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
🎥 Видео
Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Задача 1.1. КИНЕМАТИКА | Учимся решать задачи по физике с нуляСкачать

ФИЗИКА ОГЭ 2024 ВАРИАНТ 4 КАМЗЕЕВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать

УЧИМСЯ ЛЕГКО РЕШАТЬ ЗАДАЧИ НА ДВИЖЕНИЕ / ПОДСКАЗКА ВСЕГДА ПОД РУКОЙ СКОРОСТЬ ВРЕМЯ РАССТОЯНИЕСкачать

ВСЯ ФИЗИКА 7 КЛАСС ЗА 15 МИНУТ I Физика ОГЭ ЕГЭ 2024 I Эмиль Исмаилов - Global_EEСкачать

Вся программа 9 класса за ~50 минут | Физика 9 класс | Азат АдеевСкачать

Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Насколько хорошо ты знаешь физику? #global_ee #егэфизика #огэфизикаСкачать

Задача на среднюю скоростьСкачать

ОГЭ по математике. Вторая часть - 21-е заданияСкачать

№ 11.10. Задачи на движение повышенной сложности (4, 5 классы)Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Задача на логику как отмерить 4 литра воды, которую решит не каждыйСкачать