Геометрия | 5 — 9 классы
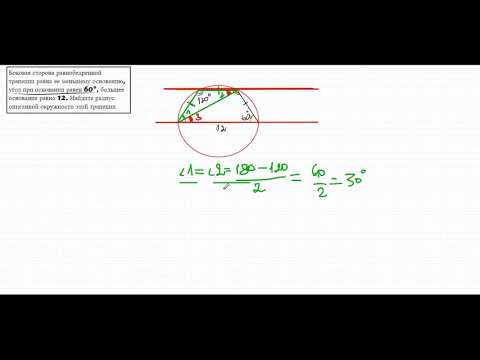
Большее основание трапеции является диаметром окружности радиуса корень из 2 — корень из 3, а меньшее является хордой, стягивающей дугу в 120 градусов этой окружности.
Найдите площадь трапеции.
Строим рисунок, смотрим угол между радиусом и хордой.
Если хорда стягивает дугу в 120 градусов, значит она равна радиусу окружности, умноженному на корень из 3.
Расстояние от хорды до диаметра есть радиус уможенный на 0.
5, получаем высоту.
В итоге получаем :
площадь = высота * (Диаметр + хорда) / 2, где
диаметр = 2 * радиус
хорда = (корень из 3) * радиус
подставляем все, получаем ответ :
( (радиус в квадрате) * (2 + корень из 3) ) / 4.
- Хорда окружности равна 3 корень из 3 см и стягивает дугу в 120 градусов?
- В равнобокую трапецию вписана окружность радиуса r?
- 1)Радиус окружности, вписанной в правильный треугольник, равен √3см?
- Если в окружности радиуса 9V3 проведена хорда, которая стягивает дугу в 60 градусов, то расстояние от центра окружности до хорды равно?
- Хорда окружности, равная12корней из 2 см, стягивает дугу в 90градусов?
- Хорда окружности равна 3 корень из 3 (см) и стягивает дугу в 120 градусов?
- Найдите радиус окружности, описанной около трапеции, если известно, что средняя линия трапеции равна 14 см, боковая сторона трапеции равна см, а одно из оснований является диаметром этой окружности?
- Хорда длиной 4 корень 2 см стягивает дугу 90 градусов?
- Трапеция вписана в окружность, её большее основание является диаметром этой окружности?
- Хорда окружности, равная m, стягивает дугу в 120°?
- Практикум «Решение геометрических задач второй части ОГЭ. Приёмы, способствующие решению геометрических задач».
- Подготовка к ОГЭ математика 9 практикум учитель математики:
- Нет царского пути в геометрии»
- Метод ключевой задачи Ключевая задача:
- Задача1 Из точки В к окружности проведены касательные
- Задача 2 В параллелограмме одна из диагоналей перпендикулярна боковой стороне
- Задача 3 Окружность вписана в ромб
- Задача 4 Найдите площадь равнобедренной трапеции, если её основания равны 14 и 50, а диагональ перпендикулярна боковой стороне
- Задача 5 B C A H O D Большее основание трапеции является диаметром описанной окружности
- Задача 6 B M C D H A 64 36 Равнобедренная трапеция с основаниями 64 и 36 описана около окружности
- ГИА-9 Ларин 2014, Вариант1, часть 2 №24
- ГИА-9 Ларин 2014, Вариант1, часть 2 №25
- ГИА-9 Ларин 2014, Вариант1, часть 2 №26
- Трапеция. Формулы, признаки и свойства трапеции
- Основные свойства трапеции
- Сторона трапеции
- Формулы определения длин сторон трапеции:
- Средняя линия трапеции
- Формулы определения длины средней линии трапеции:
- Высота трапеции
- Формулы определения длины высоты трапеции:
- Диагонали трапеции
- Формулы определения длины диагоналей трапеции:
- Площадь трапеции
- Формулы определения площади трапеции:
- Периметр трапеции
- Формула определения периметра трапеции:
- Окружность описанная вокруг трапеции
- Формула определения радиуса описанной вокруг трапеции окружности:
- Окружность вписанная в трапецию
- Формула определения радиуса вписанной в трапецию окружности
- Другие отрезки разносторонней трапеции
- Формулы определения длин отрезков проходящих через трапецию:
Видео:8 класс, 6 урок, ТрапецияСкачать

Хорда окружности равна 3 корень из 3 см и стягивает дугу в 120 градусов?
Хорда окружности равна 3 корень из 3 см и стягивает дугу в 120 градусов.
Найдите длину окружности и длину дуги.
Видео:Задача про трапецию, описанную около окружностиСкачать

В равнобокую трапецию вписана окружность радиуса r?
В равнобокую трапецию вписана окружность радиуса r.
Найдите площадь трапеции, если ее большое основание в 2 раза длиннее меньшего основания.
Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

1)Радиус окружности, вписанной в правильный треугольник, равен √3см?
1)Радиус окружности, вписанной в правильный треугольник, равен √3см.
Найдите периметр и площадь треугольника.
2)Хорда окружности, равная а, стягивает дугу в 90 градусов.
Найдите радиус окружности.
Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

Если в окружности радиуса 9V3 проведена хорда, которая стягивает дугу в 60 градусов, то расстояние от центра окружности до хорды равно?
Если в окружности радиуса 9V3 проведена хорда, которая стягивает дугу в 60 градусов, то расстояние от центра окружности до хорды равно.
V — квадратный корень.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Хорда окружности, равная12корней из 2 см, стягивает дугу в 90градусов?
Хорда окружности, равная12корней из 2 см, стягивает дугу в 90градусов.
Найдите радиус окружности.
Видео:Трапеция в окружности. Задача Шаталова.Скачать
Хорда окружности равна 3 корень из 3 (см) и стягивает дугу в 120 градусов?
Хорда окружности равна 3 корень из 3 (см) и стягивает дугу в 120 градусов.
Найдите длину окружности и длину дуги.
Видео:Найти среднюю линию трапеции, зная большее основаниеСкачать

Найдите радиус окружности, описанной около трапеции, если известно, что средняя линия трапеции равна 14 см, боковая сторона трапеции равна см, а одно из оснований является диаметром этой окружности?
Найдите радиус окружности, описанной около трапеции, если известно, что средняя линия трапеции равна 14 см, боковая сторона трапеции равна см, а одно из оснований является диаметром этой окружности.
Видео:Геометрия Центр окружности, описанной около равнобокой трапеции, принадлежит ее большему основаниюСкачать

Хорда длиной 4 корень 2 см стягивает дугу 90 градусов?
Хорда длиной 4 корень 2 см стягивает дугу 90 градусов.
Найдите длинну окружности.
Видео:Где центр окружности? ТрапецияСкачать

Трапеция вписана в окружность, её большее основание является диаметром этой окружности?
Трапеция вписана в окружность, её большее основание является диаметром этой окружности.
Средняя линия трапеции равна 16 см, высота равна 12 см.
Найдите радиус окружности.
Видео:Геометрия Около окружности с диаметром 15 см описана равнобедренная трапеция с боковой сторонойСкачать

Хорда окружности, равная m, стягивает дугу в 120°?
Хорда окружности, равная m, стягивает дугу в 120°.
Найдите радиус окружности.
На этой странице сайта вы найдете ответы на вопрос Большее основание трапеции является диаметром окружности радиуса корень из 2 — корень из 3, а меньшее является хордой, стягивающей дугу в 120 градусов этой окружности?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.
AB = BC⇒ΔABC — равнобедренный D — середина АС⇒BD — медиана, высота и биссектриса⇒ BD_|_AC⇒.
Task / 25874842 — — — — — — — — — — — — — — — — — — — ∠ABC _ вписанный угол Вписанный угол измеряется половинойдуги, на которую он опирается. ∠ABC = дуга(ADC) / 2⇒дуга(ADC) = 2 * 140° = 280°. Дуга(ABC) = 360° — дуга(ADC) = 360° — 280° = 80°. ∠ADC ..
Катет, лежащий против угла в 30 градусов равен половине гипотенузы.
Катет равен половине гипотенузе.
Вот наверное. НАсчет второго не уверен.
А, д, з, в вот ета без правлем.
Теорема — определение, требующее последующее доказательство. Аксиома — теорема, принимающаяся без доказатества. Планиметрия — раздел геометрии, изучающий фигуры на плоскости. Основными неопределяемыми понятиями в планиметрии являются точка и пряма..
Вроде так. Но я не сильно расписывала.
1м = 100см S = 24 * 100 = 2400см.
Окружность — линия с одинаком растоянием от середины. Центр — середина окружности. Радиус — растояние от центра до любой тлчки. Диаметр — растояние от одной точки окружности до другой(обязательно проходит через центр).
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Практикум «Решение геометрических задач второй части ОГЭ. Приёмы, способствующие решению геометрических задач».
Видео:Геометрия Точка касания окружности, вписанной в прямоугольную трапецию, делит ее большее основаниеСкачать

Подготовка к ОГЭ математика 9 практикум учитель математики:
Подготовка к ОГЭ математика 9 практикум
учитель математики: Зотова Рита Ямилевна
МБОУ СОШ №12
с углублённым изучением отдельных предметов
Видео:Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать

Нет царского пути в геометрии»
«Нет царского пути в геометрии»
Эвклид
Решение практических задач ОГЭ.
Приемы,
способствующие решению
геометрических задач.
Видео:Трапеция вписана в окружность. Найти радиус окружностиСкачать
Метод ключевой задачи Ключевая задача:
Метод ключевой задачи
Ключевая задача:
В прямоугольном треугольнике высота, проведённая к гипотенузе,
делит её на отрезки 18 и 32. Найти высоту.
Решение:
Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Задача1 Из точки В к окружности проведены касательные
Из точки В к окружности проведены касательные BP и BQ
(P и Q – точки касания).
Найти длину хорды PQ, если длина отрезка PB= 40,
а расстояние от центра окружности до хорды PQ равна 18.
1)PQ = 2PM; ∆ OPB – прямоугольный,
PM – высота.
2)Пусть BM = x, x > 0, тогда
Видео:Геометрия В окружность радиуса R вписана трапеция, у которой нижнее основание вдвое больше каждой изСкачать

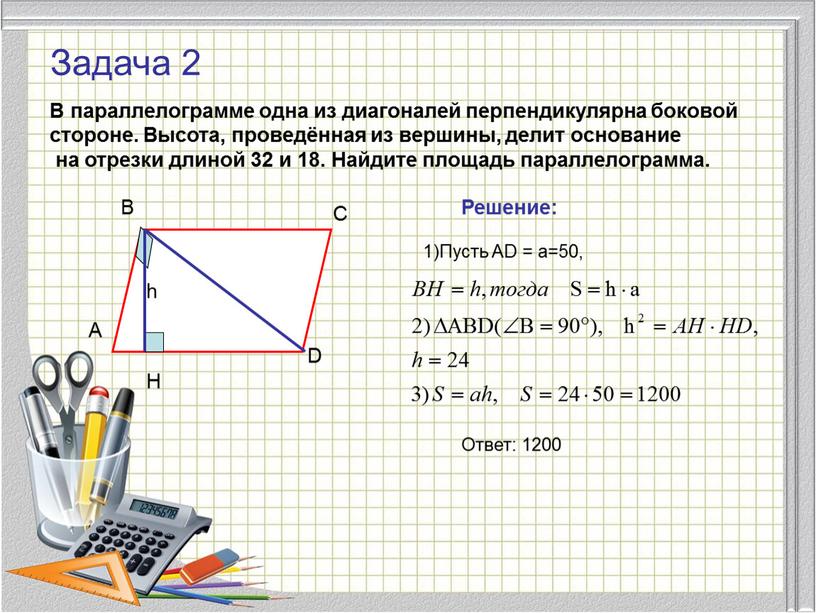
Задача 2 В параллелограмме одна из диагоналей перпендикулярна боковой стороне
В параллелограмме одна из диагоналей перпендикулярна боковой
стороне. Высота, проведённая из вершины, делит основание
на отрезки длиной 32 и 18. Найдите площадь параллелограмма.
Видео:Найти меньшее основание трапеции, зная большее основание, боковую сторона и синус острого углаСкачать

Задача 3 Окружность вписана в ромб
Окружность вписана в ромб. Радиус, проведённый из центра окружности
к стороне ромба, делит её на отрезки 18 и 24. Найдите радиус
вписанной окружности.
Радиус вписанной в ромб окружности
есть высота прямоугольного треугольника OAB,
Видео:Задание 16. Поиск большего основания трапецииСкачать

Задача 4 Найдите площадь равнобедренной трапеции, если её основания равны 14 и 50, а диагональ перпендикулярна боковой стороне
Найдите площадь равнобедренной трапеции, если её основания равны
14 и 50, а диагональ перпендикулярна боковой стороне.
Видео:Задание 26_Равнобедренная трапеция. Вписанная окружность.Скачать
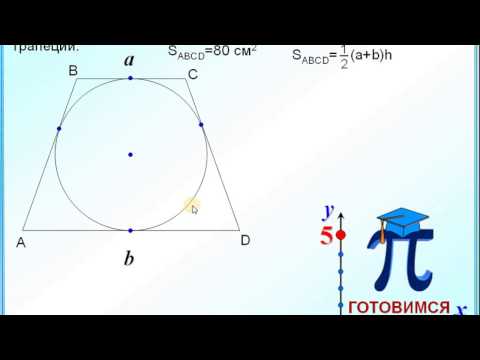
Задача 5 B C A H O D Большее основание трапеции является диаметром описанной окружности
Большее основание трапеции является диаметром описанной окружности.
Определите высоту трапеции, если её диагональ равна 40,
а меньшей из отрезков, на которые делит основание высота, равен 18.
1)Описать окружность можно только около равнобедренной трапеции.
2)∆ABC – прямоугольный (
B – вписанный, опирается на диаметр).
3)
Видео:Малоизвестные свойства равнобедренной трапеции. Разбор задачи 17 ЕГЭ профиль.Скачать
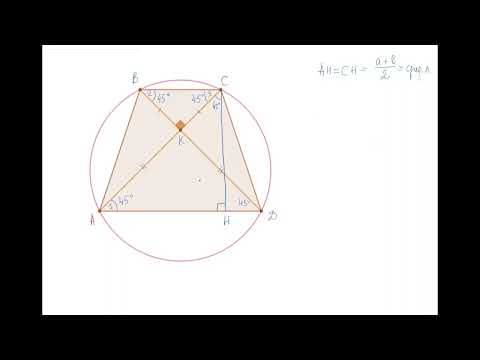
Задача 6 B M C D H A 64 36 Равнобедренная трапеция с основаниями 64 и 36 описана около окружности
Равнобедренная трапеция с основаниями 64 и 36 описана около
окружности. Найдите радиус окружности.
1)BM = BH (как отрезки касательных, проведённых из одной точки)
2) O – точка пересечения биссектрис
3) т.к. ABCD – описана около окружности,
то
BC + AD = AB + CD, AB = CD,
2AB = 36 + 64, AB = 50
4) т.к. BM = BH и BM = BC,
т.к. трапеция равнобедренная, то BM = 18 = BH
AH = 50-18=32
5) OH= r =
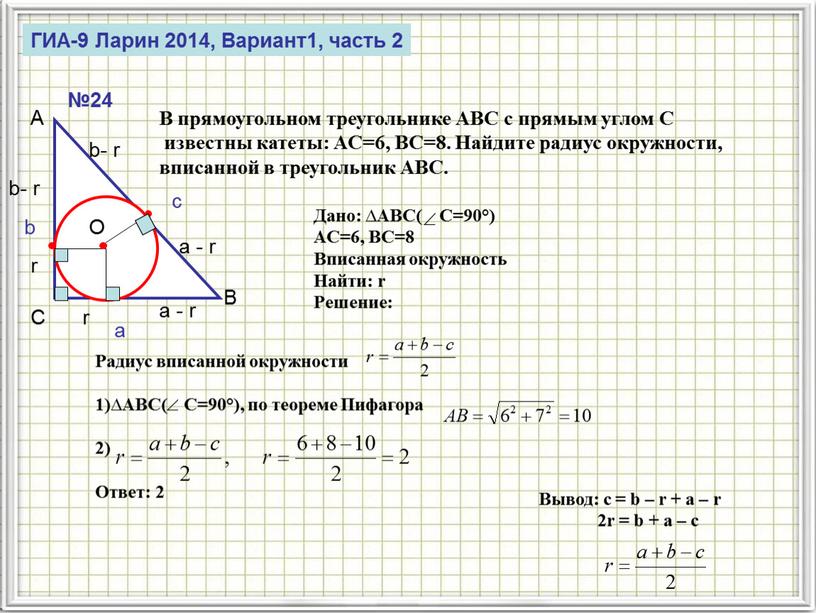
ГИА-9 Ларин 2014, Вариант1, часть 2 №24
ГИА-9 Ларин 2014, Вариант1, часть 2
В прямоугольном треугольнике ABC с прямым углом С
известны катеты: AC=6, BC=8. Найдите радиус окружности,
вписанной в треугольник ABC.
Дано: ∆ABC( С=90°)
AC=6, BC=8
Вписанная окружность
Найти: r
Решение:
Радиус вписанной окружности
1)∆ABC( С=90°), по теореме Пифагора
Вывод: c = b – r + a – r
2r = b + a – c
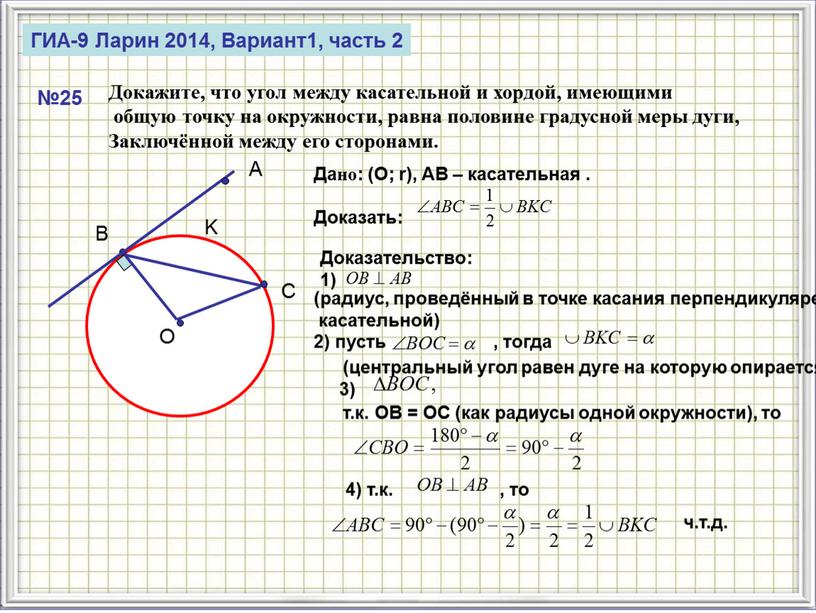
ГИА-9 Ларин 2014, Вариант1, часть 2 №25
ГИА-9 Ларин 2014, Вариант1, часть 2
Докажите, что угол между касательной и хордой, имеющими
общую точку на окружности, равна половине градусной меры дуги,
Заключённой между его сторонами.
Дано: (O; r), AB – касательная .
(радиус, проведённый в точке касания перпендикулярен
касательной)
2) пусть
(центральный угол равен дуге на которую опирается)
3)
т.к. OB = OC (как радиусы одной окружности), то
ГИА-9 Ларин 2014, Вариант1, часть 2 №26
ГИА-9 Ларин 2014, Вариант1, часть 2
Трапеция ABCD с основаниями AD = 6, и BC = 4 и диагональю BD = 7
вписана в окружность. На окружности взята точка K, отличная от точки D
так, что BK = 7. Найти длину отрезка AK.
Дано: ABCD – трапеция, описанная окружность,
BC = 4, AD = 6, BD = 7, BK = 7. K не совпадает с D.
Найти: AK
Решение:
Описать окружность можно только около равнобедренной
трапеции, поэтому BA = CD и
4) ∆ABK = ∆BCD (по стороне BD = BK и двум прилежащим к ней углам.
) из равенства треугольников следует, что BC = AK = 4.
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
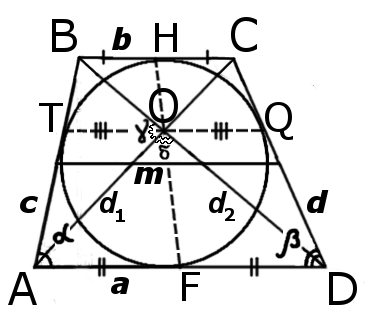 | 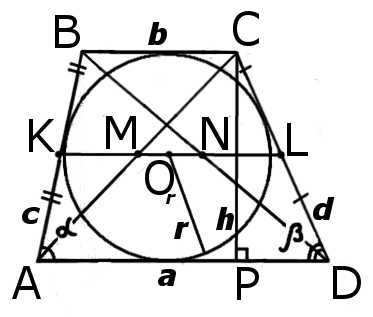 |
| Рис.1 | Рис.2 |
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
| m = | a + b |
| 2 |
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
| m = | a + b |
| 2 |
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
| h = | 2S |
| a + b |
5. Формула высоты трапеции через площадь и длину средней линии:
| h = | S |
| m |
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) | a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
| S = | ( a + b ) | · h |
| 2 |
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
| p = | a + c + d 1 |
| 2 |
a — большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.