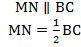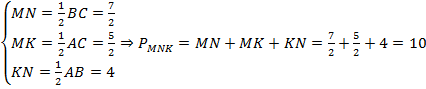Большая средняя линия прямоугольного треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:8 класс, 25 урок, Средняя линия треугольникаСкачать

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

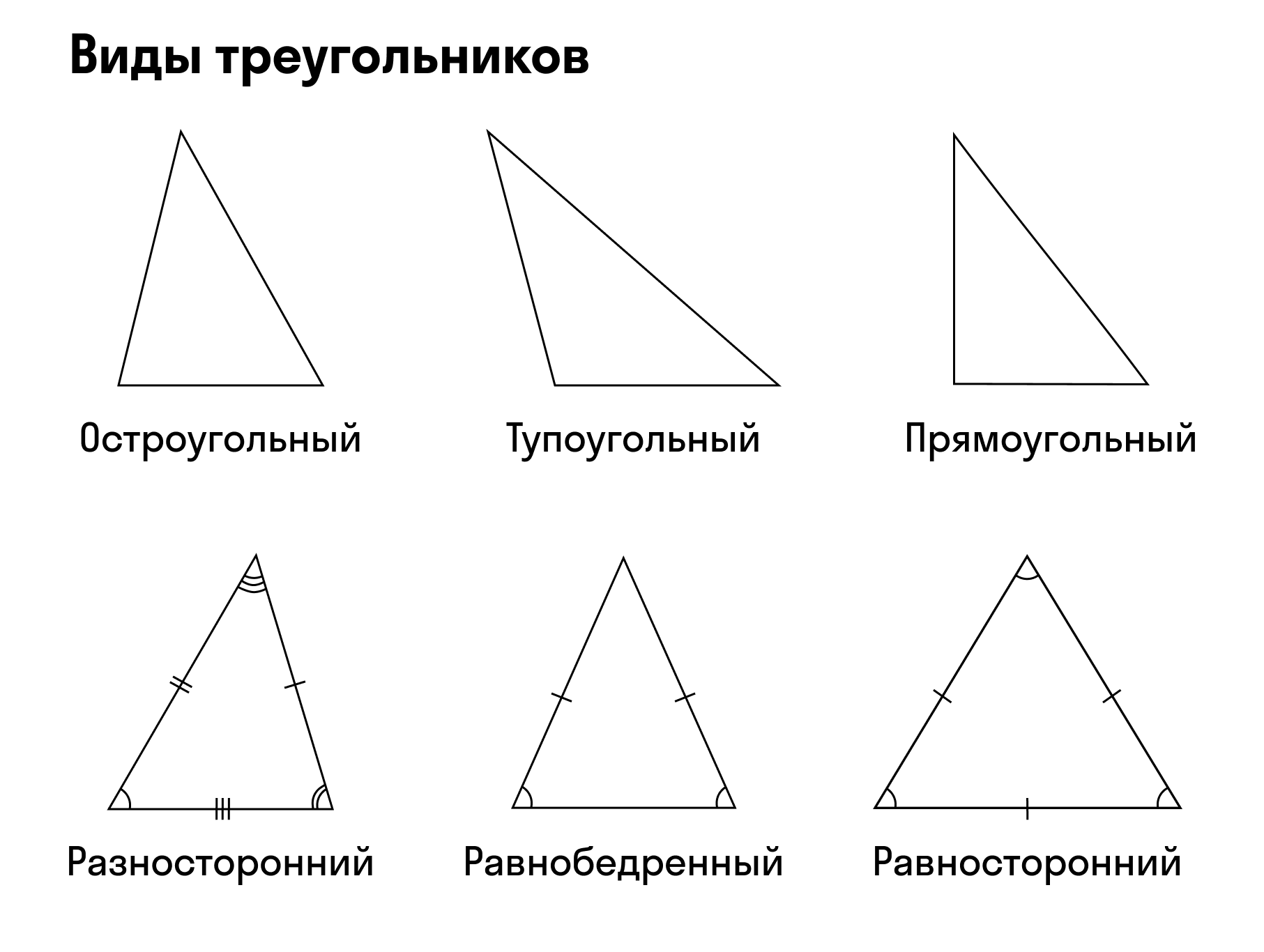
• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

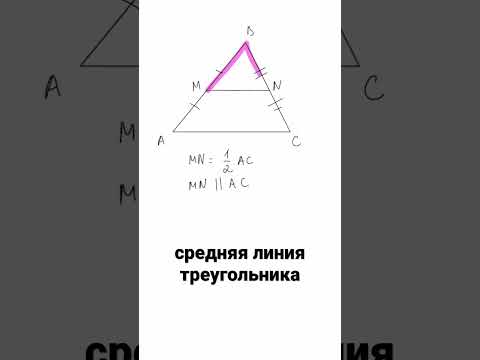
​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Видео:Средняя линия треугольникаСкачать

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Видео:64. Средняя линия треугольникаСкачать

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

1. Средняя линия равна половине длины основания и параллельна ему.
2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

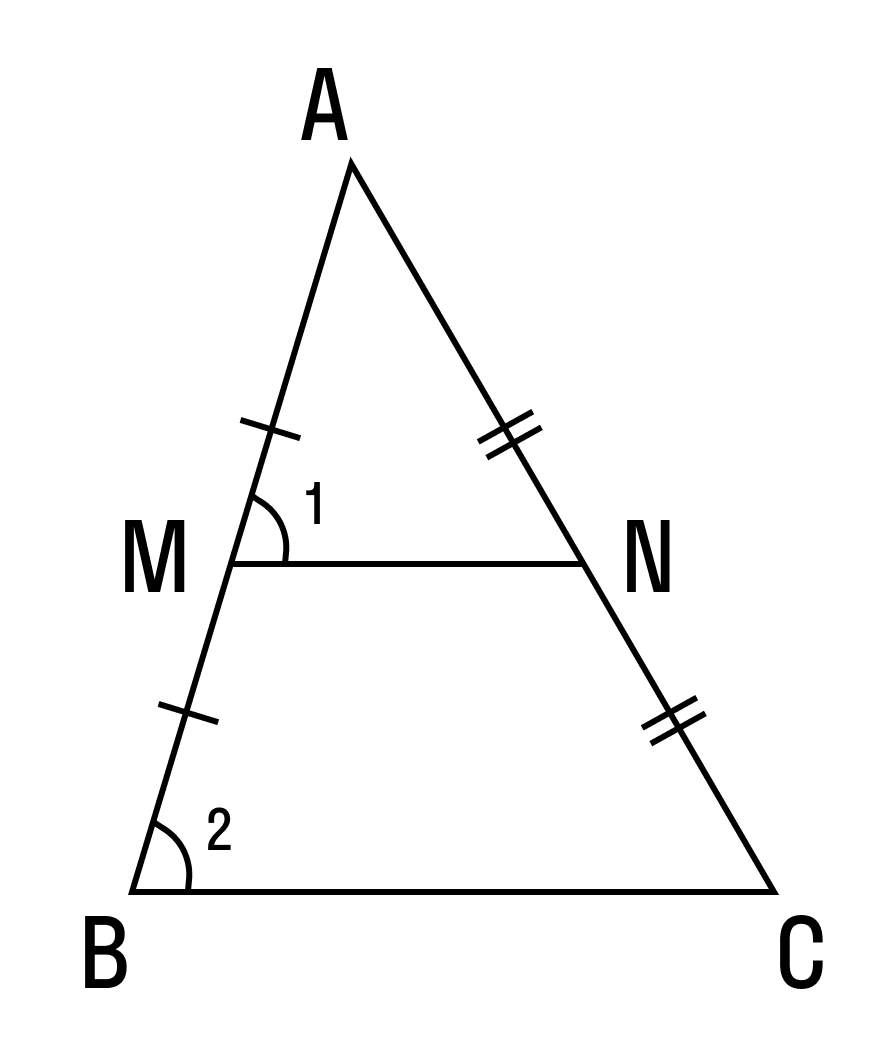
По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.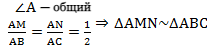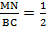

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

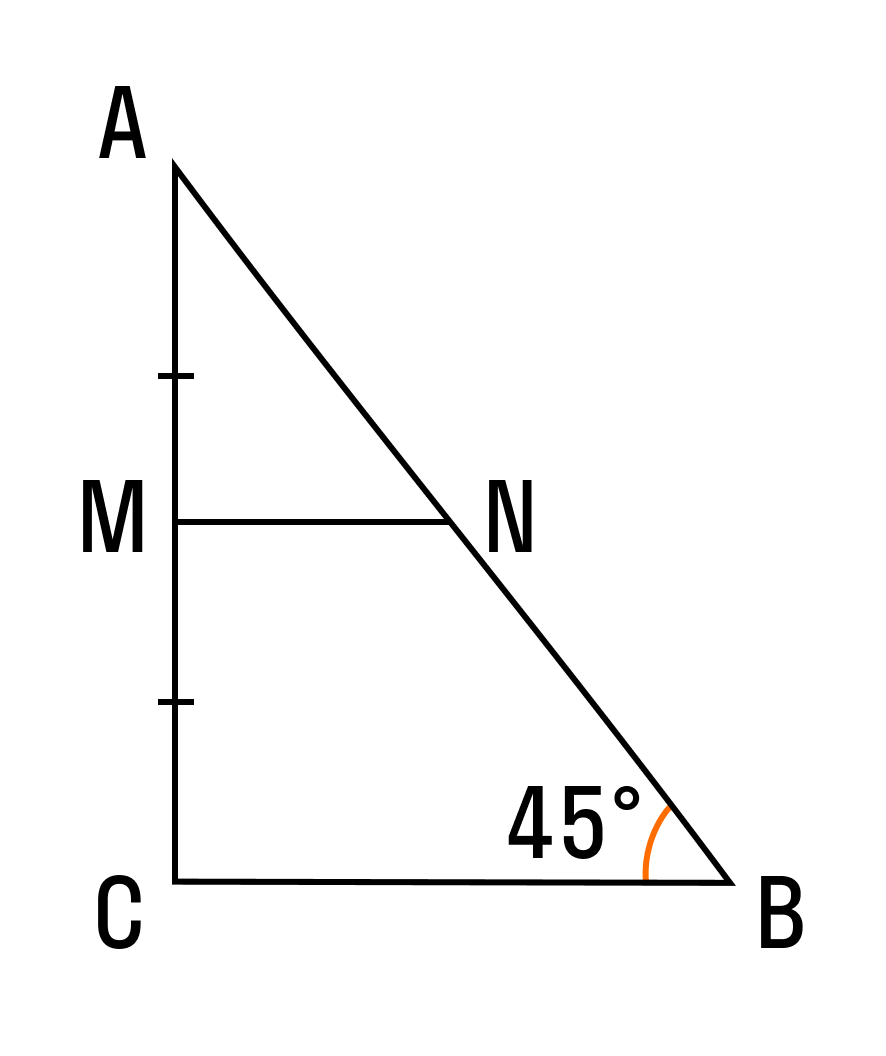
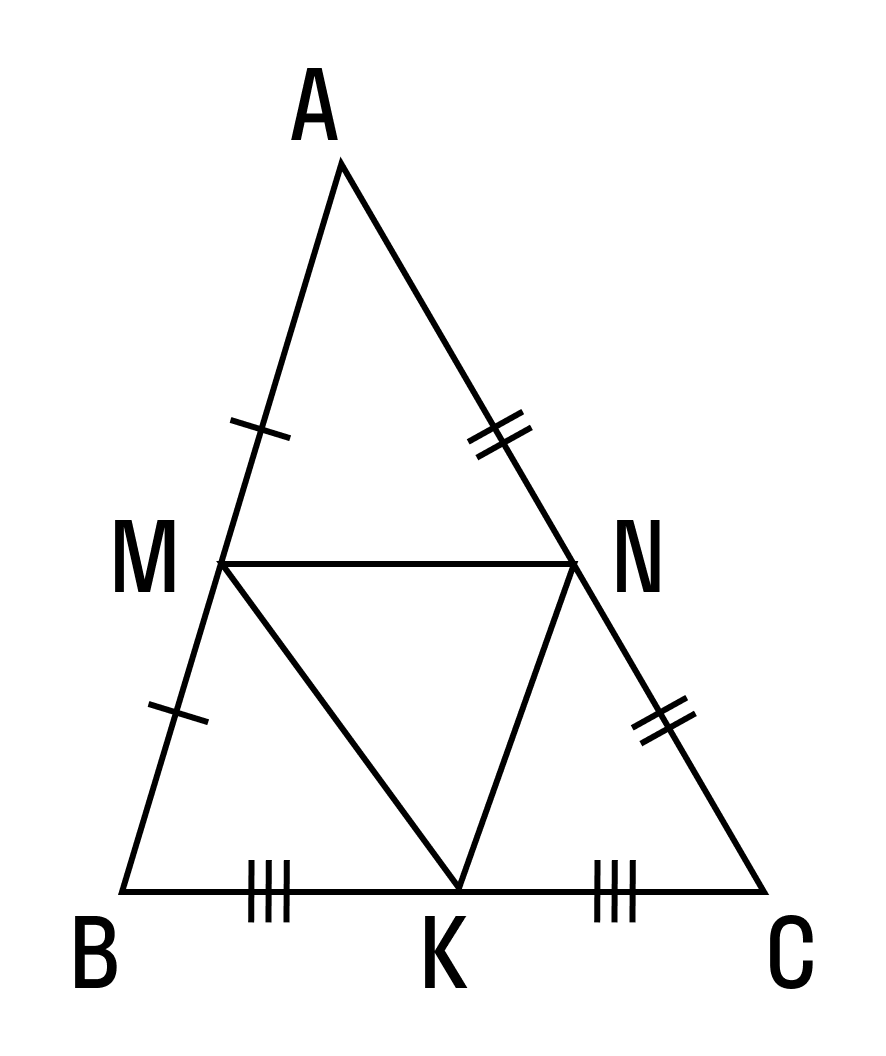
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Видео:МАТЕМАТИКА | Средняя линия треугольникаСкачать

Средняя линия прямоугольного треугольника

Средняя оценка: 4.2

Всего получено оценок: 61.

Средняя оценка: 4.2

Всего получено оценок: 61.

Прямоугольный треугольник стоит особняком от остальных треугольников. Прямой угол делает возможным применение других признаков равенства и подобия. Для углов в прямоугольном треугольнике можно без дополнительных построений использовать геометрические тождества, а любую из сторон можно найти по теореме Пифагора. Но среднюю линию прямоугольного треугольника определить трудно просто потому, что она редко упоминается в задачах, из-за чего мало кто может себе её визуально представить.

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Что такое средняя линия прямоугольного треугольника?

Средняя линия – это отрезок, соединяющий середины сторон в треугольнике. В любом треугольнике можно провести три средних линии. При этом этот отрезок будет равен половине основания – это и считается формулой средней линии прямоугольного треугольника. Основанием считается сторона, с которой средняя линия не пересекается.

Причем, если средняя линия проводится в прямоугольном треугольнике, то каждый из четырех получившихся треугольников будет являться прямоугольным.

Все эти свойства можно использовать в ряде задач, что позволяет создавать интересные уникальные решения и доказательства.

Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

Задача 1

В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. При этом MN=NP=2.

Рис. 1. Рисунок к задаче

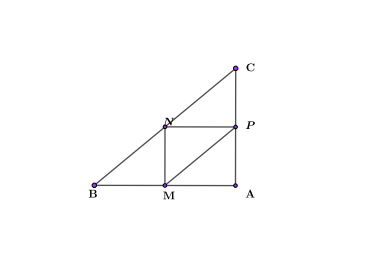
В центре треугольника средними линиями образован малый прямоугольный треугольник, катеты которого известны. Тогда его площадь равна: $S=<1over>*MN*NP=<1over>*2*2=2$.

Так как все 4 малых треугольника равны, то площадь большого будет равна: $S=4*2=8$

Видео:Решение прямоугольных треугольниковСкачать

Задача 2

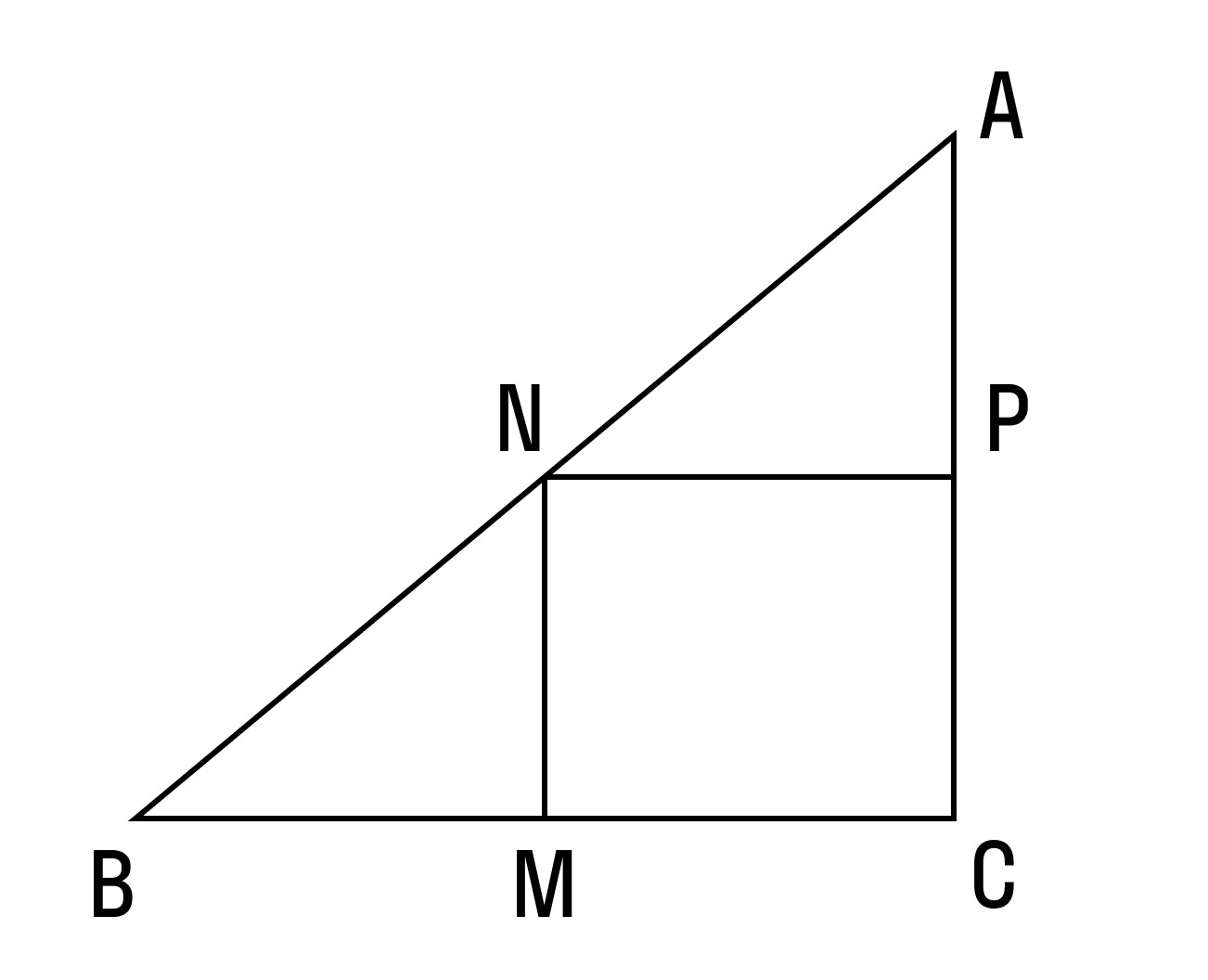
В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. В получившемся прямоугольнике MNPA известно, что диагональ MP равна 5, а синус угла между диагоналями равен 0,48. Найти площадь большого прямоугольного треугольника.

Рис. 2. Рисунок к задаче

В прямоугольнике две диагонали между собой равны. Одна из диагоналей MP = 5, значит и вторая диагональ AN равна тоже 5.

Найдем площадь прямоугольника, как произведение диагоналей на синус угла между ними.

В большом треугольнике 4 малых, а в прямоугольнике 2 малых треугольника. Все малые треугольники между собой равны, значит, чтобы найти площадь прямоугольного треугольника, нужно умножить площадь прямоугольника на 2.

$S=12*2=24$ – ответ получен.

Видео:Средняя линия треугольника. Видеоурок 13. Геометрия 8 класс.Скачать

Задача 3

В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. Найти площадь прямоугольника MNPA, если известно, что площадь АВС равна 36.

Рис. 3. Рисунок к задаче

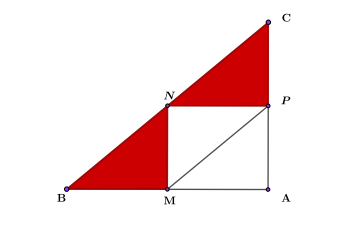
Аналогично с предыдущей задачей, можно вывести утверждение, что площадь треугольника равна двум площадям малого прямоугольника. Подставим в выражение цифры и выразим неизвестное. Площадь треугольника обозначим за S, прямоугольника s.

Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Что мы узнали?

Мы узнали, что такое средняя линия, поговорили о свойствах средней линии и выделили особенности средней линии в прямоугольном треугольнике. Также мы закрепили пройденный материал, подробно изучив алгоритм решения задач на заданную тему.

Видео:Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Средняя линия прямоугольного треугольника – формула

Средняя линия прямоугольного треугольника – это прекрасная возможность для составителей задач. Большая часть обучающихся знают, что такое средняя линия и умело используют ее свойства в решении. Но как только этот отрезок появляется на чертеже прямоугольного треугольника, то сразу впадают в ступор из-за некоторой необычности рисунка, поэтому разберемся в теме подробнее.

Видео:пропорциональные отрезки в ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ 8 классСкачать

Что такое прямоугольный треугольник?

В общем случае, треугольник это фигура, состоящая из стрех сторон и трех углов. В зависимости от величин углов, входящих в состав треугольника выделяют:

• Остроугольные треугольники, все углы которых меньше 90 градусов.
• Тупоугольные треугольники, один из углов которых больше 90 градусов.
• Прямоугольные треугольники, один из углов которых равен 90 градусам.

Прямоугольные треугольники интересны специальными формулами, которые значительно упрощают решение. Но средняя линия прямоугольного треугольника ни чем не отличается от средней линии произвольного. Почему задачи с этим отрезком вызывают затруднения?

Только из-за необычности чертежа

Рис. 1. Прямоугольный треугольник.

Видео:Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать

Средняя линия

Что такое средняя линия? Это один из характеризующих отрезков любого треугольника. Средняя линия соединяет середины смежных сторон многоугольника.

Средняя линия есть не только у треугольника. Она существует у каждой выпуклой фигуры. При этом свойства средних линий треугольников не всегда совпадают с свойствами средних линий трапеций. Поэтому будьте аккуратны, у каждой фигуры есть свои свойства и признаки.

Рис. 2. Средняя линия трапеции.

Видео:8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

Свойства средней линии

Свойств у средней линии не так много, но все они более чем интересны.

• Средняя линия всегда параллельна стороне, через которую она не проходит. Иначе говорят, что средняя линия параллельна основанию. Так проще запомнить это свойство, но немного страдает формулировка. Дело в том, что в любом треугольнике можно провести 3 средних линии, а основание только одно, поэтому будьте аккуратнее в формулировках.
• Средняя линия равна половине основания. А вернее не основания, а стороны, которую средняя линия не пересекает. Это и есть формула средней линии прямоугольного треугольника.
• Средняя линия отсекает треугольник подобный изначальном с коэффициентом подобия 1:2

Если формулировка «Средняя линия параллельна основанию» не совсем правильная, то почему же ее применяют в учебнике? Дело в том, что любое свойство должно быть коротким и ясным для простоты запоминания. Поэтому и сокращают некоторые высказывания. А основанием произвольного треугольника можно считать любую сторону, а значит неправильной формулировку назвать нельзя.

Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Задача

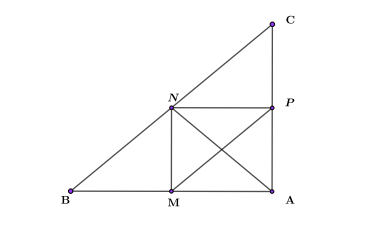
В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. В получившемся прямоугольнике MNPA известно, что синус угла между диагоналями равен 0,5. А средние линии MN и NP равны 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Рис. 3. Рисунок к задаче.

В прямоугольнике две диагонали между собой равны. Одна из диагоналей MP это гипотенуза прямоугольного треугольника MNP. Катеты треугольника известны, значит можно найти гипотенузу через теорему Пифагора.

Найдем площадь прямоугольника, как произведение диагоналей на синус угла между ними.

В большом треугольнике 4 малых, а в прямоугольнике 2 малых треугольника. Все малые треугольники между собой равны, значит, чтобы найти площадь прямоугольного треугольнику, нужно умножить площадь прямоугольника на 2.

$S=12,5*2=25$ – ответ получен.

Видео:Средняя линия треугольника | Геометрия 7-9 класс #62 | ИнфоурокСкачать

Что мы узнали?

Мы узнали, что такое средняя линия прямоугольного треугольника. Поговорили о свойствах средней линии и решили небольшую задачу для закрепления материала.

🔥 Видео

Высота в прямоугольном треугольнике. 8 класс.Скачать

Задание 25 Средняя линия треугольникаСкачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать