 Формула бинома Ньютона Формула бинома Ньютона |
 Связь бинома Ньютона с треугольником Паскаля Связь бинома Ньютона с треугольником Паскаля |
 Свойства биномиальных коэффициентов Свойства биномиальных коэффициентов |
- Формула бинома Ньютона
- Связь бинома Ньютона с треугольником Паскаля
- Свойства биномиальных коэффициентов
- Конспект на тему «Бином Ньютона. Треугольник Паскаля» (для студентов)
- Бином Ньютона
- Бином Ньютона — формула
- Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля
- Доказательство формулы бинома Ньютона
- 📹 Видео
Видео:Бином Ньютона и его свойства. 9 класс.Скачать

Формула бинома Ньютона
В Таблице 1 из раздела «Формулы сокращенного умножения» приведены формулы для натуральных степеней бинома
в случаях, когда n = 1, 2, 3, 4, 5, 6.
В настоящем разделе рассматривается общий случай этой формулы, т.е. случай произвольного натурального значения n .
Утверждение . Для любого натурального числа n и любых чисел x и y справедлива формула бинома Ньютона :
– числа сочетаний из n элементов по k элементов.
В формуле (1) слагаемые
называют членами разложения бинома Ньютона , а числа сочетаний 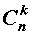
Если в формуле (1) заменить y на – y , то мы получим формулу для n — ой степени разности:
Видео:Треугольник ПаскаляСкачать

Связь бинома Ньютона с треугольником Паскаля
Напомним, что треугольник Паскаля имеет следующий вид:
| № | Треугольник Паскаля |
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| … | … |
Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:
| № | Треугольник Паскаля |
| 0 | 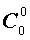 |
| 1 | 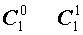 |
| 2 | 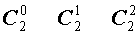 |
| 3 | 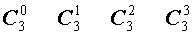 |
| 4 | 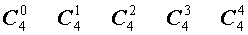 |
| 5 | 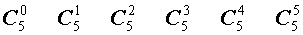 |
| 6 | 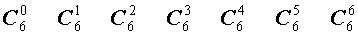 |
| … | … |
| Треугольник Паскаля |
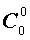 |
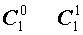 |
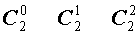 |
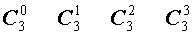 |
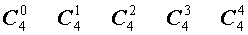 |
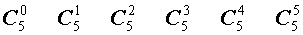 |
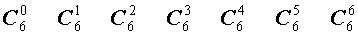 |
| … |
| Треугольник Паскаля |
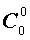 |
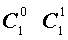 |
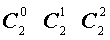 |
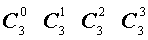 |
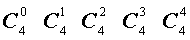 |
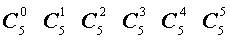 |
| … |
Видео:Бином Ньютона и треугольник Паскаля | Учитель года Москвы — 2020Скачать

Свойства биномиальных коэффициентов
Для биномиальных коэффициентов справедливы равенства:
| 1 | 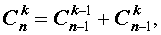 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Показатель степени | Биноминальные коэффициенты | ||||||||||
| 0 | C 0 0 | ||||||||||
| 1 | C 1 0 | C 1 1 | |||||||||
| 2 | C 2 0 | C 2 1 | C 2 2 | ||||||||
| 3 | C 3 0 | C 3 1 | C 3 2 | C 3 3 | |||||||
| ⋮ | … | … | … | … | … | … | … | … | … | ||
| n | C n 0 | C n 1 | … | … | … | … | … | C n n — 1 | C n n | ||
При натуральных n такой треугольник Паскаля состоит из значений коэффициентов бинома:
| Показатель степени | Биноминальные коэффициенты | ||||||||||||||
| 0 | 1 | ||||||||||||||
| 1 | 1 | 1 | |||||||||||||
| 2 | 1 | 2 | 1 | ||||||||||||
| 3 | 1 | 3 | 3 | 1 | |||||||||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||||||||
| ⋮ | … | … | … | … | … | … | … | … | … | … | … | … | … | ||
| n | C n 0 | C n 1 | … | … | … | … | … | … | … | … | … | C n n — 1 | C n n | ||
Боковые стороны треугольника имеют значение единиц. Внутри располагаются числа, которые получаются при сложении двух чисел соседних сторон. Значения, которые выделены красным, получают как сумму четверки, а синим – шестерки. Правило применимо для всех внутренних чисел, которые входят в состав треугольника. Свойства коэффициентов объясняются при помощи бинома Ньютона.
Видео:Треугольник ПаскаляСкачать

Доказательство формулы бинома Ньютона
Имеются равенства, которые справедливы для коэффициентов бинома Ньютона:
- коэффициента располагаются равноудалено от начала и конца, причем равны, что видно по формуле C n p = C n n — p , где р = 0 , 1 , 2 , … , n ;
- C n p = C n p + 1 = C n + 1 p + 1 ;
- биномиальные коэффициенты в сумме дают 2 в степени показателя степени бинома, то есть C n 0 + C n 1 + C n 2 + . . . + C n n = 2 n ;
- при четном расположении биноминальных коэффициентов их сумма равняется сумме биномиальных коэффициентов, расположенных в нечетных местах.
Равенство вида a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . . + C n n — 1 · a · b n — 1 + C n n · b n считается справедливым. Докажем его существование.
Для этого необходимо применить метод математической индукции.
Для доказательства необходимо выполнить несколько пунктов:
- Проверка справедливости разложения при n = 3 . Имеем, что
a + b 3 = a + b a + b a + b = a 2 + a b + b a + b 2 a + b = = a 2 + 2 a b + b 2 a + b = a 3 + 2 a 2 b + a b 2 + a 2 b + 2 a b + b 3 = = a 3 + 3 a 2 b + 3 a b 2 + b 3 = C 3 0 a 3 + C 3 1 a 2 b + C 3 2 a b 2 + C 3 3 b 3 - Если неравенство верно при n — 1 , тогда выражение вида a + b n — 1 = C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1
- Доказательство равенства a + b n — 1 = C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1 , основываясь на 2 пункте.
Доказательство 1
a + b n = a + b a + b n — 1 = = ( a + b ) C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1
Необходимо раскрыть скобки, тогда получим a + b n = C n — 1 0 · a n + C n — 1 1 · a n — 1 · b + C n — 1 2 · a n — 2 · b 2 + . . . + C n — 1 n — 2 · a 2 · b n — 2 + + C n — 1 n — 1 · a · b n — 1 + C n — 1 0 · a n — 1 · b + C n — 1 1 · a n — 2 · b 2 + C n — 1 2 · a n — 3 · b 3 + . . . + C n — 1 n — 2 · a · b n — 1 + C n — 1 n — 1 · b n
Производим группировку слагаемых
a + b n = = C n — 1 0 · a n + C n — 1 1 + C n — 1 0 · a n — 1 · b + C n — 1 2 + C n — 1 1 · a n — 2 · b 2 + . . . + + C n — 1 n — 1 + C n — 1 n — 2 · a · b n — 1 + C n — 1 n — 1 · b n
Имеем, что C n — 1 0 = 1 и C n 0 = 1 , тогда C n — 1 0 = C n 0 . Если C n — 1 n — 1 = 1 и C n n = 1 , тогда C n — 1 n — 1 = C n n . При применении свойства сочетаний C n p + C n p + 1 = C n + 1 p + 1 , получаем выражение вида
C n — 1 1 + C n — 1 0 = C n 1 C n — 1 2 + C n — 1 1 = C n 2 ⋮ C n — 1 n — 1 + C n — 1 n — 2 = C n n — 1
Произведем подстановку в полученное равенство. Получим, что
a + b n = = C n — 1 0 · a n + C n — 1 1 + C n — 1 0 · a n — 1 · b + C n — 1 2 + C n — 1 1 · a n — 2 · b 2 + . . . + + C n — 1 n — 1 + C n — 1 n — 2 · a · b n — 1 = C n — 1 n — 1 · b n
После чего можно переходить к биному Ньютона, тогда a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . . + C n n — 1 · a · b n — 1 + C n n · b n .
📹 Видео
✓ Бином Ньютона. Игра в слова. Числа сочетаний | Комбинаторика | Ботай со мной #057 | Борис ТрушинСкачать

Бином Ньютона и треугольник ПаскаляСкачать

ТРЕУГОЛЬНИК ПАСКАЛЯ 😊 ЧАСТЬ I #shorts #математика #егэ #задачи #задачаналогику #егэ2022 #огэ2022Скачать

Бином Ньютона максимально простым языкомСкачать

Применение формулы бинома Ньютона и треугольника ПаскаляСкачать

Бином Ньютона. 10 класс.Скачать

Зачем нужен треугольник Паскаля (спойлер: для формул сокращённого умножения)Скачать

Треугольник Паскаля Python. Коэффициенты для Бинома НьютонаСкачать

Бином Ньютона.Треугольник Паскаля.Скачать

Бином Ньютона. Практическая часть. 10 класс.Скачать

Урок 10. Бином Ньютона. Треугольник Паскаля. Алгебра 11 класс.Скачать

Бином Ньютона и треугольник ПаскаляСкачать


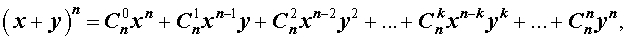
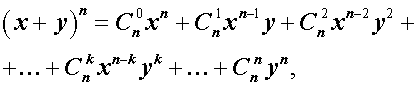
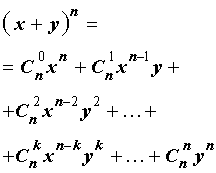
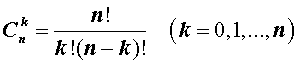
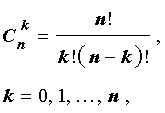
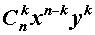
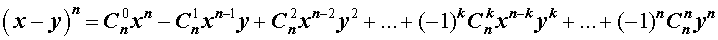
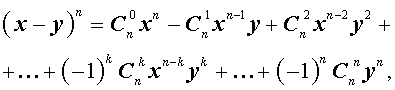
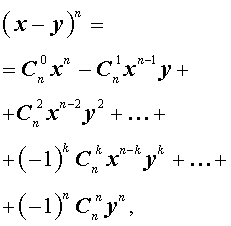
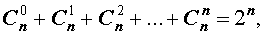
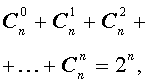
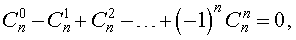
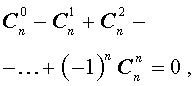
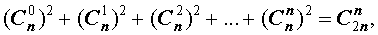
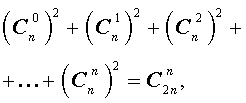
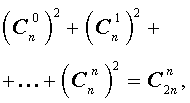
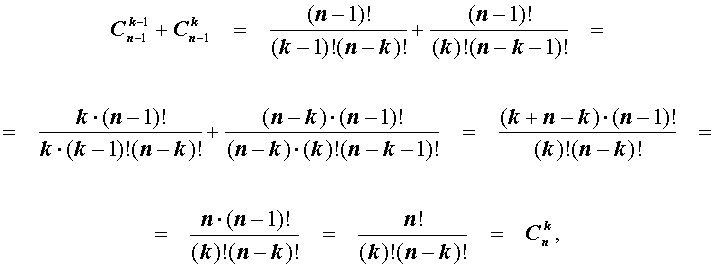
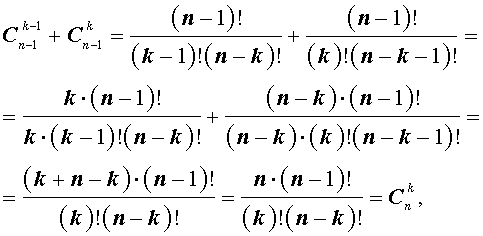
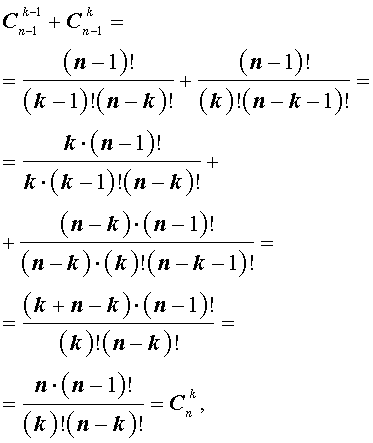
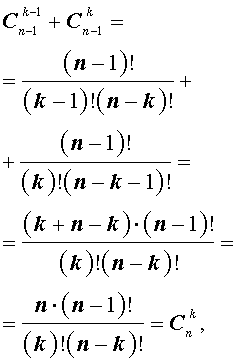
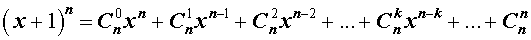
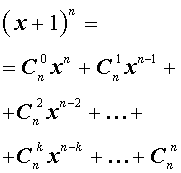
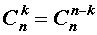
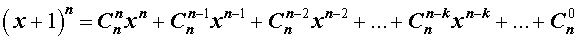
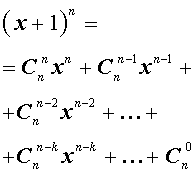
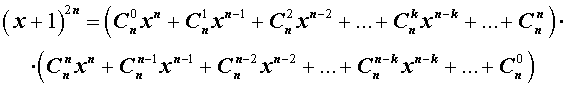
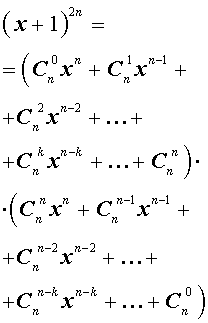

 в многочлен. Каждый из нас изучал наизусть формулы «квадрата суммы»
в многочлен. Каждый из нас изучал наизусть формулы «квадрата суммы»  и «куба суммы»
и «куба суммы»  , но при увеличении показателя степени с определением коэффициентов при членах многочлена начинаются трудности.
, но при увеличении показателя степени с определением коэффициентов при членах многочлена начинаются трудности.
 – называют биномиальными коэффициентами.
– называют биномиальными коэффициентами. – формула для числа сочетаний,
– формула для числа сочетаний,  .
. есть частный случай бинома Ньютона при n=2.
есть частный случай бинома Ньютона при n=2.
 и
и  с коэффициентами 1. Ясно также, что всякий иной член многочлена выглядит как произведение определённых степеней каждого из слагаемых двучлена
с коэффициентами 1. Ясно также, что всякий иной член многочлена выглядит как произведение определённых степеней каждого из слагаемых двучлена  ), причём сумма степеней всегда равна n.
), причём сумма степеней всегда равна n. сумма степеней сомножителей во всех членах равна трём (3, 2+1, 1+2, 3). То же самое справедливо и для любой другой степени. Вопрос лишь в том, какие коэффициенты следует ставить при членах.
сумма степеней сомножителей во всех членах равна трём (3, 2+1, 1+2, 3). То же самое справедливо и для любой другой степени. Вопрос лишь в том, какие коэффициенты следует ставить при членах.

