Бермудские треугольники в математике

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Треугольник с научной точки зрения

Что такое треугольник?

Треугольник в истории геометрии

Почему у треугольника три стороны?

Жестко ли спать на треугольнике?

Применение треугольников в быту

Треугольники в архитектуре

Загадки природы, связанные с треугольниками:

ПРАКТИЧЕСКАЯ ЧАСТЬ

Разнообразный мир треугольников или где в жизни встречается треугольник.

Введение

Геометрия – наука, занимающаяся изучением геометрических фигур. Одной из основных фигур, которую изучают в геометрии является — треугольник. Треугольник является важнейшей фигурой планиметрии, и потому в первую очередь изучают многочисленные свойства этой фигуры. Также треугольник является составной частью объемных фигур, а его свойства мы часто используем при решении различных задач. В жизни форма этой фигуры используется во многих областях. А также имеет свои тайны. (Бермудский треугольник, Египетские пирамиды)

Цели проекта:

Изучить понятие треугольника и его элементов и свойств.

Развить логическое мышление учащихся. Сформировать познавательный интерес к изучению геометрии.

Научиться устанавливать межпредметные связи математики с такими учебными предметами как история, литература, информатика, черчение.

Выяснить, что значит математика в жизни людей: является второстепенной наукой или математика – это неотъемлемая часть в жизни человечества.

Задачи проекта:

Изучить свойства треугольника;

Научиться устанавливать связи между различными геометрическими фигурами;

Развить пространственное и логическое мышление;

Рассмотреть взаимосвязь между математикой и жизнью;

Проанализировать, как жизнь зависит от математики;

Гипотеза:

Можно ли обойтись без треугольника в жизни и в математике?

Если математика – второстепенная наука, то законы, которые она изучает знать простому человеку совсем не обязательно, то есть эти законы в обыденной жизни никому не нужны.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Что такое треугольник?

Ты на меня, ты на него, На всех нас посмотри. У нас всего, у нас всего У нас всего по три. Три стороны и три угла, И столько же вершин. И трижды трудные дела Мы трижды совершим

Треугольник (в евклидовом пространстве) — это геометрическая фигура, которая образована тремя отрезками, соединяющие три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла. Если три точки лежат на одной прямой, то «треугольник» с вершинами в трёх данных точках называется вырожденным. Все остальные треугольники невырожденные.

В неевклидовых пространствах в качестве сторон треугольника выступают геодезические линии, которые, как правило, являются криволинейными. Поэтому такие треугольники называют криволинейными.

Важным частным случаем неевклидовых треугольников являются сферические треугольники.

Треугольник — это часть плоскости, ограниченная минимально возможным количеством сторон. Любой многоугольник можно точно разбить на треугольники, лишь связав его вершины отрезками, не пересекающими его стороны. С некоторым приближением, на треугольники можно разбить поверхность любой формы, как на плоскости, так и в пространстве. Так как треугольник — это многоугольник, ограниченный минимально возможным количеством сторон, то при его разбиении на треугольники процесс решений задач будет намного легче чем решения огромным многоугольников. Разбиение геометрического объекта (в данном случае это разбиение на треугольники) называется триангуляция.[1]

Треугольник в истории геометрии.

Треугольник – это простейшая плоская фигура, но можно сказать, что вся (или почти вся) геометрия со времен «Начал» Евклида покоится на «трёх китах» – трёх признаках равенства треугольников.

За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о «геометрии треугольника» как о самостоятельном разделе элементарной геометрии.

Геометрия, по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве. Этот процесс привёл, наконец, к качественному скачку. Геометрия превратилась в самостоятельную математическую науку: появились систематические её изложения, где её предложения последовательно доказывались.

1.3.Почему у треугольника три стороны?

Мы знакомы с разными многоугольниками: треугольник, четырехугольник, пятиугольник и т.д. Почему же именно треугольник считают символом геометрии?

Оказывается, потому, что треугольник – это многоугольник с наименьшим количеством сторон. Действительно, попробуйте построить многоугольник с двумя сторонами и у вас ничего не получится, ведь для того чтобы получился многоугольник нужна третья сторона.[5]

Жестко ли спать на треугольнике?

Вот такой шуточный вопрос возникает тогда, когда мы знакомимся с таким понятием, как жесткость треугольника.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Из третьего признака равенства треугольников следует, что треугольник — жёсткая фигура. Поясню, что это означает. Представим себе две рейки, у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой: сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек. Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.

Рассмотрим модели двух фигур — треугольника и четырёхугольника и выясним, можно ли, не меняя длины сторон, изменить форму фигуры? Под действием небольшой силы четырёхугольник изменил свою форму, а треугольник нет.

Можно сказать, что треугольник – не изменяющаяся фигура. В нем нельзя сдвинуть или раздвинуть никакие две стороны, в отличие от любого другого многоугольника. В треугольнике нельзя изменить ни один из углов. Таким образом, треугольник – жесткая фигура.[6]

Великий ученый Фалес Милетский основал одну из прекраснейших наук – геометрию. Он имел титул одного из семи мудрецов Греции, он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции VI век до нашей эры

Средние века немного дали геометрии, и следующим великим событием в её истории стало открытие Декартом в XVII веке координатного метода («Рассуждение о методе», 1637). Точкам сопоставляются наборы чисел, это позволяет изучать отношения между формами методами алгебры. Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями. Примерно одновременно с этим Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии. Метод координат лежит в основе, появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями.[2]

1.4. Треугольники в архитектуре

Треугольники повсюду встречаются в нашей жизни: в костюмах, в бытовых приборах, а также в архитектуре.

Треугольник Пенроуза — одна из основных невозможных фигур, известная также под названиями невозможный треугольник и трибар.

Был открыт в 1934 году шведским художником Оскаром Реутерсвардом, который изобразил его в виде набора кубиков. В 1980 году этот вариант невозможного треугольника был напечатан на шведских почтовых марках.

Широкую известность эта фигура обрела после опубликования статьи о невозможных фигурах в Британском журнале психологии английским математиком Роджером Пенроузом в 1958 году. В этой статье невозможный треугольник был изображен в наиболее общей форме — в виде трёх балок, соединённых друг с другом под прямыми углами. Под влиянием этой статьи в 1961 голландский художник Мауриц Эшер создал одну из своих знаменитых литографий «Водопад».[7]

13-метровая скульптура невозможного треугольника из алюминия была воздвигнута в 1999 году в городе Перт (Австралия)

1.5. Треугольник Паскаля

Самой известной математической работой Блеза Паскаля является трактат об «арифметическом треугольнике», образованном биномиальными коэффициентами (треугольник Паскаля), который имеет применение в теории вероятностей и обладает удивительными и занимательными свойствами.

В действительности, треугольник Паскаля был известен задолго до 1653 года — даты выхода «Трактата об арифметическом треугольнике». Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.

Мартин Гарднер пишет в книге «Математические новеллы» (М., Мир, 1974): «Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике».[9]

1.7. Треугольник Рёло

Треугольник Рёло – это область пересечения трех окружностей, построенных из вершин правильного треугольника. Они имеют радиус, равный стороне этого же треугольника. Он относится к разряду простых фигур (как круг), обладающих постоянной шириной. То есть если к нему провести две параллельные опорные прямые, то независимо от выбранного направления, расстояние между ними будет неизменным, в любой точке независимо от их длины.

По мнению историков, название это «непростой» простой фигуре дал немецкий механик Франц Рёло, живший с 1829 по 1905 годы. Многие историки сходятся в том, что именно он стал первооткрывателем свойств этой геометрической фигуры. Потому как он первый широко использовал свойства и возможности треугольника Рёло в своих механизмах.

Франц Рёло первым дал доскональные определения понятиям «кинетическая пара», «кинетическая цепь». Он впервые показал возможность связи между основами механики и конструирования. То есть связал теорию и практические проблемы конструирования. Что позволило создавать механизмы в совокупности их функциональных возможностей с внешней привлекательностью/эстетичностью. Отсюда Рёло стали считать поэтом механики. Что позволило последователям в корне пересмотреть имеющиеся в ней теории.

Иные исследователи первооткрывателем этой фигуры признают Леонарда Эйлер (18 век), который уже тогда продемонстрировал возможность его создания ее из трех окружностей.

А третьи «увидели» треугольник Рёло в рукописях гениального Леонардо Да Винчи. Манускрипты этого естествоиспытателя, с изображением этой «простой» фигуры, хранятся в Мадридском кодексе и в Институте Франции.

Но кто бы ни был первооткрывателем этот «не простой» треугольник получил широкое распространение в современном мире. А именно:

• Сверло Уаттса. В 1914 году Гарри Джеймс Уаттс изобрел уникальный инструмент для высверливания квадратных отверстий. Это сверло, выполнено в форме Треугольника Рёло;

• Двигатель Ванкеля. С 1957 года треугольник Рёло немецкий изобретатель Ванкель Ф. создал уникальный механизм. Где внутри камеры, цилиндрической формы, по сложной траектории передвигается ротор-поршень. Созданный в форме треугольника Рёло. При его постоянном движении, каждая его грань, контактируя со стенками камеры, образует сразу три камеры, названные позже «камерами сгорания».

• Грейферный механизм кинопроекторов. Треугольник Рёло, вписанный в квадрат и двойной параллелограмм лежат в его основе. А нужен он для равномерного продергивания кинопленки во время киносеанса со скоростью в 18 кадров/с без отклонений и задержек;

• в архитектуре. Конструкция из двух дуг треугольника Рёло образует стрельчатую арку готического стиля. А окна в форме Рёло стоят в Брюгге в церкви Богоматери. Как орнамент он присутствует и на оконных решетках швейцарской коммуны Отрив и цистерцианского аббатства.

Следовательно, изобретенный в прошлом веке треугольник Рёло широко используется сегодня. Однако его изучение не стоит на месте. Его свойства, как характеристики простой фигуры, находится в постоянном теоретическом и практическом изучении.[10]

1.8. Бермудский треугольник Бермудский треугольник – одно из самых мистических мест на нашей планете, изучить природу которого до сих пор не удалось человеку.

Это загадочное место находится в Атлантическом океане, между тремя географическими точками: Пуэрто-Рико, Флоридой и Бермудскими островами. Эти точки образуют геометрические «вершины» Бермудского треугольника.

Уже много лет, а точнее — с 1945 года, это «дьявольское морское место» считается очень опасным для мореплавателей. Здесь происходило множество необъяснимых явлений. Дрейфующие суда с мертвыми экипажами, бесследные исчезновения самолетов и морских судов, выход из строя навигационных приборов, датчиков, радиопередатчиков, часов – вот неполный список того, чем прославился на весь мир этот морской треугольник.

Многие ученые, астрономы, физики, математики, географы, и даже военные службы пытались разгадать мистику загадочных явлений, однако эти исследования не стали успешными. На сегодняшний день человеческий мир владеет только обыкновенными догадками, которые не дают однозначного ответа – что это за странное географическое место, что видят люди, попадая туда, куда пропадают исчезнувшие корабли и самолеты.

Вот такая вот странная загадка этого места с условными границами простой геометрической фигуры. Загадка, которую вряд ли когда-нибудь удастся решить.[12]

ПРАКТИЧЕСКАЯ ЧАСТЬ

Анкетирование – это метод эмпирического исследования, основанный на опросе значительного числа респондентов и используемый для получения информации о типичности тех или иных психолого-педагогических явлений. Этот метод дает возможность установить общие взгляды, мнения людей по тем или иным вопросам; выявить мотивацию их деятельности, систему отношений.[14]

Какие треугольники бывают?

Какими свойствами обладают треугольники?

Нужны ли треугольники в жизни людей?

Знаете ли вы почему Бермудский треугольник назван треугольником?

Видео:Математика Задача про треугольник с углами 20,80, 80 Бермудский треугольник в геометрииСкачать

Паранормальный фейк века. Что на самом деле скрывала загадка Бермудского треугольника

В январе 2020 года средства массовой информации, особенно научно-популярные, облетело сообщение о находке, сделанной в Атлантическом океане в 65 километрах к востоку от города Сент-Огастин на севере американского штата Флорида. Команда «охотников за кораблекрушениями» совместно со съемочной группой телеканала Science Channel обнаружила на глубине в 30 метров останки грузового парохода SS Cotopaxi, затонувшего почти столетие назад. Этот корабль, чье бесследное исчезновение стало уже легендарным, в свое время угодил даже в фильм Стивена Спилберга «Близкие контакты третьей степени», где послужил доказательством существования инопланетной цивилизации. С находкой «Котопахи» окончательно развенчан, наверное, главный миф второй половины XX века, десятилетиями будораживший неокрепшую психику миллионов обывателей. Таинственный Бермудский треугольник, необъяснимыми жертвами которого будто бы стали сотни кораблей, самолетов и тысячи людей, оказался очередным бизнес-проектом по сравнительно честному отъему денег у простодушного населения. Onliner рассказывает о загадке (и разгадке) этой «черной дыры» в океане.

Видео:Бермудский Треугольник - Загадка раскрыта!Скачать

Исчезновение «Котопахи»

29 ноября 1925 года грузовой пароход SS Cotopaxi, названный в честь почти 6-километрового эквадорского вулкана Котопахи, отправился в очередной, казалось бы, заурядный рейс. Из американского Чарльстона (штат Южная Каролина) он должен был доставить в столицу Кубы Гавану груз угля. Спустя два дня береговые службы получили с борта корабля сообщение о сильном крене судна, и с тех пор о нем никто ничего не слышал. Без вести пропало и оно само, и 32 человека, находившихся на борту. С этого момента и на протяжении почти века «Котопахи» являлся одним из главных героев выстроенного вокруг данного района Мирового океана мифа о неком Бермудском треугольнике, непостижимым науке образом пожирающем корабли, самолеты, а заодно и их экипажи.

Несчастный углевоз сделал героем своей культовой фантастики «Близкие контакты третьей степени» (1977) даже Стивен Спилберг. В этом фильме корабль спустя полвека после исчезновения находят в центральноазиатской пустыне Гоби — естественно, безо всякого следа команды на борту. Виноваты во всем оказались, как водится, инопланетяне.

В мае 2015 года появились сообщения о сенсационной находке. У побережья Кубы корабли береговой охраны страны перехватили дрейфующее судно, которое они идентифицировали как SS Cotopaxi. Конечно, это был «летучий голландец» без единого члена экипажа. Очень быстро выяснилось, что первоисточником этой «сенсации» являлся известный сатирический сайт фейковых новостей World News Daily Report, и о пароходе вновь забыли.

Окончательно загадка «Котопахи» была решена 4,5 года спустя. Команда исследователей во главе с Майклом Барнеттом, сотрудником Национального управления океанических и атмосферных исследований (NOAA) — американского государственного агентства, занимающегося изучением Мирового океана, — к январю 2020 года закончила тщательные исследования, в которых объединила теоретическую работу в архивах и практические погружения на морское дно. Документы британской страховой компании Lloyd’s, после пропажи корабля судившейся с родственниками членов его команды, позволили установить, что последние радиосообщения с борта SS Cotopaxi были получены в районе флоридских городов Джексонвилль и Сент-Огастин. Известный маршрут парохода и точка его последнего выхода на связь позволили соотнести исчезновение с уже известным дайверам местом крушения неопознанного судна в 65 километрах к западу от побережья штата.

Благодаря серии погружений это предположение проверили на практике. Оказалось, что габариты затонувшего безымянного корабля и доступные на дне фрагменты совпадают с внешним обликом «Котопахи». Кроме того, среди поднятых на поверхность деталей судна обнаружились и элементы, произведенные в непосредственной близости от верфи, где был построен углевоз.

Пароход построили в 1918 году, еще в Первую мировую войну, для нужд американской военной промышленности. За семь лет корабль успел угодить в два серьезных инцидента: в июне 1919-го он сел на мель в Бразилии и был снят с нее с серьезными повреждениями, в том числе двигателей, а в 1920-м в гаванском порту судно столкнулось с местным буксиром. Несмотря на относительную молодость, в свое последнее плавание SS Cotopaxi ушел изрядно потрепанным. К тому же, как показала история кораблей его серии, скорее всего, у парохода были определенные конструктивные недостатки — слишком много «систершипов» из этого семейства в итоге затонуло при разных обстоятельствах. Судя по всему, на стыке осени и зимы 1925 года «Котопахи» угодил в шторм, и корпус судна не перенес ненастье. Инопланетяне вновь оказались ни при чем. Более того, легендарная жертва Бермудского треугольника вообще затонула за его пределами. История старого корабля в очередной раз показала, что все выстроенные вокруг этого «проклятого» места мифы на самом деле череда преимущественно древних фактов, обернутых в оболочку выдумок, недоговорок и откровенных фантазий.

Видео:БЕРМУДСКИЙ ТРЕУГОЛЬНИК 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Рождение мифа

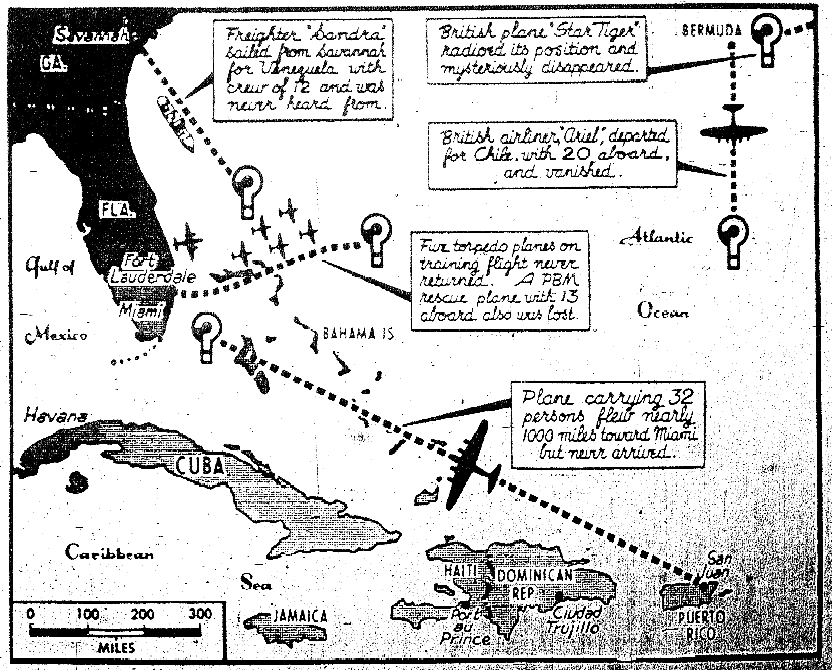
На самом деле Бермудский треугольник — довольно позднее изобретение. На «аномальную» концентрацию кораблекрушений и исчезновений самолетов обратили внимание только после окончания Второй мировой. 17 сентября 1950 года в газете Miami Herald вышла заметка «Загадки моря до сих пор сбивают с толку людей в современном мире». В ней журналист Эдвард ван Винкл Джонс перечислил несколько катастроф последних лет, причины которых так и не были установлены. Пять военных самолетов вылетели в тренировочный полет с флоридской военно-воздушной базы и исчезли. Пассажирский лайнер, направлявшийся из Пуэрто-Рико в Майами, так и не добрался до места назначения. Еще один гражданский самолет, летевший из Лондона в Чили и сделавший промежуточную посадку на Бермудских островах, пропал вскоре после вылета из тропического рая. Сухогруз с 300 тоннами удобрений вышел из порта Саванны (штат Джорджия) в Венесуэлу, и больше о нем не слышали.

Автор материала не делал никаких паранормальных предположений. Его месседж заключался в том, что даже в нашем современном мире увеличивающихся скоростей, реактивных полетов, радиосвязи человек остается бессилен перед морской стихией. Заметка при этом сопровождалась картой, на которой впервые были намечены канонические границы того самого треугольника.

«Проведите линию от Флориды к Бермудским островам, оттуда — к Пуэрто-Рико и обратно к Флориде через Багамы. В этом-то треугольнике и происходит большинство кораблекрушений».

Спустя 14 лет этот термин был наконец сформулирован. В 1964 году в статье «Смертоносный Бермудский треугольник», опубликованной в бульварном журнале Argosy, а затем в вышедшей годом спустя книге «Невидимые горизонты» Винсент Гэддис определил границы территории, где, по его мнению, концентрация необъяснимых исчезновений превышала допустимую. Условные вершины треугольника находились на Бермудских островах, в районе Майами и на острове Пуэрто-Рико.

Своими материалами Гэддис, вероятно сам того не предполагая, открыл дорогу бесконечному числу последователей, принявшихся спекулировать на теме происходящего в этом участке Мирового океана. В 1960—80-е годы были написаны тысячи газетных и журнальных статей, сотни книг, выпущены документальные и художественные книги, где в той или иной степени муссировались реальные и выдуманные катастрофы. «Библией» сторонников паранормальной версии стала книга Чарльза Берлица «Бермудский треугольник», опубликованная в 1974 году. В ней автор приводит почти полторы сотни «таинственных феноменов», связанных с исчезновением кораблей и самолетов. Номенклатура приводимых объяснений происходящему невообразимо велика: за гибель или пропажу людей ответственны жители Атлантиды и инопланетяне, на крайний случай — огромные магнитные воронки или какие-нибудь морские чудовища. Любопытно, что тема Бермудского треугольника была популярна и в, казалось бы, насквозь материалистическом Советском Союзе. Оказалось, что фантазии на тему сверхъестественного не чужды кодексу строителя коммунизма.

В этой своей книге и в последовавших за ней многочисленных продолжениях Берлиц и его соратники приводили в том числе и достоверные факты. Действительно, 5 декабря 1945 года с базы ВМС США в Форт-Лодердейле для выполнения тренировочных бомбометаний в сторону Багамских островов вылетело звено из пяти бомбардировщиков-торпедоносцев типа «Эвенджер». Назад эти самолеты так и не вернулись, никаких следов найдено не было. При поисках исчезнувших пропал еще один гидросамолет — «Мартин Маринер».

28 декабря 1948 года вылетевший из города Сан-Хуан (остров Пуэрто-Рико) пассажирский Douglas DC-3DST «Dakota» с 32 людьми на борту так и не добрался до места назначения. Место катастрофы найдено не было, точная причина крушения не установлена. Точно так же не ясно и то, что случилось с военно-транспортным Lockheed R7V-1 Super Constellation ВМС США, исчезнувшим в ночь с 30 на 31 октября 1954 года.

Никто не оспаривает и потерю сухогруза USS Cyclops, пропавшего в районе Бермудского треугольника 4 марта 1918 года вместе с грузом марганцевой руды и экипажем в 306 человек, — крупнейшая потеря в истории американского флота, не связанная с боевыми действиями, хоть и случившаяся в годы Первой мировой. Точно таким же фактом остается и исчезновение в феврале 1963 года у южного побережья Флориды танкера SS Marine Sulphur Queen с командой из 39 моряков.

Все эти трагедии документально зафиксированы, и за каждой из них стоят десятки, иногда сотни человеческих жизней. Подобные инциденты можно перечислять очень долго. Сторонники аномальных теорий утверждают, что за гибель такого количества людей ответственно что угодно, кроме естественных сил природы. На самом деле этими «исследователями» движут обыкновенные спекуляции на человеческих страхах и любопытстве, вызванные желанием продать побольше экземпляров своих текстов. Пусть иногда картина катастроф, случившихся в Бермудском треугольнике, не до конца ясна, но абсолютно все из них можно объяснить без использования фантазий об инопланетных вторжениях.

Видео:Бермудский Треугольник Реальность или Фантастика? Документальный фильм National Geographic 2021Скачать

Аллея ураганов

Первым серьезными разоблачениями бермудских мистификаторов занялся писатель Ларри Куше. Уже в 1975-м, через год после издания «Бермудского треугольника» Чарльза Берлица, он выпустил свой ответ на эту работу — «Загадка Бермудского треугольника: разгадана» (в 1978-м книга вышла в СССР под названием «Бермудский треугольник: мифы и реальность»). В ней Куше провел анализ всех приведенных оппонентом «аномалий», после чего выяснилось, что Берлиц неоднократно использовал подлоги, фантазии, домыслы, ничем не обоснованные предположения и, наконец, обычное вранье. Оказалось, что некоторые из описанных «исследователем бермудского феномена» инцидентов произошли за пределами треугольника (в одном случае даже в Тихом океане, за тысячи километров). В других ничего таинственного не было, так как причины катастроф были расследованы и обнародованы. Некоторые «исчезновения» происходили во время жестоких тропических ураганов, о которых Берлиц «забывал» упомянуть, утверждая, что «погода была отличной». Были даже катастрофы, про которые Куше не смог найти никаких упоминаний в прессе, то есть выдуманные от начала и до конца.

Главный вывод автора — Берлиц и ему подобные либо шарлатаны, не умеющие работать с документальными источниками, либо мошенники, сознательно вводящие в заблуждение своих читателей ради погони за сенсацией.

Никакого аномально высокого количества происшествий в Бермудском треугольнике не случается. Если их число и превышает средние показатели, то исключительно из-за того, что данный район в принципе является сверхоживленным перекрестком многочисленных морских и воздушных путей как внутри региона, так и между континентами: Америками, Африкой и Европой. Вдобавок именно здесь наблюдается сложная система течений, из-за которых, по утверждению специалистов, не всегда можно обнаружить точное место того или иного инцидента. Кроме того, катастрофам способствует как сложный рельеф дна, так и наличие большого количества отмелей, что осложняет навигацию и в условиях неустойчивой погоды оказывает прямое влияние на безопасность кораблей.

Фактор погоды имеет первостепенное значение. В северной части Атлантического океана, между Африкой и Северной Америкой, находится зона, получившая название Аллея ураганов. Именно здесь летом и осенью формируются многочисленные тропические депрессии, пика своей интенсивности (и статуса урагана) достигающие как раз в районе Мексиканского залива и Бермудского треугольника. Ураганы с мощными штормами стремительны, непредсказуемы и безжалостны. Практически каждый год в сводках СМИ фигурирует очередная условная Катрина, наносящая региону ущерб на десятки, а порой даже сотни миллиардов долларов. Стоит ли удивляться, что порой жертвами ненастья становятся корабли и самолеты.

«Звено 19», пять бомбардировщиков, отправившихся в тренировочный полет в декабре 1945 года и бесследно пропавших, судя по восстановленной картине развития событий, просто заблудились, в эпоху отсутствия GPS сделав неправильные расчеты и перепутав визуальные опорные точки. Приписываемые им «охотниками за сенсациями» слова про необычно выглядящий океан («Мы опускаемся в белые воды…») — просто очередная выдумка. После того как у самолетов закончилось топливо, они, скорее всего, были вынуждены приводниться и затонули целиком, что объясняет отсутствие на поверхности океана следов крушения.

У вылетевшего в 1948-м из города Сан-Хуан (остров Пуэрто-Рико) пассажирского Douglas DC-3DST «Dakota» был ряд технических проблем (с двигателем и радиостанцией), оказавшихся критическими в условиях ограниченного запаса топлива и ночного рейса. Экипаж просто не получил сообщение об изменившемся направлении ветра, который снес самолет с верного курса на Майами в Мексиканский залив.

В конструкции пропавшего в 1918-м с грузом марганца парохода USS Cyclops впоследствии были выявлены серьезные недостатки, которые при определенных условиях (нарушение центровки груза и сильная нагрузка) могли привести к разрушению корпуса. Судя по архивным данным, в дни исчезновения корабля в этом районе наблюдался тропический шторм. К тому же два из оставшихся трех «систершипов», построенных по тому же проекту, были потеряны при похожих обстоятельствах в годы Второй мировой.

Перевозивший в 1963-м расплавленную серу танкер SS Marine Sulphur Queen также угодил в шторм, а последующее расследование показало, что судно было просто непригодно к эксплуатации и давно должно было быть отправлено на лом.

Бóльшая часть инцидентов, произошедших в Бермудском треугольнике, случилась давным давно, в эпоху, когда эффективных метеорологических и спасательных служб просто не существовало, как не было и систем геопозиционирования и спутникового контроля. Люди в принципе слабо понимали Мировой океан как комплексную систему, не умели предсказывать его поведение, выбирать безопасные схемы работы с ним и в его условиях. Да и техника была в принципе менее надежной, более уязвимой перед внешними факторами. В бесследных исчезновениях, особенно самолетов, в ту эпоху нет ничего удивительного. Такое случается и сейчас, достаточно вспомнить историю рейса 370 Malaysia Airlines в 2014 году.

Пик увлечения темой Бермудского треугольника пришелся на 1960—70-е и по мере развития науки и техники сходил на нет. Внезапно даже самые внушаемые люди поняли, что почему-то новые происшествия в этой «аномальной зоне» практически не случаются, а авторы очередных «сенсационных» опусов по-прежнему жонглируют преданиями многолетней давности.

1 октября 2015 года в Бермудском треугольнике исчез американский контейнеровоз SS El Faro с 33 моряками на борту, шедший из Джексонвилла (Флорида) в Сан-Хуан (Пуэрто-Рико). Очередная жертва инопланетян? Нет, человеческая ошибка: капитан судна завел его прямиком в мощный ураган Хоакин. То, что раньше считалось бы несомненным доказательством существования необъяснимого, при современном уровне расследования катастроф оказалось обычной халатностью. Останки контейнеровоза были обнаружены на дне, тела членов экипажа так и не нашли.

Разгадка тайны парохода SS Cotopaxi, похоже, поставила окончательную точку в бизнес-проекте под названием «Бермудский треугольник». Конечно, некоторая аудитория у этой теории заговора будет всегда, как будут появляться и будоражащие воображение тексты и фильмы, но очень уставшая тема уже вряд ли позволит зарабатывать на ней миллионы, оставшись уделом крайне ограниченной секты.

Суши и роллы, чтобы негрустно и вкусно проводить апрель в изоляции. Есть в наличии

Видео:Самые известные тайны Бермудского треугольника: правда или вымысел?Скачать

Урок математики «Тайна бермудского треугольника

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ конспект урока.doc

Видео:Краткая история Бермудского треугольникаСкачать

Урок математики в 5 клас c

Видео:Бермудский треугольник | Почему? Вопросы мироздания | DiscoveryСкачать

Тема урока: Треугольник. Виды треугольников.

Видео:Выживший летчик рассказал, что он увидел в Бермудском треугольникеСкачать

Вид урока: урок изучения и первичного закрепления новых знаний.(технология перевернутый класс)

Видео:КАК БЕРМУДСКИЙ ТРЕУГОЛЬНИК ВСЕХ ОБМАНЫВАЛ???Скачать

Класс: 5

— предметные: научить учащихся классифицировать треугольник по видам их углов и по количеству равных сторон.

— личностные : вызвать интерес к изучению темы и желание применить приобретенные знания и умения, формировать умение работать в парах, группах и находить согласованные решения.

— метапредметные: формировать умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать.

• ПК, проекционное оборудование, интерактивная доска
• Заготовки треугольников, раздаточный материал

Формы работы учащихся: индивидуальная, групповая технология, ИКТ.

Видео:На Аляске есть Бермудский треугольник, и он еще более загадоченСкачать

Этапы урока

Видео:100 Фактов о Бермудском Треугольнике, о Которых Вы не ЗналиСкачать

Задачи этапа

Видео:Факты и мифы о Бермудском треугольнике: викторинаСкачать

Визуальный ряд

Видео:5 Самых Страшных Тайн Бермудского ТреугольникаСкачать

Деятельность учителя

Видео:Почему Бермудский треугольник не найти на картеСкачать

Деятельность учащихся

Видео:Бермудский монстр | Проклятие Бермудского треугольника | DiscoveryСкачать

Формируемые УУД

Видео:НЛО и Бермудский треугольник. Леденящий ужас.Скачать

Организационный момент

Видео:ВСЕ ТАЙНЫ БЕРМУДСКОГО ТРЕУГОЛЬНИКА [Топ Сикрет]Скачать

Определить тему и цель урока

Видео:Необъяснимые встречи | Проклятие Бермудского треугольника | DiscoveryСкачать

видеоролик

Видео:Бермудский треугольник раскрыт: Разгадка величайшей морской тайны!Скачать

интерактивная доска

Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.

Ребята скажите, любите ли вы путешествовать. Каждый из вас хотел бы оказаться в чудесном месте где светит солнце, тепло, море. В мире есть много необычных и загадочных мест где кроится много тайн природы. С одним из таких мест мы сегодня познакомимся

О каком месте идет речь?

Какая связь фильма и темы урока?

В правильности формулировки темы нам поможет АНАГРАММА

Ребята у вас есть что то общее?

А есть то что отличает вас друг от друга?

Так и треугольники все разные и мы рассмотрим их виды

Включаются в деловой ритм урока

Запись темы урока1

Ответы учеников:

-Ученики

Ответы учеников:

-Национальность

-Цвет волос и т.д

Запись темы урока2

Регулятивные – умение организовывать себя, настраиваться на работу.

Развитие внимания, эстетического вкуса.

Обеспечение мотивации учения детьми, принятия ими целей урока

Сегодня мы узнаем, что такое треугольник, научимся классифицировать треугольники.

Регулятивные: видение, постановка, принятие познавательной цели.

Актуализация знаний и умений

Актуализация опорных знаний и способов действий

Работа в рабочей карте МАТЕМАТИЧЕСКИЙ ДИКТАНТ

Если высказывание правильное ставим 1 если неправильное ставим 0

1. Угол меньше 90 градусов острый (1)

2. Отрезок соединяющий центр окружности с любой его точкой это радиус(1)

3. Развернутый угол равен двум прямым углам(1)

4. Самая большая хорда -это радиус(0)

5. Угол равный 90 градусов прямой(1)

6. Углы измеряются в градусах, сантиметрах и минутах(0)

7. Инструмент для измерения углов- транспортир(1)

8. Диаметр равен двум радиусам(1)

9. Угол больше 90 градусов но меньше 180 это тупой угол (1)

10.Если у фигуры три угла то это треугольник (1)

Один у доски, остальные работают на рабочих листах

Развитие самостоятельности, самоконтроля, стрессоустойчивости.

Коммуникативные: умение оформлять свои мысли в письменной форме

Усвоение новых знаний и способов усвоения

Обеспечение восприятия, осмысления и первичного запоминания детьми изучаемой темы: треугольник

Работа в рабочей карте

Отметьте в тетради три точки так, чтобы они не лежали на одной прямой, и соедините попарно эти точки. Кая фигура у вас получилась? Самым простым многоугольником является треугольник.

1 Измерить стороны

2. Определить вид треугольника

3. Найти периметр

4. Измерить углы

1 Измерить углы

2. Определить вид треугольника

3. Измерить стороны

4. Найти периметр

Выполняют практическое задание в тетради

Работа в группах( определение вида треугольников защита работы(характеристика)

Познавательные: работа с определением и понятиями

Развитие эрудиции, познавательного интереса.

Ориентирование на изученный материал

Понимание представляемой информации,

Анализ речевых конструкций

Физминутка для рук и расслабления глаз

А братишка мой, Сережа, Математик и чертежник — На столе у бабы Шуры Чертит всякие. (фигуры)
Три угла, три стороны, — Ну, пожалуй, и довольно! — Что ты видишь? — . (Треугольник)
Эта странная фигура, Ну, совсем миниатюра! И на маленький листочек Мы поставим сотни . (точек)
Он от солнца прилетает, Пробивая толщу туч И в тетрадочке бывает, А зовется просто — . (луч)
Едет ручка вдоль листа По линеечке, по краю — Получается черта, Называется . (прямая)
Он и острый, да не нос, И прямой, да не вопрос, И тупой он, да не ножик, — Что еще таким быть может? (угол)
Ноги очень интересны У таинственного друга: Если первая на месте, То другая ходит кругом! (циркуль)

Ученики выполняют упражнения

Познавательные: умение использовать полученные знания

Организация первичного закрепления

Установление правильности и осознанности изучения темы «Треугольники. Виды треугольников».

Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу.

Разбить треугольники по группам

Определить вид треугольника по обозначениям на чертеже

Кроме у треугольника есть другие пространственные родственники

А почему эти геометрические тела являются родственниками треугольника?

Ребята устно определяют, к какому виду относится каждый треугольник, подробно поясняя свой ответ.

Ученики рассматривают модели

Делают вывод. Выводы заслушиваются

Оформление своих мыслей в устной форме, умение взаимодействовать с соседом при выполнении учебной задачи

Обмен знаниями для принятия эффективных совместных решений

Дополнительная информация

Треугольники в жизни людей

1. В разных направлениях

3. В архитектуре

Подведение итогов урока, рефлексия

Дать качественную оценку работы класса и отдельных учащихся

Вы замечательно поработали на уроке. Надеюсь, этот материал вы не забудете. Думаю, что знания, которое вы получили сегодня, помогут вам на уроках геометрии в старших классах.

Регулятивные: Структурирование знаний.

Информация о домашнем задании

Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания

Ваше домашнее задание:

Найти в каких областях еще мы можем встретить треугольник

Рефлексия

Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации, их собственной деятельности и взаимодействия с учителем и другими детьми в классе

· Мне не понравилось …

Спасибо за урок.

Регулятивные: Оценка качества и уровня знаний.

Выбранный для просмотра документ рабочая карта.docx

Рабочая карта урока

1. Математический диктант

2. Практическая работа

Характеристик(стороны и углы)

4. Треугольники в жизни_____________________________________________

Выбранный для просмотра документ раздатка.docx

1

Практическая работа 1

1 Измерить стороны

2. Определить вид треугольника

3. Найти периметр

4. Измерить углы

2

Практическая работа 1

1 Измерить стороны

2. Определить вид треугольника

3. Найти периметр

4. Измерить углы

Практическая работа 1

1 Измерить стороны

2. Определить вид треугольника

3. Найти периметр

4. Измерить углы

Практическая работа

1 Измерить углы

2. Определить вид треугольника

3. Измерить стороны

4. Найти периметр

Практическая работа

1 Измерить углы

2. Определить вид треугольника

3. Измерить стороны

4. Найти периметр

Практическая работа

1 Измерить углы

2. Определить вид треугольника

3. Измерить стороны

4. Найти периметр

З нать желает каждый школьник
Что такое треугольник.

Треугольник — это клин,
Треугольником трамплин
Высится над миром,

Клином в небе журавли
Пролетают мимо

Праздничная елка —
Тоже «треуголка».

Парус в море, всех ветров
На земле поборник,
С виду — треугольник.

И беляш, и пирамида —
Треугольнейшего вида.

Иногда журнальный столик
Так похож на треугольник.

Трегольно — помело,
Треугольное — весло.

Уплетая не в гостях
Аппетитнейший рассольник,
Папа, мама и дитя —
Есть семейный треугольник.

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 958 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 554 845 материалов в базе

Материал подходит для УМК

«Математика», Никольский С.М., Потапов М.К., Решетников Н.Н. и др.

Другие материалы

• 01.10.2021
• 140
• 6

• 01.10.2021
• 111
• 2

• 01.10.2021
• 102
• 1

• 01.10.2021
• 100
• 0

• 01.10.2021
• 203
• 6

• 01.10.2021
• 528
• 95

• 01.10.2021
• 464
• 11

• 01.10.2021
• 215
• 5

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 01.10.2021 246
• RAR 21.4 мбайт
• 7 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Северина Татьяна Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 8 лет и 2 месяца
• Подписчики: 0
• Всего просмотров: 4927
• Всего материалов: 8

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Египте нашли древние школьные «тетрадки»

Время чтения: 1 минута

Общество «Знание» в 2022 году планирует запустить серию хакатонов и школу лекторов

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

В «Единой России» предложили ввести раздел безопасности детей в интернете в курс ОБЖ

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.