Атанасян медиана прямоугольного треугольника (2 видео)

Свойства медианы в прямоугольном треугольнике с доказательствами

В этой статье мы рассмотрим свойства медианы в прямоугольном треугольнике, а также их доказательства.

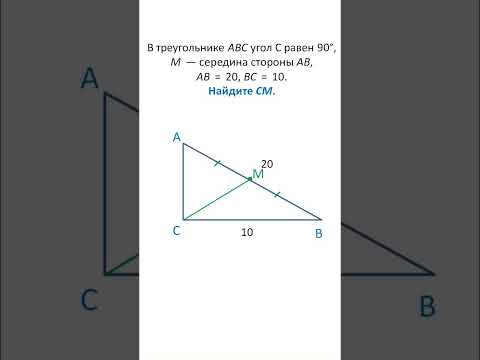
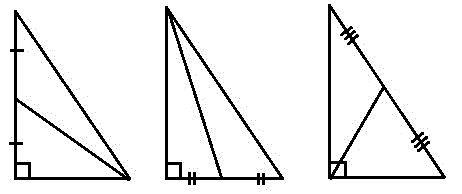
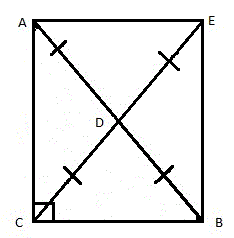
Медиана — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Для прямоугольного треугольника это будут медианы, проведённые с острого угла к серединам катетов или с прямого к центру гипотенузы (рис. 1).

Содержание

Свойства медианы в прямоугольном треугольнике
Доказательства свойств
Первое свойство
Доказательство:
Второе свойство
Доказательство:
Третье свойство
Доказательство:
Технологическая карта урока геометрии по теме «Свойство медианы прямоугольного треугольника» (7 класс)
Определение и свойства медианы прямоугольного треугольника
Определение медианы прямоугольного треугольника
Свойство 1
Свойство 2
Свойство 3
Пример задачи
🔍 Видео

Видео:Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать

Свойства медианы в прямоугольном треугольнике

Медианы в прямоугольном треугольнике пересекаются в одной точке, а точка пересечения делит их в соотношении два к одному считая от вершины, из которой проведена медиана.
Медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы.
Медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Видео:№404. Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузеСкачать

Доказательства свойств

Первое свойство

Доказать, что медианы в прямоугольном треугольнике пересекаются в одной точке и делятся в пропорции 2:1, считая от вершины.

Доказательство:

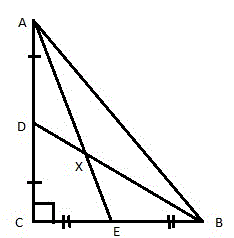
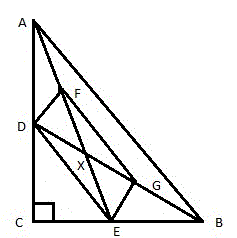
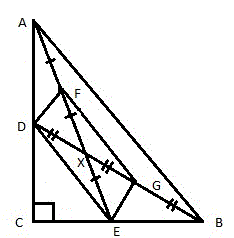
Рассмотрим прямоугольный треугольник ABC. Проведем две медианы AE и BD, которые пересекаются в точке X (рис. 2).

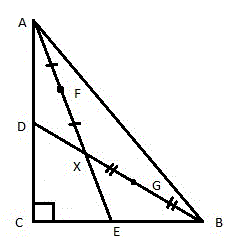
Середины отрезков AX и BX обозначим, соответственно, буквами F и G (рисунок 3).

Соединим между собой точки (D, F, G и E) и получим четырёхугольник DFGE (рис. 4).

Сторона DE этого четырёхугольника будет средней линией треугольника ABC. Согласно определению: отрезок, соединяющий середины двух сторон треугольника, является его средней линией. При этом по свойству средняя линия параллельна не пересекающейся с ней стороне и равна половине этой стороны, то есть.
DE || AB и DE = AB / 2.

Аналогично сторона FG треугольника AXB будет его средней линией.
FG || AB и FG = AB / 2

Отсюда следует, что отрезки DE и FG являются параллельными и равными. Следовательно, четырехугольник DFGE – параллелограмм (по признаку параллелограмма).

Так как диагонали параллелограмма в точке пересечения делятся пополам, то
FX=XE, GX=XD

Так как AF = FX (по построению), то и AF = FX = XE, аналогично DX = XG = GB.

Получается, что точка X делит обе медианы AE и BD в соотношении 2 к 1 считая от вершины треугольника.

Аналогично, мы сможем доказать, что точка пересечения 3-ей медианы, проведенной из прямого угла к гипотенузе, с медианой AE (или BD) будет делить ее в соотношении 2 к 1, считая от вершины. То есть наша 3-я медиана также пройдет через точку X. Отсюда следует, что все 3 наши медианы пересекаются в одной точке.

Что и требовалось доказать.

Второе свойство

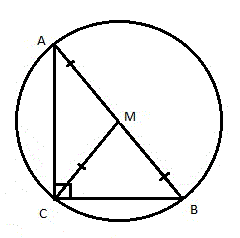
Доказать, что медиана, проведённая с вершины прямого угла к гипотенузе, равна половине гипотенузы.

Доказательство:

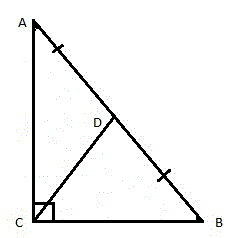
Чтобы доказать это свойство рассмотрим прямоугольный треугольник ABC и проведём медиану к гипотенузе. Точку ее пересечения с гипотенузой обозначим буквой D (рис. 6).

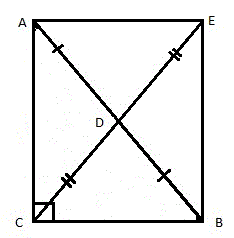
Отразим симметрично наш треугольник ABC относительно отрезка AB (рисунок 7). В результате получим четырёхугольник AEBC, в котором AD=DB (поскольку CD медиана к стороне AB) и CD=DE (по построению). То есть диагонали четырехугольника AEBC пересекаются и точкой пересечения делятся пополам. Отсюда следует, что AEBC является параллелограммом (по признаку параллелограмма).

Один из признаков прямоугольника говорит о том, что параллелограмм является прямоугольником, если хотя бы один из его углов прямой. Поскольку ∠ACB прямой (по построению), то AEBC — прямоугольник.

Поскольку диагонали прямоугольника равны и в точке пересечения делятся пополам (свойство прямоугольника), то AB = CE и AD = DB = CD = DE.

Так как AB = AD + DB, AD = BD и СD = AD = BD, то получается, что медиана AD, проведенная к гипотенузе AB равна половине ее длины.

Что и требовалось доказать.

Третье свойство

Доказать, что медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Доказательство:

Опишем вокруг прямоугольного треугольника ABC окружность.

Поскольку точка C уже лежит на окружности, то для того, чтобы доказать, что медиана CM является радиусом, нам надо доказать, что точка M – центр описанной окружности (т.е. равноудалена от нее).

Так как медиана делит отрезок пополам, а медиана проведенная к гипотенузе равна ее половине (согласно доказанному выше свойству), то точка M будет равноудалена от всех вершин треугольника, которые в свою очередь касаются окружности (рисунок 8).

Отсюда следует, что окружность, описанная вокруг прямоугольного треугольника ABC будет иметь центр на середине гипотенузы (в точке M), а медиана CM будет радиусом описанной окружности.

Что и требовалось доказать.

Понравилась статья, расскажите о ней друзьям:

Видео:ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

Технологическая карта урока геометрии по теме «Свойство медианы прямоугольного треугольника» (7 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Технологическая карта урока геометрии в 7 классе по теме

« Свойство медианы прямоугольного треугольника »

Морозова Татьяна Владимировна , учитель математики

Цели урока: создание ситуации на уроке, в которой обучающиеся «откроют» новые знания; организация продуктивной деятельности школьников, направленной на достижение ими результатов:

обучающие: помочь учащимся «открыть» свойство медианы прямоугольного треугольника, формировать умение применять данное свойство при решении задач базового уровня.

развивающие: развивать умения

предметные: умение формулировать свойства прямоугольного треугольника, понимать суть доказательства свойств.

метапредметные: умение использовать для познания окружающего мира различные методы (наблюдение, опыт, моделирование и др.); исследовать несложные практические ситуации с прямоугольным треугольником, выдвижение предположений о свойствах прямоугольного треугольника; развивать математическую речь, умение вступать в речевое общение, участвовать в диалоге; формирование умений воспринимать, перерабатывать и предъявлять информацию в словесной, образной, символической формах.

личностные: самостоятельность в приобретении новых знаний и практических умений; повышение интереса к предмету, уровень мотивации через задачи с практическим содержанием, исследовательскую деятельность.

воспитывающие: формирование представления о методах научного познания: наблюдение, исследования, эксперимента, выдвижения гипотез.

Тип урока: урок построения нового знания, творческая исследовательская деятельность.

Формы урока: фронтальная; проблемно-поисковая; эксперимент.

Оборудование: ПК, проектор и экран.

Преподавание ведется по учебнику Геометрия 7-9 классов общеобразовательных учреждений / под редакцией Л.С. Атанасяна и др. М.: Просвещение, 2013 год.

Повторение изученного материала.

Проверка домашнего задания

— Над какой темой мы работали на предыдущих уроках геометрии?

— Откройте тетради с домашней работой, проверяем задачу №1.

№ 1. В прямоугольном треугольнике АВС с прямым углом А проведена высота АD. Найдите ВС, если угол С равен 45°, АD = 8дм.

— Какое свойство прямоугольного треугольника вы использовали при решении этой задачи? Сформулируйте его.

— Какие еще свойства прямоугольного треугольника вы знаете. Сформулируйте их.

— Свойства прямоугольного треугольника.

На доске решение одного из учеников, он объясняет свое решение и отвечает на поставленные вопросы.

Формулируют свойства прямоугольного треугольника

Учится структурировать информацию в нужной форме

Учится составлять план действий; понимает, что уже освоено и чему предстоит научиться.

Осознает смысл учения и понимает личную ответственность за будущий результат;

учится сотрудничать с другими людьми.

Целеполагание и мотивация

— Как вы думаете, это все свойства, которые выполняются для прямоугольного треугольника?

— Да, действительно, мы еще не все знаем про прямоугольный треугольник.

При изучении геометрии мы постепенно будем расширять знания, рассматривать новые теоремы, связанные с этим треугольником.

— Как вы думаете, теоремы придумывают или открывают?

— Как происходят такие открытия?

— Может быть, и мы попробуем что-либо открыть? Ну, если не новое для всех, то новое для вас.

— Сформулируйте цель нашего сегодняшнего урока.

Отвечают на вопросы

— Люди наблюдают, анализируют, сравнивают.

Учащиеся определяют цель урока

— Открыть новые теоремы.

Учится слушать и слышать; выражать свои мысли, строить высказывание в соответствие с задачами коммуникации.

Учится ставить учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что ещё неизвестно.

Организация совместного обсуждения, установления сотрудничества с учителем, речевая коммуникация. Проявление интереса к новому содержанию.

Проверяем задачу №2 из домашней работы.

№ 2. В треугольнике АВС проведена медиана АМ. Определите вид треугольника АВС, если ВС = 15 см, АМ = 7,5 см.

— Рассмотрим следующую задачу (чертеж и условие задачи на слайде): В треугольнике МКР проведена медиана МЕ. Определите вид треугольника МКР, если МЕ = 10 дм, КР = 20 дм.

— Изменится ли решение? Зависит ли решение задачи от длин медианы и стороны, к которой проведена медиана?

— Как связаны длина медианы и длина стороны, к которой она проведена?

— Можем ли мы в этом случае определить вид треугольника?

— Сделайте вывод. Сформулируйте утверждение, используя связку «Если …, то…»

— Запишите число, классная работа. Оставьте свободную строчку для темы урока.

Запишите данную теорему в тетрадь и выделите.

— Доказательство данного утверждения будет отличаться от решения задач, которые мы рассмотрели?

Это будет ваше домашнее задание.

На доске решение одного из учеников, он объясняет свое решение и отвечает на поставленные вопросы.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Определение и свойства медианы прямоугольного треугольника

В данной статье мы рассмотрим определение и свойства медианы прямоугольного треугольника, проведенной к гипотенузе. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Определение медианы прямоугольного треугольника

Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми ( Свойства медианы прямоугольного треугольника

Свойство 1

Медиана (AD) в прямоугольном треугольнике, проведенная из вершины прямого угла (∠BAC) к гипотенузе (BC), равна половине гипотенузы.

BC = 2AD
AD = BD = DC

Следствие: Если медиана равняется половине стороны, к которой она проведена, то данная сторона является гипотенузой, а треугольник – прямоугольным.

Свойство 2

Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.

Для нашего треугольника (см. рисунок выше):

Это следует из теоремы Пифагора и Свойства 1.

Свойство 3

Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу описанной вокруг треугольника окружности.

Т.е. BO – это одновременно и медиана, и радиус.

Примечание: К прямоугольному треугольнику также применимы общие свойства медианы, независимо от вида треугольника.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Пример задачи

Длина медианы, проведенной в гипотенузе прямоугольного треугольника, составляет 10 см. А один из катетов равен 12 см. Найдите периметр треугольника.

Решение
Гипотенуза треугольника, как следует из Свойства 1, в два раза больше медианы. Т.е. она равняется: 10 см ⋅ 2 = 20 см.

Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b 2 = с 2 – a 2 = 20 2 – 12 2 = 256.
Следовательно, b = 16 см.

Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:
P_△ = 12 см + 16 см + 20 см = 48 см.