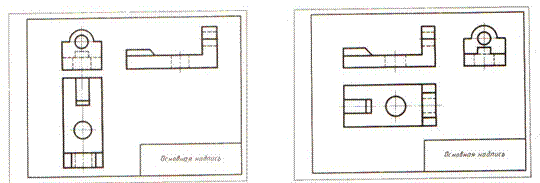
В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.
Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.
Ниже будут рассмотрены основные типы сопряжений.
- Сопряжение углов (Сопряжение пересекающихся прямых)
- Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
- Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
- Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
- Сопряжение параллельных прямых линий
- Сопряжение окружностей(дуг) с прямой линией
- Внешнее сопряжение дуги и прямой линии
- Внутреннее сопряжение прямой линии с дугой
- Сопряжение окружностей (дуг)
- Внешнее сопряжение дуг окружностей
- Внутреннее сопряжение дуг окружностей
- Смешанное сопряжение дуг окружностей
- Сопряжения в инженерной графике на чертежах с примерами
- Сопряжение двух пересекающихся прямых линий
- Сопряжения прямой с окружностью
- Сопряжение двух окружностей
- Построение касательных
- Принципы построение сопряжений
- 📹 Видео
Видео:СОПРЯЖЕНИЕ ОКРУЖНОСТИ С ЛИНИЕЙ [pairing the circle with the line]Скачать
![СОПРЯЖЕНИЕ ОКРУЖНОСТИ С ЛИНИЕЙ [pairing the circle with the line]](https://i.ytimg.com/vi/oKj3m1n67wI/0.jpg)
Сопряжение углов (Сопряжение пересекающихся прямых)
Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
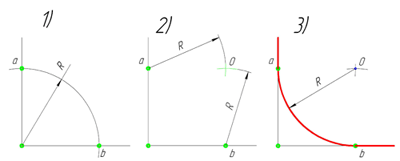
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
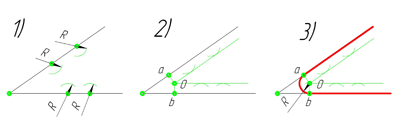
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
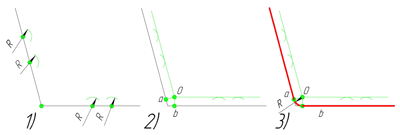
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.
Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение параллельных прямых линий
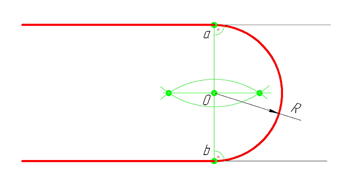
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.
Видео:1 2 4 сопряжение окружностейСкачать

Сопряжение окружностей(дуг) с прямой линией
Внешнее сопряжение дуги и прямой линии
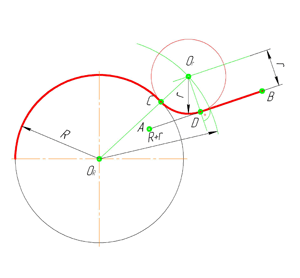
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.
Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности O R радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой О r .
Из центра сопряжения, точки О r , опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности О R и центр сопряжения О r линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.
Внутреннее сопряжение прямой линии с дугой
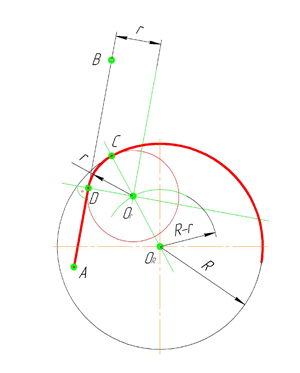
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности O R радиусом R-r. Точка О r , полученная на пересечении прямой и дуги, и будет центром сопряжения.
Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.
Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности О R прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки О r , центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.
Видео:Внешнее сопряжение дуги и прямой дугой заданного радиуса. Урок16.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение окружностей (дуг)
Внешнее сопряжение дуг окружностей
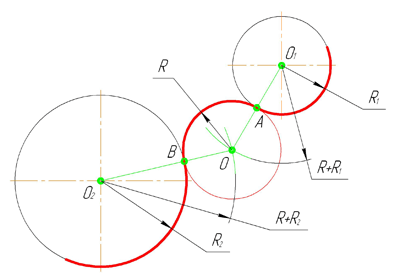
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
Внутреннее сопряжение дуг окружностей
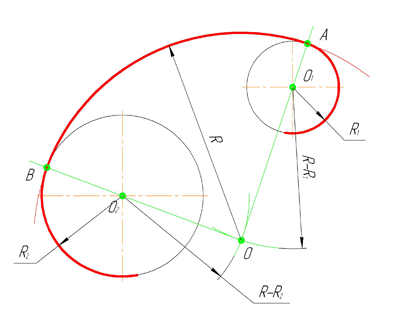
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.
Смешанное сопряжение дуг окружностей
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
Видео:Построение ВНУТРЕННЕГО СОПРЯЖЕНИЯСкачать
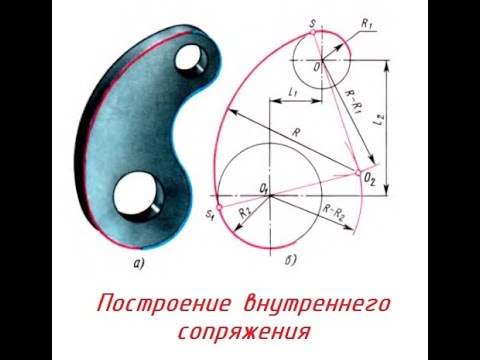
Сопряжения в инженерной графике на чертежах с примерами
Содержание:
В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.
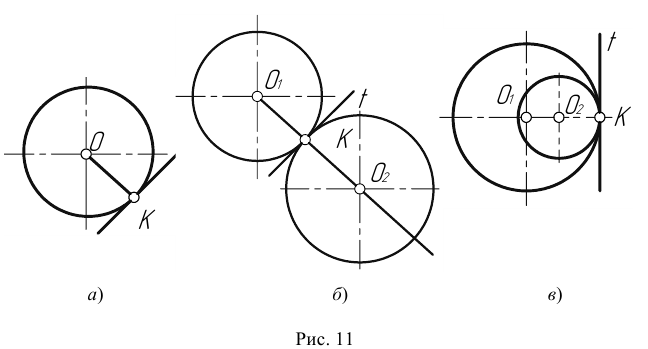
- Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
- Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).
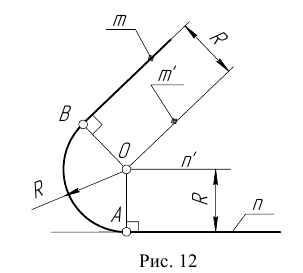
Точка касания К и центры окружностей
- Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
- Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
- Дуга сопряжения АВ – это дуга окружности, с помощью которой выполняется сопряжение (рис. 12).
- Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).
Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.
Видео:Сопряжение прямой с окружностьюСкачать

Сопряжение двух пересекающихся прямых линий
Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.
Выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от прямой n на расстояние радиуса R сопряжения. Таким множеством является прямая
параллельная данной прямой n и отстоящая от неё на расстояние R.
- Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения. Таким множеством является прямая
параллельная m и отстоящая от последней на расстояние R.
- В пересечении построенных прямых
найдем центр сопряжения О.
- Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.
Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.
Видео:Сопряжение окружностейСкачать

Сопряжения прямой с окружностью
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.
Пример 1. Пусть задана окружность радиусом R с центром в точке 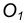
Для решения задачи выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая
параллельная m и отстоящая от неё на расстояние R.
- Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность
проведенная радиусом
- Центр сопряжения О находим как точку пересечения линий
- Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
- Проведем дугу сопряжения АВ.
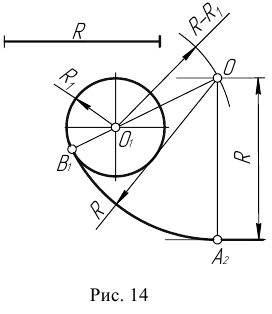
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 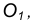
Видео:Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать

Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 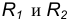
- Для нахождения центра сопряжения О проведем окружность
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
равен
- Радиусом
проведем окружность
, удаленную от данной окружности n на расстояние R.
- Найдем центр сопряжения О как точку пересечения окружностей
.
- Найдем точку сопряжения А как пересечение линии центров
с дугой m.
- Аналогично найдем точку В как пересечение линии центров
с дугой n .
- Проведем дугу сопряжения АВ.
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами 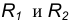
- Для нахождения центра сопряжения О проведем окружность
на расстоянии
от данной окружности m.
- Проведем окружность
на расстоянии
от данной окружности n.
- Центр сопряжения О найдем как точку пересечения окружностей
- Точку сопряжения А найдем как точку пересечения линии центров
с заданной окружностью m.
- Точку сопряжения В найдем как точку пересечения линии центров
c заданной окружностью n.
- Проведем дугу сопряжения AВ с центром в точке O.
Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.
Видео:Построение ВНЕШНЕГО СОПРЯЖЕНИЯСкачать
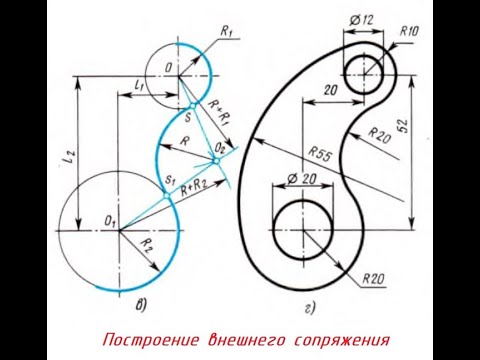
Построение касательных
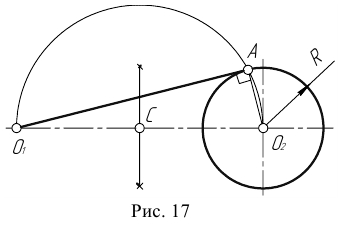
Пример 1. Дана окружность с центром в точке 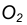
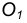
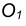
Для решения задачи выполним следующие построения.
- Соединим точку
с центром окружности
- Находим середину С отрезка
- Из точки С, как из центра, проведем вспомогательную окружность радиусом
- В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку
с точкой А.
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 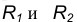
- Находим середину С отрезка
- Из точки С, как из центра, радиусом
проведем вспомогательную окружность.
- Из центра большей окружности
проведем вторую вспомогательную окружность радиусом
- Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус
идущий в точку касания В. 5. Для построения второй точки касания А проведем
- Соединим точки А и В отрезком прямой линии.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Нанесение размеров на чертежах
- Резьба на чертеже
- Соединения разъемные и неразъемные в инженерной графике
- Виды конструкторских документов
- Виды в инженерной графике
- Разрезы в инженерной графике
- Сечения в инженерной графике
- Выносные элементы в инженерной графике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Принципы построение сопряжений
При вычерчивании деталей, контуры очертаний которых состоят из прямых линий и дуг окружностей часто применяют сопряжения. Сопряжением называется плавный переход от одной линии в другую. Многие предметы имеют подобные скругления, которые делают для того, чтобы увеличить их прочность, улучшить внешний вид.
Для построения сопряжений необходимы следующие элементы: радиус, центр дуги сопряжения, точки сопряжения.
Рис. 1. Элементы сопряжения
Таблица 2. Алгоритм построения пересекающихся прямых дугой заданного радиуса
| Шаг 1. Построение центра сопряжения | ||
| Строим на расстоянии R от заданных прямых параллельные им вспомогательные прямые. Точка пересечения прямых – центр сопряжения (точка О) | ||
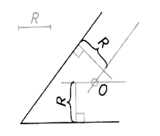 | 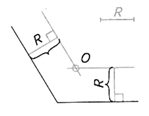 | 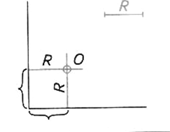 |
| Шаг 2. Построение точек сопряжения | ||
| Проводим перпендикуляры О1, О2 из центра сопряжения (точка О) к сопрягаемым прямым | ||
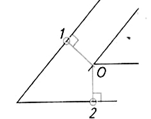 | 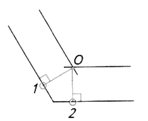 | 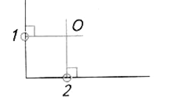 |
| Шаг 3. Построение сопрягающей дуги заданного радиуса | ||
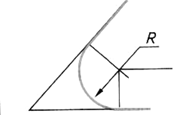 | 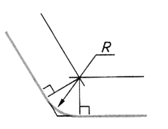 | 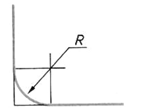 |
По окончании построения сопряжения углов вначале обводят дугу сопряжения, а затем прямые линии.
Сопряжение окружности и прямой строится по следующему алгоритму.
Таблица 3. Алгоритм построения сопряжения окружности и прямой
| Условные обозначения | Сопрягаемые элементы | |
| R – заданный радиус сопряжения между прямой и окружностью; Rвсп – вспомогательный радиусRвсп=Rокр+R; Rокр = R1– радиус окружности Точки 1 и 2 – точки сопряжения Точка О – центр сопряжения | 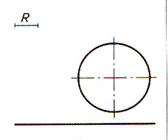 | 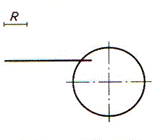 |
| Шаг 1. Построение центра сопряжения (точка О) | ||
| Строим на расстоянии Rот заданной прямой параллельную ей вспомогательную. Из центра окружности проводим вспомогательную окружность Rвсп=R1+R | 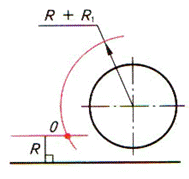 | 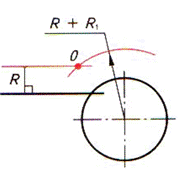 |
| Шаг 2. Построение точек сопряжения (точки 1, 2) | ||
| Опускаем перпендикуляр из точки О на заданную прямую (точка 1) и соединяем точку О с центром окружности (точка 2) | 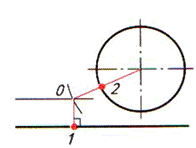 | 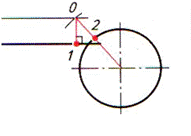 |
| Шаг 3. Построение сопрягающей дуги заданного радиуса (точка О) | ||
| Заданным радиусом R проводим дугу между точками 1 и 2 | 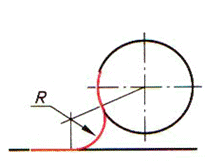 | 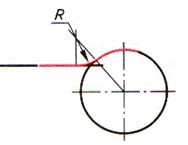 |
Сопряжение двух окружностей бывает внешним и внутренним. При внешнем сопряжении центры окружностей находятся вне сопрягающей дуги. При внутреннем — внутри сопрягающей дуги.
Таблица 4. Алгоритм построения сопряжения двух окружностей
| Внешнее сопряжение | Внутреннее сопряжение |
| Условные обозначения: R- заданный радиус сопряжения, R1- радиус большой окружности, R2 радиус малой окружности, R всп- радиус, полученный сложением или вычитанием R и R1 или R и R2 | |
| Шаг 1. Построение центра сопряжения (точка О) | |
| Строим вспомогательные дуги для внешнего сопряжения: Rвсп =R+R1 и Rвсп =R+R2 | Строим вспомогательные дуги для внутреннего сопряжения Rвсп =R-R1 и Rвсп =R-R2 |
 | 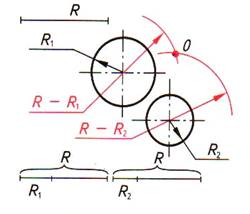 |
| Шаг 2. Построение точек сопряжения (точки 1, 2) | |
| Соединяем центр сопряжения (точка О) с центром окружностей | |
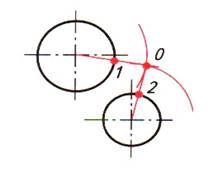 | 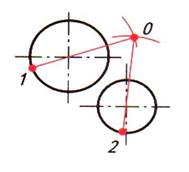 |
| Шаг 3. Построение сопрягающей дуги заданного радиуса R | |
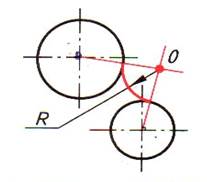 | 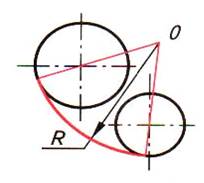 |
Контрольные вопросы и задания:
1. Что называется сопряжением?
2. Перечислить варианты сопряжений и элементы сопряжения.
ТЕМА 3. Принципы построения геометрических форм и тел на плоскости
Чертежи: проекционные, технические, машиностроительные, архитектурно-строительные выполняют только посредством параллельного прямоугольного проецирования.
1. Проецируемый предмет всегда располагают параллельно плоскости проекций;
2. Проецирующие лучи проходят через характерные точки проецируемого предмета, всегда перпендикулярно плоскости проекций.
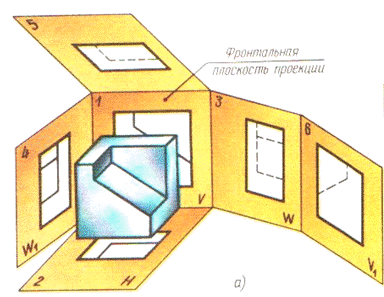
ГОСТ 2.305-68 устанавливает названия основных видов, получаемых на основных плоскостях проекций:
1- V- фронтальная (вид спереди или главный вид);
2- H – горизонтальная (вид сверху);
3- W – профильная (вид сбоку или вид слева).
Все виды на чертеже должны располагаться в проекционной связи.
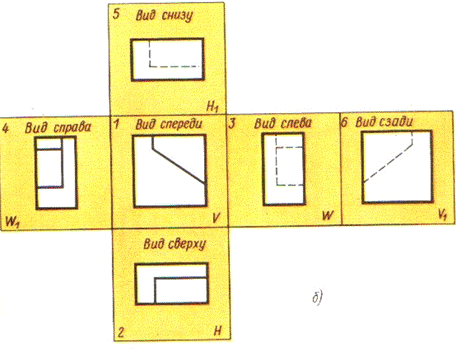
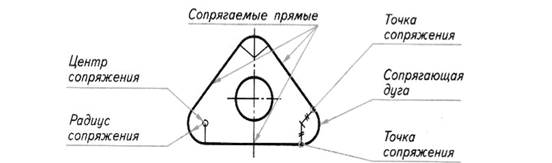
Рис. 2. Расположение проецирующих плоскостей:
а – проецирование предмета на шесть граней пустотелого куба;
б – плоскости проекций, с полученными на них изображениями.
Вид спереди (он же главный вид) располагают таким образом, чтобы вид давал наиболее полное представление о форме и размерах детали рис.3 по стрелке А.
Невидимые контуры предмета принято показывать штриховыми линиями.
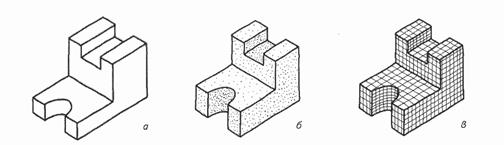
Рис.3. Ортогональная (б) и аксонометрическая (а) проекции детали
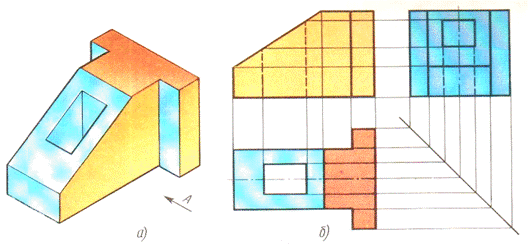
На рис.4 «а» представлено расположение видов детали с неудачным использованием поля чертежа, более рациональное расположение видов той же детали на рис. «б».
Рис. 4. Варианты расположения видов на чертеже
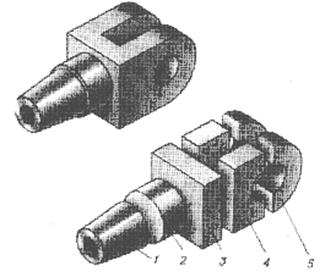
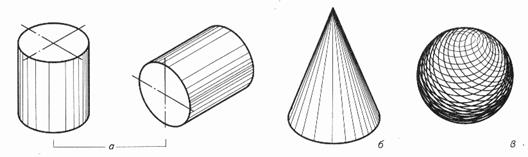
1-усеченный конус с отверстием;
2-прямой круговой цилиндр;
3-прямоугольный параллелепипед с отверстиями;
4-два прямоугольных параллелепипеда с отверстиями;
5-два полуцилиндра с отверстиями.
Для выполнения комплексных чертежей необходимо установить методы проецирования отдельных геометрических тел.
Рис. 5. Анализ формы детали
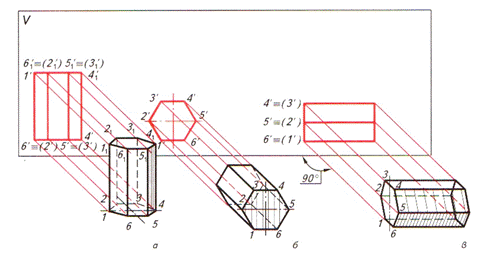
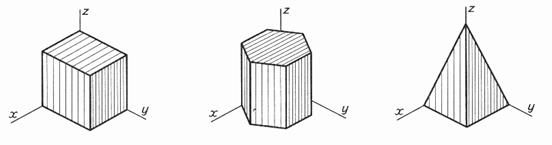
Рис. 6. Проецирование правильной шестиугольной призмы: а — вид спереди; б — вид сверху; в — вид сбоку
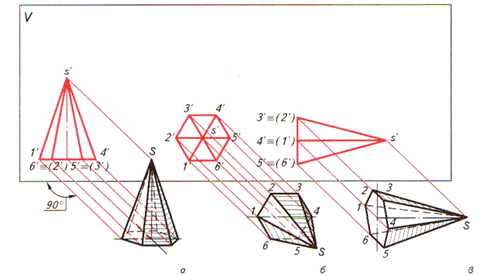
Рис.7. Проецирование правильной прямой шестиугольной пирамиды: а – вид спереди; б – вид сверху; в – вид сбоку
Тела вращения ограничены поверхностями, которые получаются в результате вращения образующей линии вокруг неподвижной оси.
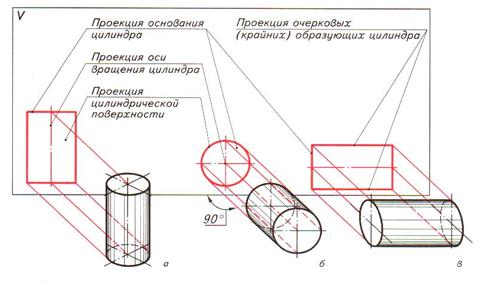
Рис. 8. Проецирование цилиндра: а – вид спереди; б – вид сверху; в – вид сбоку
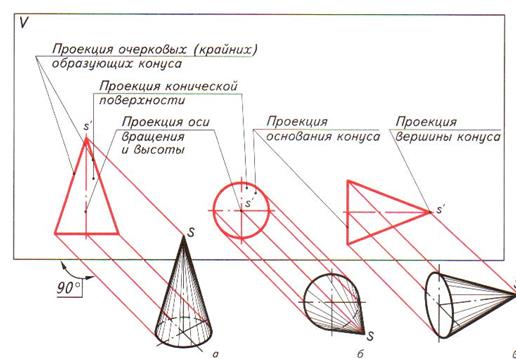
Рис.9. Проецирование конуса: а – вид спереди; б – вид сверху; в – вид сбоку
Для развития пространственного воображения полезно выполнять комплексные чертежи группы геометрических тел
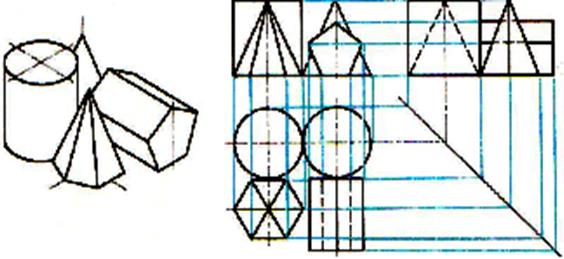
Рис.10. Композиция из геометрических тел: а – аксонометрическая проекция группы геометрических тел;
б – комплексный чертеж группы геометрических тел
Таблица 5. Алгоритм построения комплексного чертежа группы геометрических тел
| Композиция группы геометрических тел задана видом сверху. Высота цилиндра — 30 мм, высота четырехугольной призмы – 10 мм, высота шестиугольной пирамиды – 40 мм. Задание: построить комплексный чертеж группы геометрических тел. Шаг 1. Анализ состава композиции из геометрических тел. Выбор видов спереди, слева. Вычерчивание вида сверху | 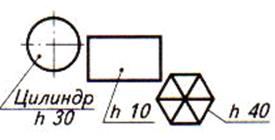 |
| Шаг 2. Поочередное построение изображения каждого геометрического тела группы на фронтальную плоскость проекций с применением линий связи | 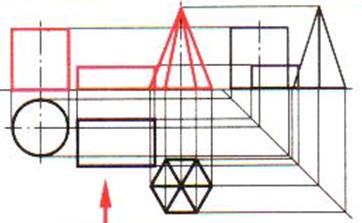 |
| Шаг 3. Поочередное построение изображения каждого геометрического тела группы на профильную плоскость проекций с применением дополнительной линии Шаг 4. Установление видимых и невидимых линий Шаг 5. Обводка чертежа | 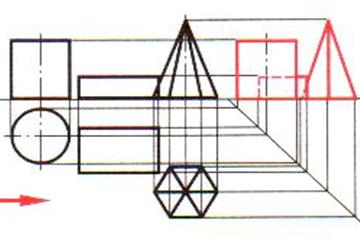 |
Контрольные вопросы и задания:
1. Что называют проецированием?
2. Назовите элементы проецирования.
3. Как получают чертеж предмета проецированием на две, три плоскости?
4. Как расположены относительно друг друга плоскости проекций, как они называются, как обозначаются?
5. Как называются оси координат? Какие размеры детали по ним откладываются?
6. Как называют изображения предмета на плоскостях V, H, W?
7. Какое изображение на чертеже основное? Как оно называется?
8. Какие геометрические тела можно задать одной, двумя проекциями?
9. Какое количество изображений предмета на чертеже можно считать необходимым и достаточным?
ТЕМА 3.1. ЭСКИЗ И ПОСЛЕДОВАТЕЛЬНОСТЬ ЕГО ВЫПОЛНЕНИЯ
Чтобы выполнить чертеж детали необходимо немало времени. Если деталь надо изготовить срочно, то ее изображение выполняют от руки и без точного соблюдения масштаба (на глаз). Чертеж детали, выполненный по правилам прямоугольного проецирования от руки называют эскизом.
В целях удобства эскиз выполняют на бумаге в клетку, совмещая осевые и контурные линии изображения с линиями сетки на бумаге.
Алгоритм выполнения эскиза и чертежа похожи:
1этап — Аналитический: анализ геометрической формы детали; выбор главного вида и рационального количества изображений; анализ габаритных размеров детали, глазомерного масштаба изображения.
2 этап — Графический: определение рабочего поля и композиции формата, проведение осей симметрии; последовательное выполнение видимых очертаний детали; последовательное изображение невидимых очертаний; нанесение на эскиз выносных и размерных линий (по длине, высоте, ширине)
3этап — Заключительный: обмер детали, нанесение размерных чисел; обводка эскиза.
ТЕМА 4. ПРИНЦИПЫ ПОСТРОЕНИЯ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
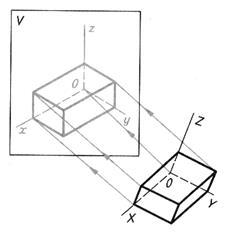
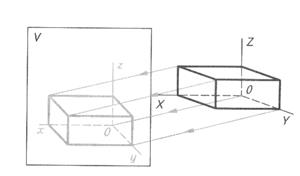
Аксонометрическая проекция – это изображение, полученное при параллельном проецировании предмета вместе с осями прямоугольных координат на какую-либо плоскость.
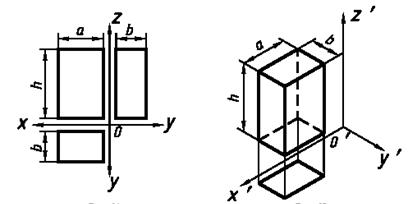
Получить аксонометрические проекции можно расположив деталь определенным образом относительно взаимно перпендикулярных координатных осей X,Y,Z и спроецировав изображение на произвольную плоскость Р называемую аксонометрической или картинной. Координатные оси X,Y,Z называют аксонометрическими осями. Направление длины детали а — параллельно оси Х, ширины b – оси Y и высоты h — оси Z.
Рис. 11. Получение аксонометрических проекций: а – комплексный чертеж параллелепипеда; б – аксонометрическая проекция параллелепипеда
Для всех аксонометрических проекций установлены общие правила:
— ось Z всегда вертикальна;
— все измерения выполняют только по аксонометрическим осям или по прямым, параллельным им;
— все прямые линии, параллельные осям координат.
Основная теорема аксонометрии впервые была сформулирована (без доказательства) немецким геометром К.Польке в 1860 г.
Три отрезка произвольной длины, лежащих в одной плоскости и выходящих из одной точки под произвольными углами, представляют собой параллельную проекцию трех равных и взаимно перпендикулярных отрезков, выходящих из одной точки в пространстве. На основании теоремы три произвольных отрезка, выходящих из одной точки на плоскости проекций, можно принять за изображение координатного трехосника с одинаковыми масштабными отрезками на его осях
Теорема Польке в 1864 г. была обобщена немецким математиком Г.Шварцем. Три отрезка произвольной длины, лежащие в одной плоскости и исходящие из общей точки под произвольными углами друг к другу, могут быть приняты за параллельную проекцию пространственного ортогонального репера (|i|=|Y|=|k|).
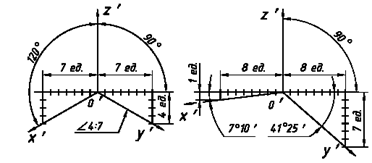
Аксонометрические проекции различают в зависимости от искажения размеров по осям координат. Коэффициентом искажения называется отношение длины проекции отрезка оси на аксонометрической плоскости к его истинной длине
Если искажение по всем осям различно, то проекции называют триметрическими; искажение по двум осям одинаковы – диметрическими; искажение по всем трем осям равно – изометрическими.
Искажение размеров в изометрической проекции равно 0,82, а в диметрической, по осям X,Y,Z соответственно: 0,94; 0,47; 0,94.
Для простоты построения принято, что в изометрии по осям показатель искажения равен 1, а в диметрии соответственно 1; 0,5; 1.
Рис. 12. Коэффициенты искажения а) изометрической проекции; б) диметрической проекции
В конструкторской документации применяют следующие виды аксонометрических проекций
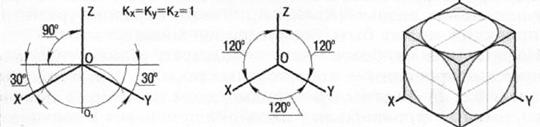
1. Прямоугольные: изометрическая и диметрическая (рис.13);
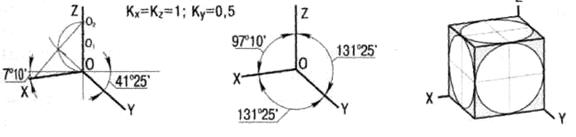
Рис. 13. Прямоугольные аксонометрические проекции: а – изометрическая; б – диметрическая
2. Косоугольные – фронтальная и горизонтальная изометрическая, фронтальная диметрическая
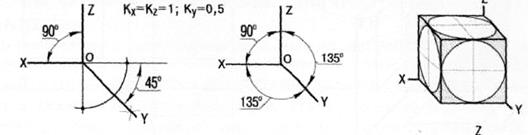
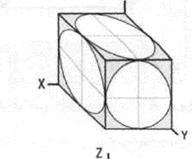
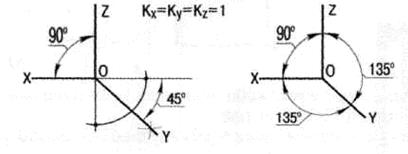
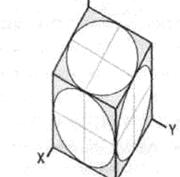

Рис.14. Косоугольные аксонометрические проекции: а – фронтальная диметрическая проекция; б – фронтальная изометрическая проекция; в – горизонтальная изометрическая проекция
Если грани предмета и координатные оси наклонить под равными углами к аксонометрической плоскости и спроецировать лучами перпендикулярными к ней, получится прямоугольная изометрическая проекция. Коротко – изометрическая проекция или изометрия (рис. 15).
Если предмет с координатными осями расположить так, чтобы оси Х и Z были параллельны аксонометрической плоскости, и спроецировать его на эту плоскость наклонными параллельными лучами, получится косоугольная фронтальная диметрическая проекция. Коротко – диметрическая проекция или диметрия (рис.16)
Рис. 15. Изометрия Рис. 16. Диметрия
Контрольные вопросы и задания:
1.Что называется аксонометрической проекцией?
2.Перечислите сходство и различие аксонометрических проекций.
Тема 4.1 Построение многоугольников в аксонометрических проекциях
Форма любого предмета – это сочетание геометрических тел. В основании каждого геометрического тела лежит определенная геометрическая фигура. Построив фигуру основания в нужной плоскости, можно легко достроить ее до геометрического тела, занимающего определенное положение в пространстве.
Рассмотрим последовательность построения многоугольников в аксонометрических плоскостях.
Таблица 6. Алгоритм построения изометрической проекции треугольника и достраивание его до призмы
| Положение фигуры | ||
| Горизонтальная плоскость проекций | Фронтальная плоскость проекций | Профильная плоскость проекций |
| Шаг 1. Анализ симметричности фигуры и ее положения относительно плоскостей проекций | ||
| Фигура имеет одну ось симметрии. Опорные точки 1 и 2 | ||
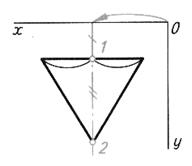 | 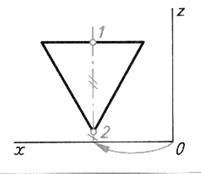 | 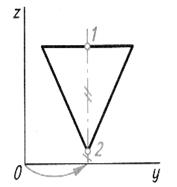 |
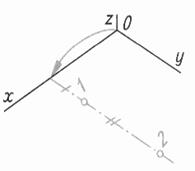
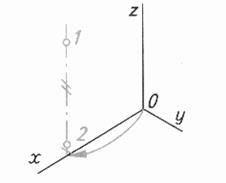
| Шаг 2. Построение осей изометрии Шаг 3. Построение оси симметрии треугольника и опорных точек 1 и 2 | ||
 |  | 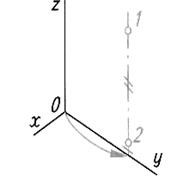 |
| Шаг 3. Построение сторон треугольника параллельно осям. Сторона проходит через точку 1 | ||
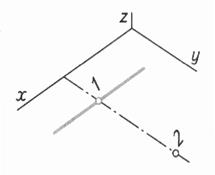 | 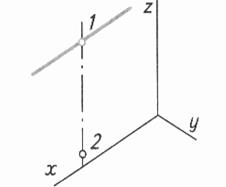 | 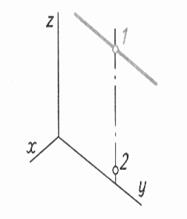 |
| Шаг 4. Построение вершин, лежащих на этой стороне | ||
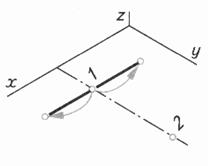 | 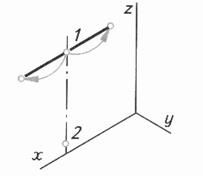 | 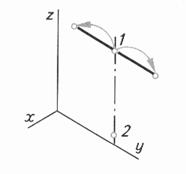 |
| Шаг 5. Последовательное соединение вершин. Достраивание треугольника до призмы Шаг 6.Определение видимости Шаг 7. Обводка | ||
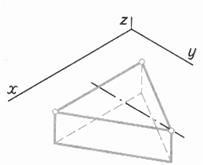 | 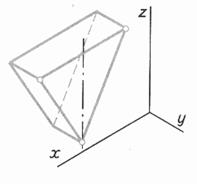 | 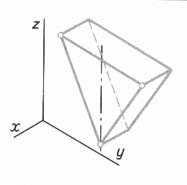 |
Алгоритм построения изометрической проекции шестиугольника приведены в таблице 7.
Таблица 7. Алгоритм построение шестиугольника и достраивание его до призмы
| Положение фигуры | ||
| Горизонтальная плоскость проекций | Фронтальная плоскость проекций | Профильная плоскость проекций |
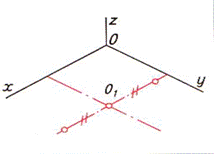
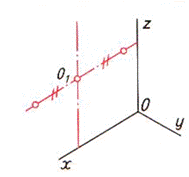
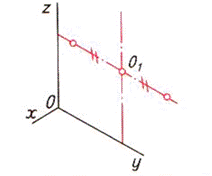
| Шаг 1. Анализ симметричности фигуры и ее положения относительно плоскостей проекций по чертежу. Фигура имеет две оси симметрии. Опорная точка — точка О1 | ||
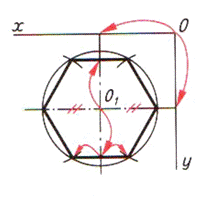 | 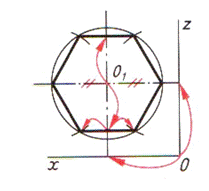 | 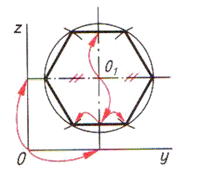 |
| Шаг 2. Построение осей изометрической проекции, ограничивающих ту плоскость, в которой лежит шестиугольник | ||
| Шаг 3. Построение осей шестиугольника и опорной точки | ||
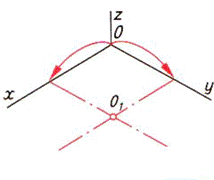 | 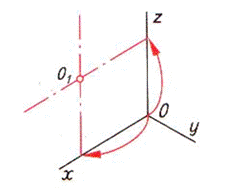 | 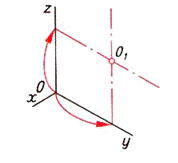 |
| Шаг 4. Построение вершин на оси симметрии | ||
 |  |  |
| Шаг 5. Построение сторон, параллельных оси симметрии | ||
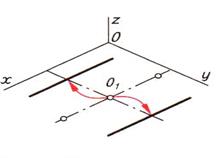 | 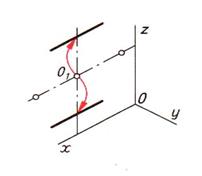 | 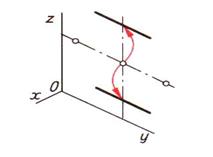 |
| Шаг 6. Построение вершин, лежащих на этих сторонах | ||
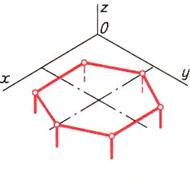 |  | 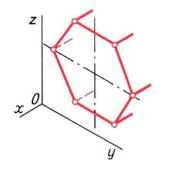 |
Построение диметрической проекции ведется в такой же последовательности, только по оси Y и параллельно ей откладываются размеры ширины элементов детали, уменьшенные в два раза.
При построении изометрической проекции окружности, лежащие в горизонтальной, фронтальной и профильной плоскостях, проецируются в эллипсы. Для упрощения построения эллипсы заменяют близкими им по очертанию овалами. Фигура, ограниченная овалом, имеет две оси симметрии. Большая и малая ось взаимно перпендикулярны. Существует несколько способов построения овалов на чертеже. Наиболее простой – вписывание овала в ромб. Сторона ромба равна диаметру изображаемой окружности (табл.8).
Таблица 8. Алгоритм построения изометрической проекции окружности
| Положение фигуры | ||
| Горизонтальная плоскость проекций | Фронтальная плоскость проекций | Профильная плоскость проекций |
| Шаг 1. Определение диаметра окружности. Построение центра окружности | ||
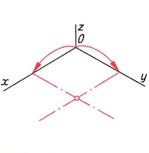 | 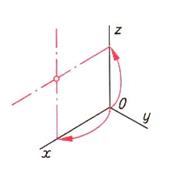 | 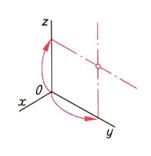 |
| Шаг 2. Построение ромба со сторонами параллельными осям | ||
 | 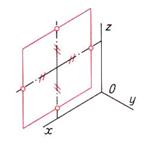 | 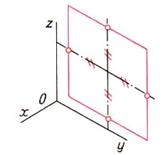 |
| Шаг 3. Построение больших дуг овала | ||
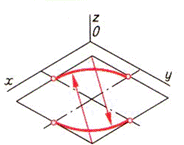 | 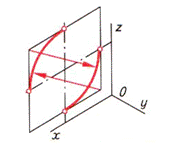 | 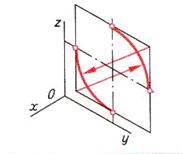 |
| Шаг 4. Построение малых дуг овалов | ||
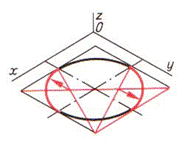 | 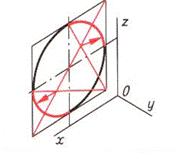 | 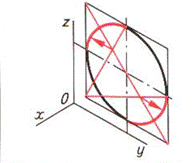 |
Если деталь получена из заготовки формы путем удаления ее отдельных частей, ее называют плоскогранной, так как все ее элементы образуют общую плоскость различной конфигурации.
Построение аксонометрической проекции объемной детали от ее нижнего основания является универсальным и используется для построения детали любой сложности.
Таблица 9. Алгоритм построения изометрической проекции плоскогранных деталей на чертеже
| Способ построения | ||
| Построение от фронтальной плоскости | Построение от профильной плоскости | |
| Шаг 1. Анализ геометрической формы детали | 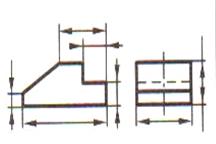 | 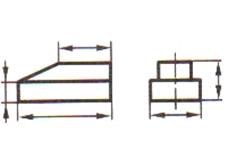 |
| Шаг 2. Построение общей грани | 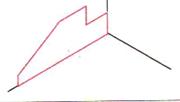 |  |
| Шаг 3. Построение ребер детали, направленных на зрителя | 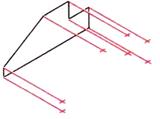 | 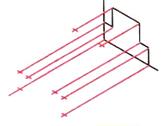 |
| Шаг 4. Построение ближней грани | 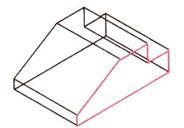 | 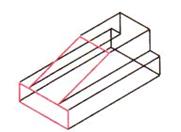 |
| Шаг 5. Установление видимости ребер и граней Шаг 6. Обводка | 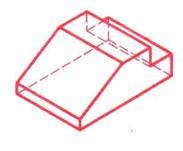 | 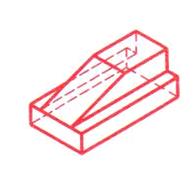 |
ТЕМА 4. 2ТЕХНИЧЕСКИЙ РИСУНОК И ПОСЛЕДОВАТЕЛЬНОСТЬ ЕГО ВЫПОЛНЕНИЯ
Изображение детали, выполненное по правилам аксонометрии от руки, с соблюдением глазомерного масштаба, называется техническим рисунком.
Технический рисунок может быть линейным
(рис. 18,а) и объемно-пространственным с передачей светотени. Показать объем детали можно штриховкой, точечным оттенением, шраффировкой (рис. 18 б, в).
Рис.17. Технический рисунок
Рис. 18. Варианты штриховки
Рис. 19. Штриховка геометрических тел
Рис.20. Штриховка тел вращения
Принято считать, что свет на деталь всегда падает сверху и слева. Разные по освещенности поверхности показывают, изменяя плотность и толщину штриховки.
На многогранниках штрихи наносят параллельно направлению аксонометрических осей (рис.19), на цилиндрических поверхностях вращения – параллельно их образующим (рис.20,а), на конических – пучком прямых, исходящих из вершины конуса (рис.20,б), на сферических – пучком дуг (рис.20,в).
ТЕМА 5.Принципы вычерчивания сечений
В технике встречаются детали, форму которых сложно передать на чертеже, представленном одним, двумя, тремя видами и даже наглядным изображением. В подобных случаях используют изображения, которые называются сечением.
Сечение – это изображение фигуры, полученной при мысленном рассечении предмета одной или несколькими плоскостями. В сечении показывают только то, что попало в секущую плоскость
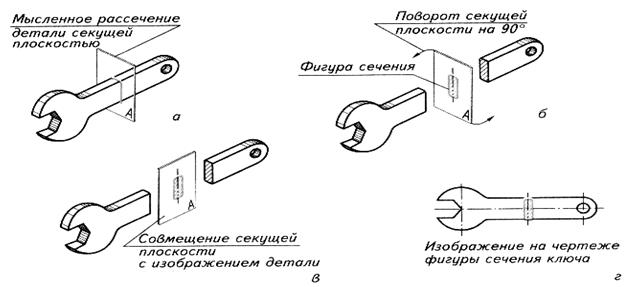
Суть сечения в следующем: часть детали, геометрическую форму которой трудно установить по чертежу, мысленно рассекают секущей плоскостью. Секущие плоскости всегда перпендикулярны к общему направлению детали или к ее оси и выявляют в конкретном месте ее поперечное или продольное строение, определяя форму фигуры сечения.
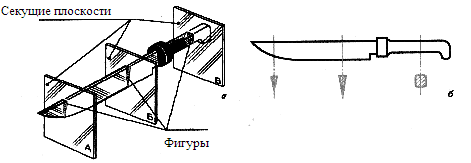
Рис.21. Сечения бытового предмета
На чертеже сечение конкретизирует геометрическую форму деталей и ее частей, раскрывая их поперечное строение. Сечения применяют когда возникает необходимость выявить форму отдельных элементов деталей, имеющих отверстия, пазы, углубления и т.д.
Рис. 22. Сечения гаечного ключа
Рассмотрим наиболее распространенные элементы точеных деталей, где чаще других применяют сечение. Их необходимо запомнить, чтобы не испытывать затруднений при чтении и выполнении чертежей.
Таблица 10. Конструктивные элементы и их изображения
| Наглядное изображение | Изображение на чертеже |
| Цилиндрическое сквозное отверстие | |
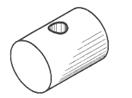 | 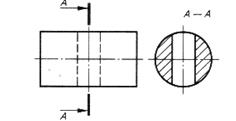 |
| Цилиндрическое сквозное отверстие с фасками | |
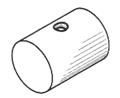 | 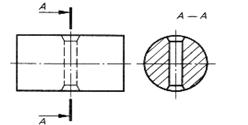 |
| Засверловка коническая | |
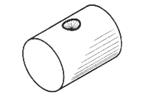 | 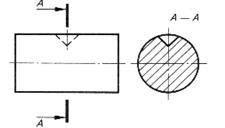 |
| Засверловка цилиндрическая (гнездо) | |
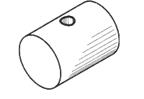 | 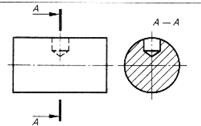 |
| Шпоночный паз (канавка) | |
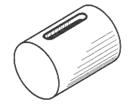 | 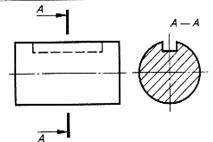 |
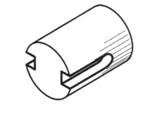 | 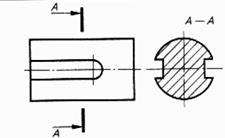 |
| Шпоночный паз для сегментной шпонки | |
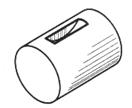 | 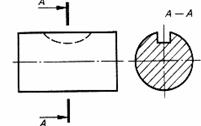 |
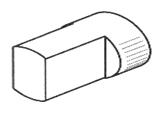
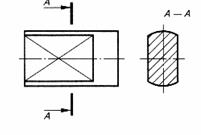
| Лыска | |
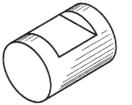 | 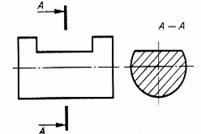 |
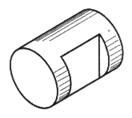 | 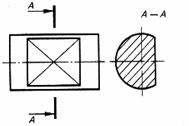 |
 |  |
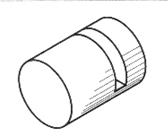
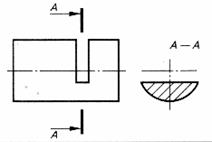
| Прорезь (паз) | |
 |  |
| Окно (паз) | |
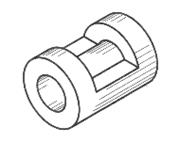 | 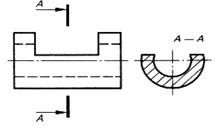 |
Чтобы по чертежу можно было легко установить, какой части детали соответствует то или иное сечение обозначается место введения секущей плоскости и фигура сечения. На рис. 23 показаны обозначения сечения.
Секущую плоскость обозначают:
-разомкнутой линией, которая не должна пересекать или касаться контура изображения детали
-указанием направления взгляда, которое передают двумя линиями, заканчивающимися стрелками
-прописными буквами русского алфавита, которые размещают с внешней стороны стрелки по отношению к детали (рис.23,в).
Фигуру сечения обозначают прописными буквами русского алфавита, аналогично обозначению секущей плоскости по типу «А-А», «Б-Б», «В-В» и т.д., расположенными горизонтально над фигурой сечения
Рис. 23 Обозначение сечений
В зависимости от положения сечения относительно изображения детали рассматривают два типа сечения: наложенное (рис.24) и вынесенное (рис.25).
Рис.24. Наложенное сечение
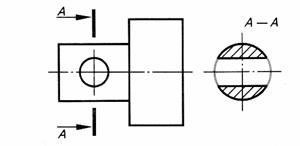
Рис.25. Вынесенное сечение
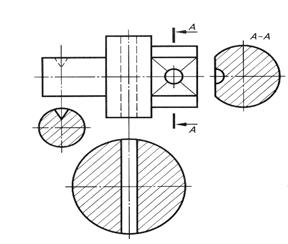
Если секущая плоскость проходит так, что сечение распадается на несколько частей, сечение не выполняется.
Рис. 26. Сечение, расположенное на оси симметрии
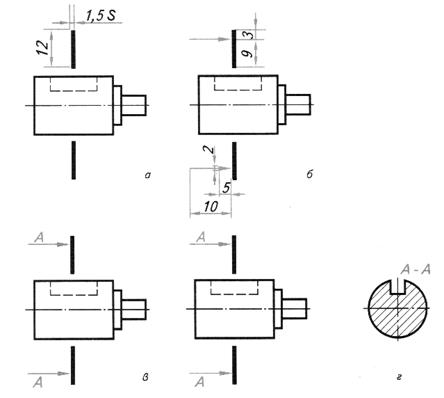
Таблица 11. Алгоритм построения сечения
| Шаг 1. Анализ геометрической формы детали | |
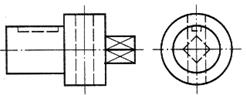 | Деталь представляет собой сочетание двух соосно расположенных цилиндров и четырехугольной призмы правильной формы. В цилиндре меньшего диаметра — шпоночный паз. В цилиндре большего диаметра – сквозное цилиндрическое отверстие |
| Шаг 2. Выбор места введения секущей плоскости | |
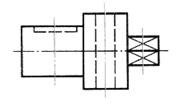 | Первая секущая плоскость проходит через шпоночный паз, вторая — через центр цилиндрического отверстия, третья — через призму |
| Шаг 3. Мысленно представление фигур сечения | |
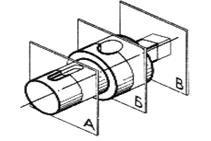 | Первое сечение – круг с прямоугольным вырезом. Второе сечение – круг с вырезом вдоль вертикальной оси. Третье сечение – квадрат |
| Шаг 4. Построение фигур сечения | |
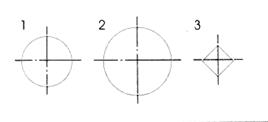 | Построение общего очертания фигур 1, 2, 3 |
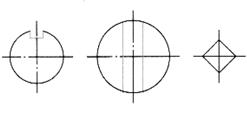 | Построение конструктивного элемента, попавшего в сечение |
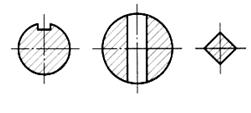 | Штриховка фигуры сечения |
| Шаг 5. Обозначение секущих плоскостей и фигур сечений. Обводка | |
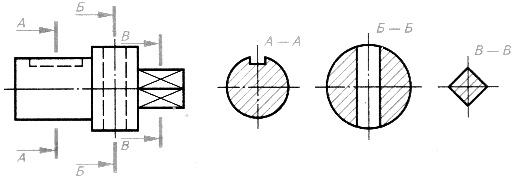 |
Контрольные вопросы и задания:
1. С какой целью применяют сечения?
2. Какие типы сечений установлены ГОСТом?
3. Как на чертеже может быть показана линия сечения?
4. Как обозначаются наложенные и вынесенные сечения?
5. В каких случаях вынесенные сечения не обозначаются?
6. Как обводят линии контура наложенного и вынесенного сечений?
ТЕМА 6. Принципы вычерчивания разрезов
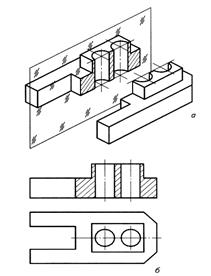
Разрез – изображение предмета, мысленно рассеченного одной или несколькими плоскостями. На разрезе показывают то, что попало в секущую плоскость и то, что за ней.
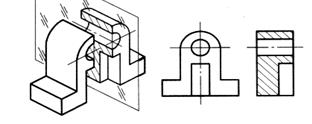
Если секущая плоскость параллельна фронтальной плоскости проекций, то вертикальный разрез называется фронтальным и размещается на месте главного вида (рис.27).
Рис.27. Образование простого фронтального разреза
При секущей плоскости, параллельной профильной плоскости проекций, вертикальный разрез называется профильным и располагается на месте вида слева (рис.28).
Рис.28. Образование простого профильного разреза
Если секущая плоскость параллельна горизонтальной плоскости проекций, такой разрез называется горизонтальным и выполняется на месте вида сверху (рис.29)
Рис.29. Образование простого горизонтального разреза
Разрезы, как и сечения, используют для увеличения наглядности чертежа, облегчения его чтения, так как при их использовании значительно сокращается количество линий невидимого контура.
Если разрезы находятся в проекционных связях с видами, разрезы на чертежах не обозначают. Если же секущая плоскость разреза не совпадает с плоскостью симметрии детали, разрезы обозначают также как сечения: разомкнутой линией показывают место рассечения детали, стрелками поясняют направление взгляда и прописными буквами русского алфавита обозначают разрез. Буквы не зависимо от положения стрелок, всегда вертикальны.
Любой простой разрез выполняют в определенной последовательности. Рассмотрим алгоритм его построения на примере фронтального разреза (табл.12)
Таблица 12 — Алгоритм построения фронтального разреза
| Шаг 1.Анализ геометрической формы детали и определение ее симметричности | |
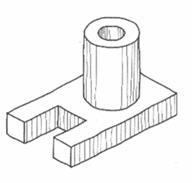
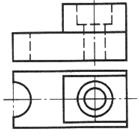 | В основании детали параллелепипед, на верхней грани которого расположен параллелепипед меньшего размера. На высоту этих параллелепипедов проходит сквозное отверстие, образованное двумя соосно расположенными цилиндрами. В левом торце большего параллелепипеда – полуцилиндрический вырез (паз). Деталь имеет одну плоскость симметрии |
| Шаг 2. Выявление элементов детали, подлежащих разрезу | |
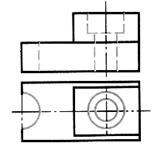 | Необходимо выявить невидимые элементы: соосно расположенные цилиндры и полуцилиндрический паз |
| Шаг 3. Определение направления и место секущей плоскости | |
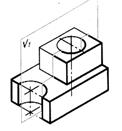 | Секущая плоскость пройдет параллельно фронтальной плоскости проекций и совпадет с плоскостью симметрии детали, следовательно, разрез не обозначается |
| Шаг 4. Представление фигуры сечения | |
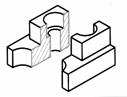 | Фигура сечения состоит из двух частей |
| Шаг 5. Ликвидация линий видимого контура | |
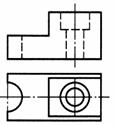 | Убирается линия, соответствующая нижнему основанию меньшего параллелепипеда и принадлежащая мысленно удаляемой части детали |
| Шаг 6. Преобразование линий невидимого контура (элементов детали, попавших в разрез) в видимые | |
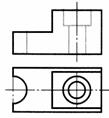 | Штриховые линии, изображающие невидимые элементы детали (соосно расположенные цилиндры, полуцилиндрический паз), заменяем сплошными линиями видимого контура |
| Шаг 7. Штриховка фигуры сечения. Обводка | |
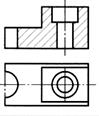 | Штриховка выполняется сплошными тонкими линиями толщиной s/3 под углом 45° к линии рамки чертежа. Обводим получившиеся изображения сплошной основной линией |
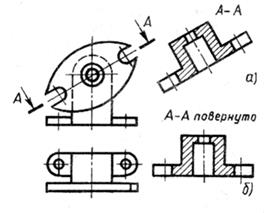
Разрез строят и располагают в соответствии с направлением взгляда, указанным стрелками на линии сечения.
Наклонный разрез допускается располагать в любом месте чертежа (рис. 30, а), а также с поворотом до положения, соответствующего принятому для данного предмета на главном изображении. В последнем случае добавляют слово «повернуто» (рис. 30,б).
Такие элементы деталей, как спицы, ребра жесткости, тонкие стенки и стандартные детали на разрезах показывают незаштрихованными.
Рис. 30. Изображение и обозначение наклонного разреза
ТЕМА 6.1Сложные разрезы
Сложными называются разрезы, полученные при помощи нескольких секущих плоскостей. Сложные разрезы подразделяют на ступенчатые и ломаные.
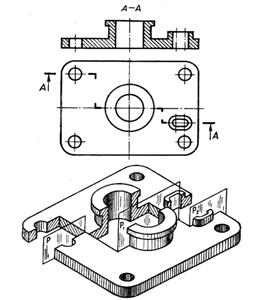
Каждая секущая плоскость выявляет внутреннюю форму детали на своем участке. Сечения, полученные тремя плоскостями, совмещают в одну плоскость чертежа. Границу между сечениями при этом не показывают.
Ломаным называется разрез, полученный при рассечении взаимно пересекающимися плоскостями. Особенность выполнения разреза состоит в том, что одну из секущих плоскостей с фигурой сечения поворачивают вокруг линии пересечения плоскостей до совмещения с другой секущей плоскостью, параллельной какой-либо из основных плоскостей проекций, и только после этого обе фигуры сечения совмещают с плоскостью чертежа. Направление поворота секущей плоскости может не совпадать с направлением взгляда (рис. 32), указанным стрелками на линиях сечения.
Рис.31. Ступенчатый разрез
При повороте секущей плоскости элементы детали, расположенные за ней, не перемещают: их изображают так, как они проецируются на соответствующую плоскость, с которой производится совмещение.
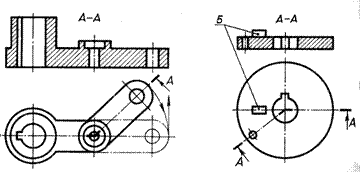
Рис.32. Ломаный разрез
ТЕМА 6.2СОЕДИНЕНИЕ ВИДА И РАЗРЕЗА
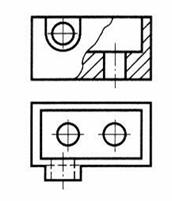
Невидимые линии на части (половине) вида не наносят.
Если ось симметрии детали вертикальна, то половину разреза всегда изображают справа, а половину вида слева от нее.
Если ось симметрии детали горизонтальна, то половину разреза изображают под горизонтальной осью симметрии. А половину вида – над ней.
Невидимые линии на части (половине) вида не показывают
Рис. 33. Соединение части вида и части разреза
Если ребро расположено на наружной поверхности, то показывают больше половины вида (рис. 34, б).
Границей, разделяющей половину вида и половину разреза, является ось симметрии – штрихпунктирная линия. Границей, разделяющей часть вида и часть разреза, является — тонкая сплошная волнистая линия.
Рис. 34. Соединение части вида и части разреза при совпадении проекции ребра с осью симметрии:
а – ребро расположено на внутренней поверхности; б – ребро расположено на наружной поверхности
При соединении половины вида и половины разреза размеры наносят следующим образом:
-размеры, относящиеся к внутреннему строению детали, располагают со стороны разреза;
-размеры, относящиеся к наружному строению детали – со стороны вида;
-размеры элементов детали, попавших в разрез, указывают размерной линией, имеющей стрелку на одном конце и заходящей за ось симметрии другим концом на 2…5 мм. Знак диаметра наносят ближе к оси симметрии.
Рис. 35. Простановка размеров на соединении половина вида с половиной разреза
Контрольные вопросы и задания:
1. В каком случае можно соединить половину вида с половиной разреза?
2. Какой тип линии применяется для разграничения половины вида и половины разреза и для разграничения части вида и части разреза?
Построение соединения половины вида и половины разреза на чертеже выполняют по алгоритму, приведенному в таблице 13.
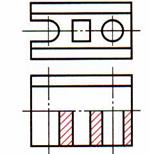
Таблица 13. Алгоритм построения соединения половины вида и половины разреза
| Вертикальная ось симметрии | Горизонтальная ось симметрии |
| Шаг 1. Анализ геометрической формы детали и определение ее симметричности | |
| Шаг 2. Выявление элементов, подлежащих разрезу | |
| Шаг 3.Определение направления и места секущей плоскости | |
| Шаг 4. Мысленное представление фигур сечения | |
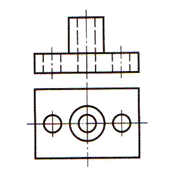 | 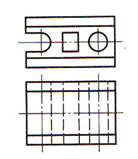 |
| Шаг 5. Удаление линий видимого контура, относящихся к мысленно удаляемой части детали; преобразование линий невидимого контура в видимый справа от вертикальной и снизу от горизонтальной оси симметрии детали | |
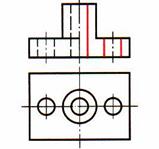 | 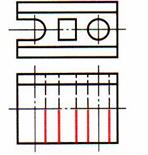 |
| Шаг 6. Удаление линий невидимого контура слева от вертикальной и сверху от горизонтальной оси симметрии | |
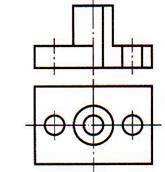 |  |
| Шаг 7. Штриховка фигур сечения, проверка, обводка | |
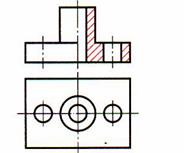 |  |
ТЕМА 6.3РАЗРЕЗ В АКСОНОМЕТРИИ
Для наглядности изображения рекомендуется использовать разрез в аксонометрии. В результате на наглядном изображении получается вырез части детали, который позволяет увидеть и внутреннее, и внешнее ее строение.
Используют две плоскости, их располагают параллельно координатным плоскостям и направляют вдоль осей симметрии. Разрез в аксонометрии выполняют по алгоритму, как в таблице 14.
Таблица 14. Алгоритм построения разреза в аксонометрической проекции
| Шаг 1. Анализ геометрической формы детали | 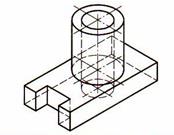 |
| Шаг 2. Выбор места для введения секущих плоскостей | |
| Шаг 3. Построение фигур сечения | 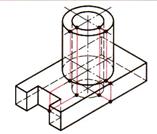 |
| Шаг 4. Обозначение линий видимого контура | 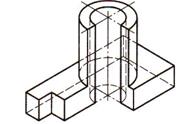 |
| Шаг 5. Преобразование линий невидимого контура в видимые и удаление остальных линий невидимого контура | 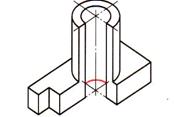 |
| Шаг 6. Штриховка фигур сечения, проверка, обводка чертежа | 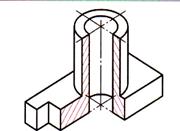 |
ТЕМА 6.4ВЫПОЛНЕНИЕ РАЗРЕЗОВ НА ЭСКИЗАХ И ТЕХНИЧЕСКИХ РИСУНКАХ
При выполнении эскизов и технических рисунков сложных деталей для выявления их внутренней формы также используют разрезы. Рассмотрим алгоритм выполнения эскиза детали с необходимыми разрезами.
Таблица 15. Алгоритм выполнения эскиза детали с необходимыми разрезами
| Шаг 1. Анализ геометрической формы детали и определение ее симметричности | |
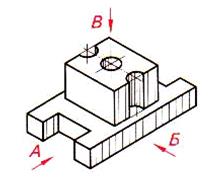 | Деталь представляет собой сочетание двух прямоугольных параллелепипедов, поставленных один на другой. Через всю высоту детали проходит сквозное цилиндрическое отверстие. В верхнем параллелепипеде выполнены два полуцилиндрических, а в нижнем – два призматических выреза |
| Шаг 2. Установление количества и характера изображений | |
| Главный вид детали – по стрелке Б. Чтобы выявить форму детали необходимо выполнить три изображения: -соединение половины главного вида с половиной фронтального разреза; -вид сверху; -соединение половины вида слева с половиной профильного разреза | |
| Шаг 3. Анализ графического состава изображений и их симметричности | |
| Шаг 4. Выполнение эскиза | |
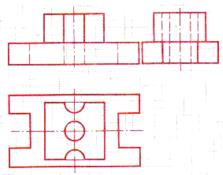 | Изображение габаритных прямоугольников в пропорциональном масштабе. Построение видимых очертаний детали. Построение невидимых очертаний детали |
| Шаг 5. Выполнение разрезов | |
| Соединение половины главного вида с половиной фронтального разреза: -удаление на правой части изображения линий видимого контура, относящихся к мысленно удаляемой части детали; -преобразование линий невидимого контура в видимые справа от оси симметрии; -удаление линий невидимого контура слева от оси симметрии; -нанесение штриховки на фигуре сечения. Соединение половины вида слева с половиной профильного разреза (построение аналогичное) | |
| Шаг 6. Нанесение выносных и размерных линий | |
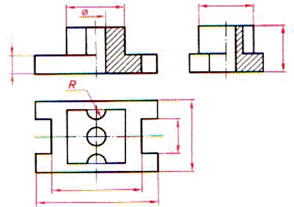 | По длине детали: -размеры элементов; -координирующие размеры; -габаритные размеры. По высоте и по ширине детали – в той же последовательности |
| Шаг 7. Обмер детали и нанесение размеров | 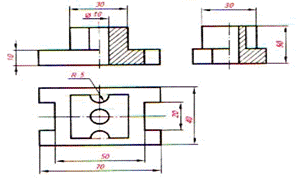 |
| Шаг 8. Обводка эскиза (выполняется карандашом от руки) |

Рис. 36. Технический рисунок с ¼ частью выреза
Контрольные вопросы и задания:
1. Что такое разрез? Для какой цели применяют разрезы?
2. Как принято обозначать разрезы?
3. Как подразделяются разрезы в зависимости от положения секущей плоскости?
4. Какие разрезы называются простыми? Как обозначают простые разрезы?
5. Что такое сложный разрез?
6. Какие разрезы называют ступенчатыми? ломаными? наклонными?
7. Что такое «местный» разрез?
8. Как проводят секущие плоскости при образовании разрезов на аксонометрических изображениях?
9. Как определяется направление линии штриховки сечений в аксонометрических изображениях?
10. Что общего у сечения и разреза?
11. Какие элементы детали, попавшие в секущую плоскость, не заштриховывают?
ТЕМА 7.ПРИНЦИПЫ ПОСТРОЕНИЯ РАЗВЕРТОК
Развертки широко пользуют при изготовлении изделий из листовых материалов.
Разверткой поверхности геометрического тела называют фигуру, которая получается в результате совмещения всех граней или всех поверхностей, ограничивающих тело, с одной плоскостью.
Рис.37. Развертка детали
Рассмотрим построение разверток некоторых геометрических тел.

Рис.38. Развертка призмы: а – вид призмы спереди и вид сверху; б – развертка призмы

Рис. 39. Развертка четырехугольной пирамиды: а – вид пирамиды спереди и сверху; б – развертка пирамиды

Рис.40. Развертка цилиндра: а – вид цилиндра спереди и сверху; б – развертка цилиндра
Развертка конуса. Построим развертку прямого кругового конуса. Боковая поверхность конуса на развертке представляет собой круговой сектор, радиус которого равен длине образующей конуса l.
Для построения развертки графическим путем разделим окружность основания на 12 равных частей и отложим на развертке конуса 12 хорд вдоль дуги, проведенной ранее радиусом l. Первую и последнюю точки соединим с точкой S. Получим развертку боковой поверхности конуса, затем к ней причерчено снование.
Поверхности некоторых криволинейных тел, например, шара, тора нельзя развернуть в одну плоскость. Для этого используют способы приближенной развертки.
Рис.41. Развертка конуса: а – вид конуса спереди и сверху; б – развертка конуса
ТЕМА 8.ПРИНЦИПЫ ВЫЧЕРЧИВАНИЯ РАЗЪЕМНЫХ И НЕРАЗЪЕМНЫХ СОЕДИНЕНИЙ
Чертеж любого соединения выполняют по определенным правилам, установленным государственным стандартом. ГОСТом определены форма, размеры и условные обозначения деталей, входящих в соединение. Это дает возможность их взаимозаменяемости.
Рис. 42. Классификация соединений

Рис.43. Профили резьбы: а — треугольный, б — трапецеидальный, в — круглый, г — прямоугольный
У каждой резьбы различают: наружный большой диаметр — d, внутренний меньший диаметр — d1, шаг резьбы — Р(расстояние между двумя соседними выступами).

Резьбу на чертежах не рисуют такой, какой мы ее видим, а изображают условно. Вместо вершин профиля проводят
Дата добавления: 2019-04-03 ; просмотров: 10201 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
📹 Видео
Геометрическое черчение. Построение дуги сопряжения окружности и прямойСкачать

СопряжениеСкачать

Сопряжение острого углаСкачать
Инженерная графика. 2 урок. Построение сопряженийСкачать

Сопряжение прямого углаСкачать

Сопряжение прямой и окружностиСкачать
ВСЯ СУТЬ СОПРЯЖЕНИЙ И ПЕРЕХОДОВ. Правило построения сопряжений. Геометрические построенияСкачать

Построение сопряжения двух прямых, прямой и окружностиСкачать

Сопряжения. Способы построение сопряженияСкачать

Внутреннее сопряжение дуги и прямой дугой заданного радиуса.Урок17.(Часть1.ГЕОМЕТРИЧЕСКИЕПОСТРОЕНИЯ)Скачать

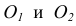
 параллельная данной прямой n и отстоящая от неё на расстояние R.
параллельная данной прямой n и отстоящая от неё на расстояние R.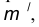 параллельная m и отстоящая от последней на расстояние R.
параллельная m и отстоящая от последней на расстояние R.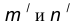 найдем центр сопряжения О.
найдем центр сопряжения О.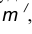 параллельная m и отстоящая от неё на расстояние R.
параллельная m и отстоящая от неё на расстояние R.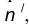 проведенная радиусом
проведенная радиусом 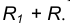
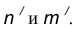
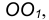 т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.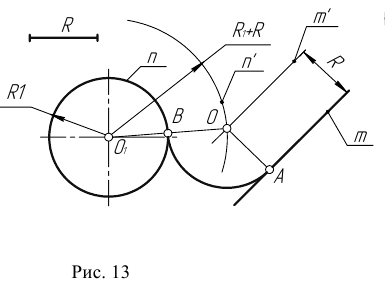
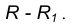
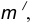 удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности 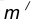 равен
равен 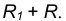
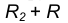 проведем окружность
проведем окружность 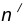 , удаленную от данной окружности n на расстояние R.
, удаленную от данной окружности n на расстояние R.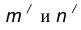 .
.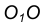 с дугой m.
с дугой m.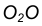 с дугой n .
с дугой n .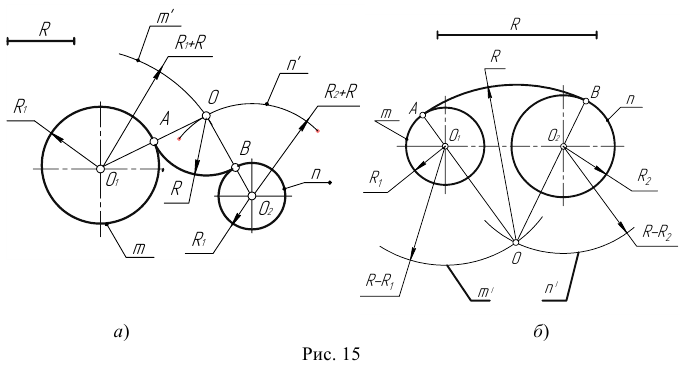
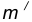 на расстоянии
на расстоянии 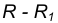 от данной окружности m.
от данной окружности m.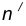 на расстоянии
на расстоянии 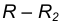 от данной окружности n.
от данной окружности n.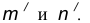
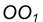 с заданной окружностью m.
с заданной окружностью m.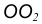 c заданной окружностью n.
c заданной окружностью n.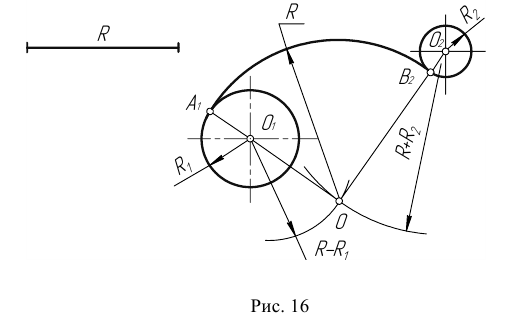
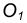 с центром окружности
с центром окружности 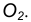
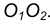
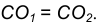
 с точкой А.
с точкой А.
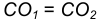 проведем вспомогательную окружность.
проведем вспомогательную окружность.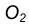 проведем вторую вспомогательную окружность радиусом
проведем вторую вспомогательную окружность радиусом 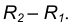
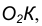 идущий в точку касания В. 5. Для построения второй точки касания А проведем
идущий в точку касания В. 5. Для построения второй точки касания А проведем