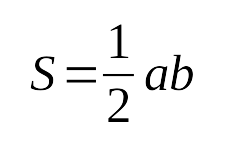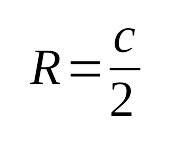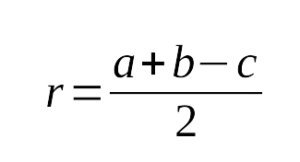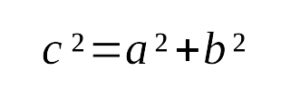Аксиомы по прямоугольным треугольникам

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Определение

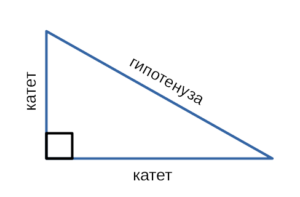
Прямоугольный треугольник — это треугольник, в котором один из углов прямой.

Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.

Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.

Видео:7 класс, 27 урок, Об аксиомах геометрииСкачать

Свойства прямоугольного треугольника

В прямоугольном треугольнике:

1. Сумма острых углов 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
3. Медиана, проведенная к гипотенузе, равна ее половине.
4. Центр описанной окружности — середина гипотенузы.
   

Формулы:

1. Площадь прямоугольного треугольника равна
   половине произведения катетов:
   
2. Радиус описанной окружности около прямоугольного
   треугольника равен половине гипотенузы:
   
3. Радиус вписанной окружности в прямоугольный треугольник
   выражается следующим образом:
   
4. Квадрат гипотенузы равен сумме квадратов катетов:

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Признаки равенства прямоугольных треугольников

С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.

1. По двум катетам:
   Если два катета одного прямоугольного треугольника соответственно
   равны двум катетам другого прямоугольного треугольника,
   то такие треугольники равны.
   
2. По катету и гипотенузе:
   Если катет и гипотенуза одного прямоугольного треугольника соответственно
   равны катету и гипотенузе другого прямоугольного треугольника,
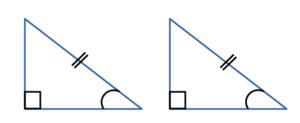
   то такие треугольники равны.
   
3. По гипотенузе и острому углу:
   Если гипотенуза и острый угол одного прямоугольного треугольника соответственно
   равны гипотенузе и острому углу другого прямоугольного треугольника,
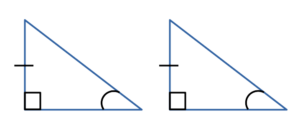
   то такие треугольникиравны.
   
4. По катету и острому углу:
   Если катет и острый угол одного прямоугольного треугольника соответственно
   равны катету и острому углу другого прямоугольного треугольника,
   то такие треугольники равны.

Видео:Высота прямоугольного треугольникаСкачать

Признаки прямоугольного треугольника

С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.

1. По теореме Пифагора:
   Если квадрат стороны равен сумме квадратов двух других сторон,
   то треугольник прямоугольный.
2. По центру описанной окружности:
   Если центр описанной окружности лежит на стороне треугольника,
   то треугольник прямоугольный.
3. По медиане:
   Если медиана треугольника равна половине стороны, к которой она проведена,
   то треугольник прямоугольный.
4. По площади:
   Если площадь треугольника равна половине произведения двух его сторон,
   то треугольник прямоугольный.
5. По радиусу описанной окружности:
   Если радиус описанной окружности равен половине,
   то треугольник прямоугольный.

Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Признаки подобия прямоугольных треугольников

С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.

Видео:прямоугольный треугольник для ЕГЭ #егэ2023 #математика #математикаегэ #школа #fyp #егэСкачать

Прямоугольный треугольник

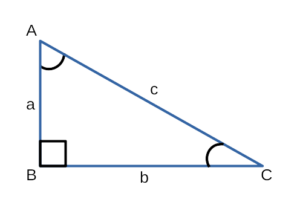
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Аксиомы по прямоугольным треугольникам

Прямоугольный треугольник — треугольник, имеющий прямой угол. Стороны, образующие прямой угол, называют катетами, а сторону, противолежащую к прямому углу, называют гипотенузой.

Свойства прямоугольного треугольника:
1. Катет меньше гипотенузы.
2. Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора): с 2 = а 2 + b 2 .
3. Сумма острых углов прямоугольного треугольника равна 90°.
4. Медиана,проведенная к гипотенузе,равна половине гипотенузы (радиусу окружности, описанной около треугольника).
5. Радиус окружности, вписанной в прямоугольный треугольник ,можно вычислить по формуле: r = (a + b — c)/2.
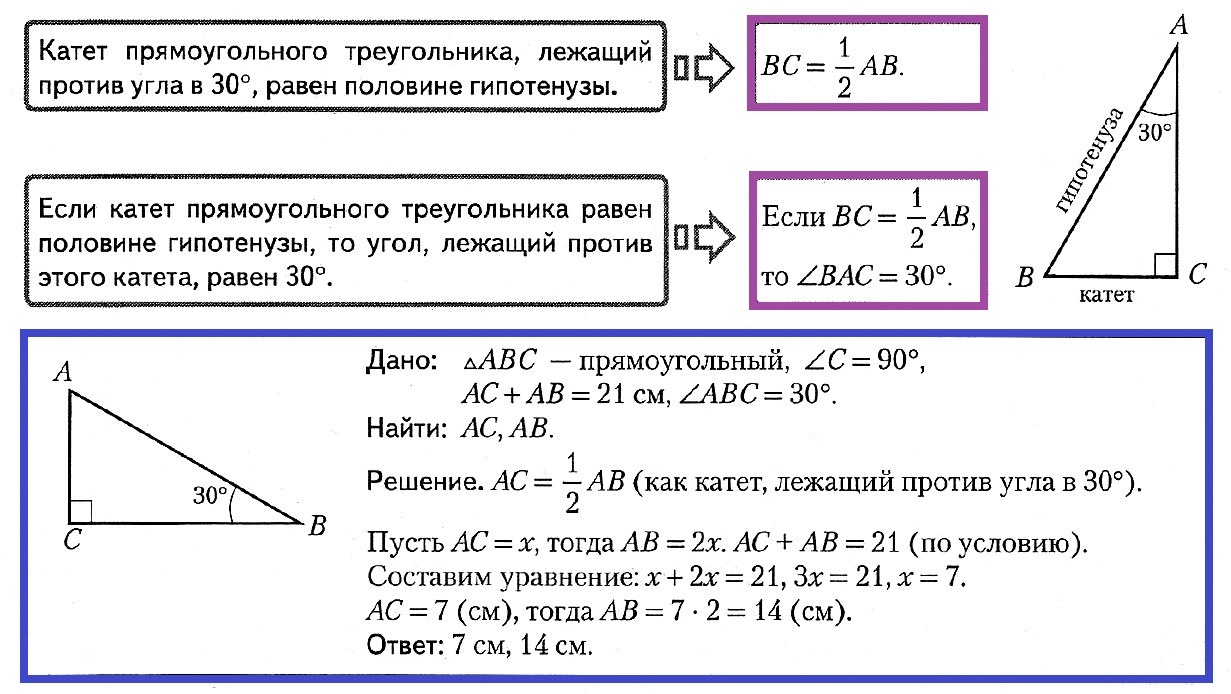
6. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
7. Если катет прямоугольного треугольника равен 1/2 гипотенузы, то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

Два прямоугольных треугольника равны если:
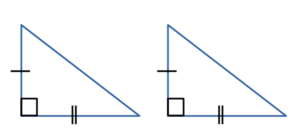
• два катета одного треугольника равны двум катетам другого;
• катет и острый угол одного треугольника равны катету и острому углу другого треугольника;
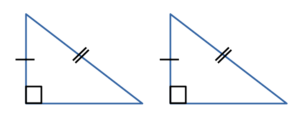
• гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого треугольника;
• гипотенуза и катет одного треугольника равны гипотенузе и катету другого треугольника.

Это конспект по теме «Прямоугольные треугольники». Выберите дальнейшие действия:

🎥 Видео

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Основные теоремы и аксиомы геометрии.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Свойства прямоугольного треугольника. Практическая часть. 7 класс.Скачать

ПРОДОЛЖАЕМ РАЗБИРАТЬСЯ С ПРЯМОУГОЛЬНЫМ ТРЕУГОЛЬНИКОМ ЧАСТЬ II #Shorts #математика #егэ #огэСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Что с углами. Прямоугольный треугольник #shortsСкачать

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Высота в прямоугольном треугольникеСкачать

Медиана в прямоугольном треугольникеСкачать