О чем эта статья:
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Прямоугольная декартова система координат
Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
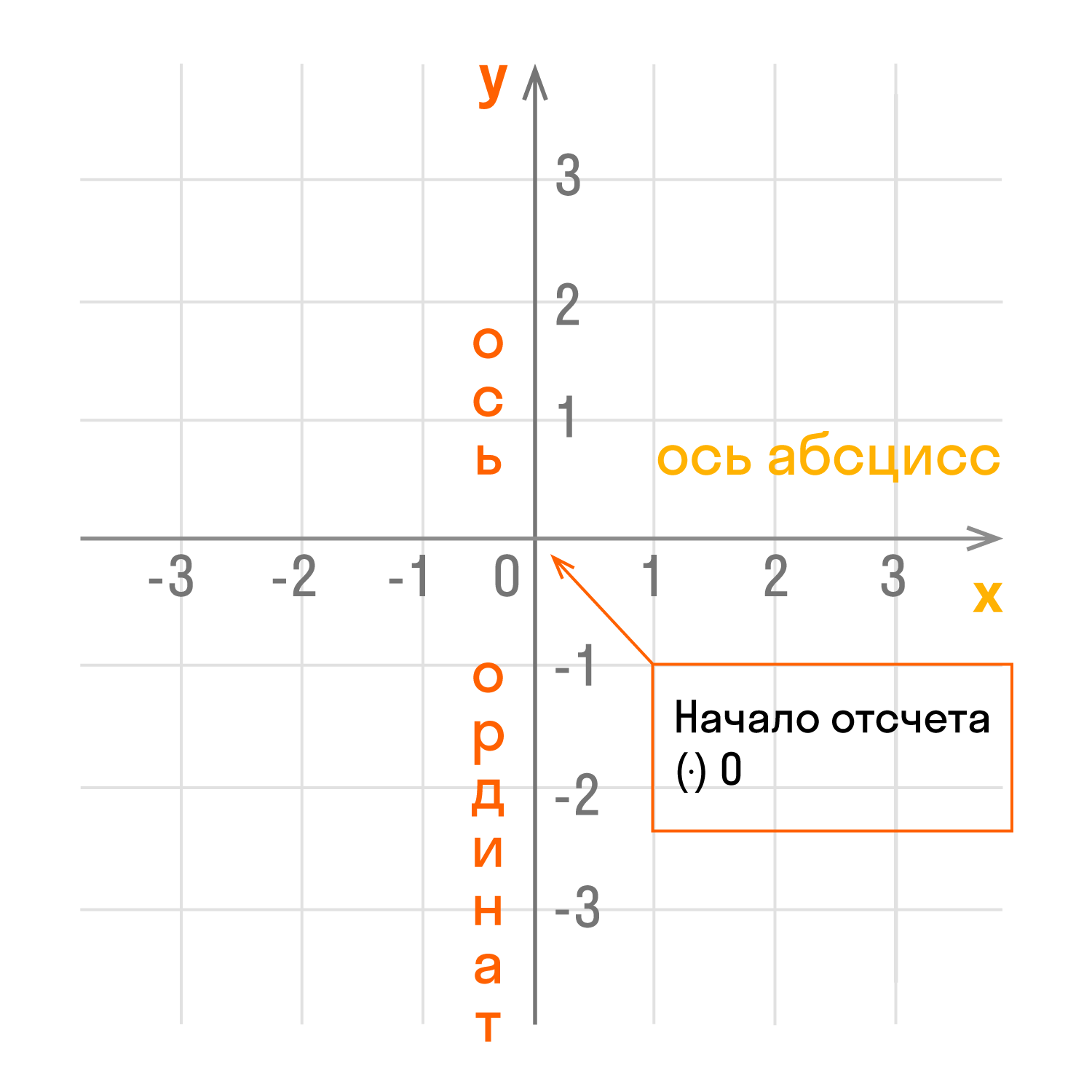
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
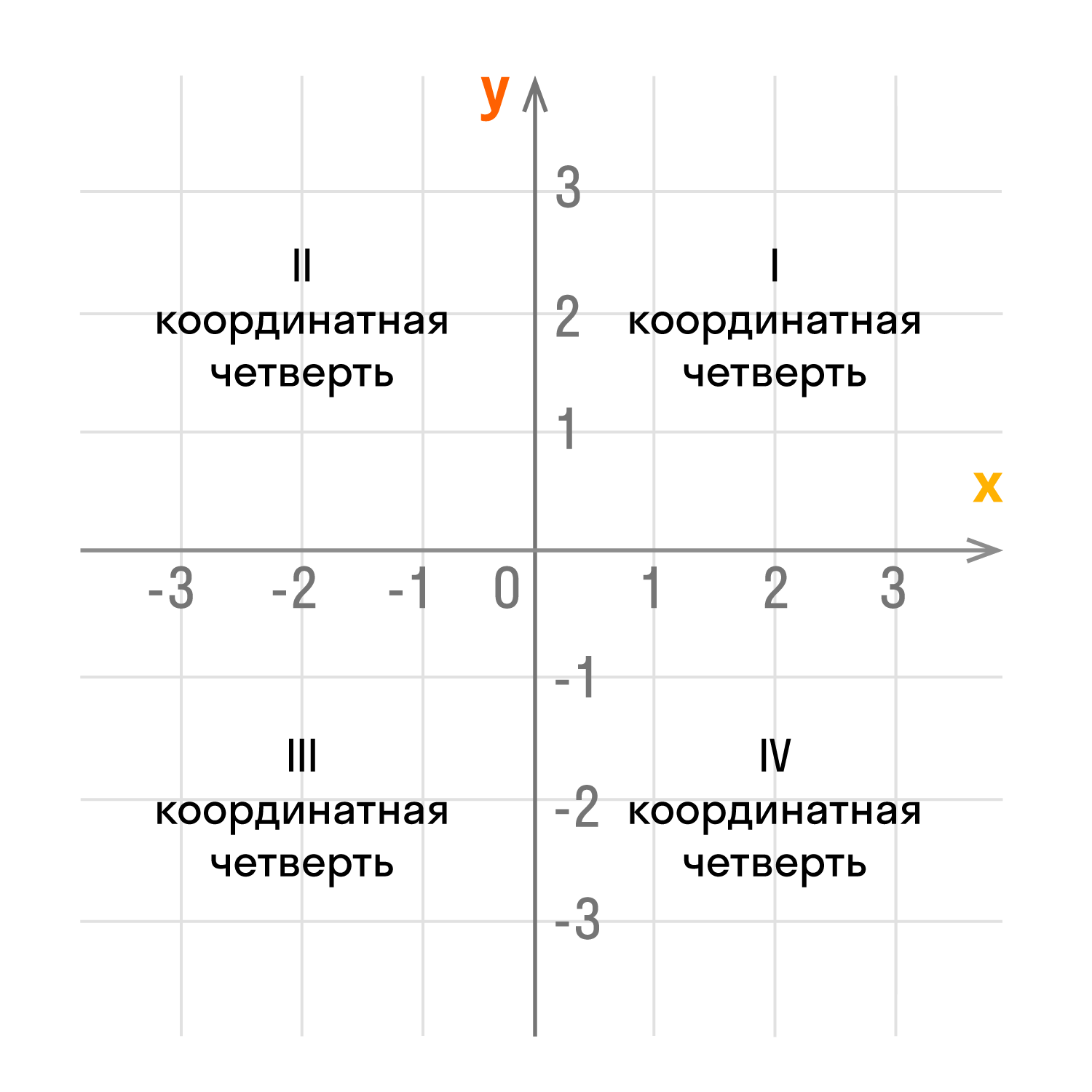
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Видео:Координатная плоскость | Ось абсцисс | Ось ординат | МегаШкола | Математика 6 классСкачать

Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
Видео:Система координат · Ось абсцисс и ось ординат · Координатная плоскость Урок Математики для 6 классаСкачать

Где абсцисса а где ордината на графике
Знание — сила. Познавательная информация
Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Ось абсцисс, ось ординат
Эта ассоциация позволяет легко запомнить, что x — это ось абсцисс, а y — ось ординат и никогда больше не путать оси координат.
Ассоциация очень простая. Итак, есть ось абсцисс и ось ординат — ось x и ось y. Абсцисса начинается на букву «а», ордината — на букву «о». Что у нас в русском алфавите? Сначала идет буква «а», затем — буква «о». В латинском алфавите сначала идет «x», затем — «y». Соответственно, абсцисса — это x, ордината — это y.
Русский алфавит: а, о
Латинский алфавит: x, y
Соответствие: а-x, о-y ( А бсцисса — X , O рдината — Y ).
Для тех, кто путает, где на координатной плоскости ось x, а где — ось y, есть следующая ассоциация .
В прямоугольной системе координат ось X’X называется «осью абсцисс» .
При построении графиков функций, ось абсцисс обычно используется как область определения функции.
Ординатой (от лат. ordinatus – расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см. рис. 1). Если точка C принадлежит положительной полуоси OY, то ордината имеет положительное значение. Если точка C принадлежит отрицательной полуоси Y’O, то ордината имеет отрицательное значение. Если точка A лежит на оси X’X, то её ордината равна нулю.
В прямоугольной системе координат ось Y’Y называется «осью ординат» .
При построении графиков функций, ось ординат обычно используется как область значений функции.
В прямоугольной системе координат ось X’X называется «осью абсцисс» .
При построении графиков функций, ось абсцисс обычно используется как область определения функции.
Ординатой (от лат. ordinatus – расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см. рис. 1). Если точка C принадлежит положительной полуоси OY, то ордината имеет положительное значение. Если точка C принадлежит отрицательной полуоси Y’O, то ордината имеет отрицательное значение. Если точка A лежит на оси X’X, то её ордината равна нулю.
В прямоугольной системе координат ось Y’Y называется «осью ординат» .
При построении графиков функций, ось ординат обычно используется как область значений функции.
В математике , то по оси абсциссы ( / æ б ы ɪ с . Ə / ; множественная абсцисса или абсцисса или абсцисса ) и ординаты соответственно первые и вторые координаты из точки в системе координат .
Абсциссой точки является подписанный мерой его проекции на первичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный, после того, как : положительная).
Ордината точки является подписанный мерой его проекции на вторичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный, после того, как : положительная).
Обычно это горизонтальные и вертикальные координаты точки в двумерной прямоугольной декартовой системе координат . Термины также могут относиться к горизонтальным и вертикальным осям , соответственно (обычно х -Axis и у -Axis) из двумерный графика. Упорядоченная пара состоит из двух слагаемых-оси абсцисс (горизонтальная, как правило , х ) и оси ординат (вертикальной, как правило , у ) -Какой определяют положение точки в двумерном пространстве прямоугольной.
( Икс ⏞ абсцисса , Y ⏞ ордината ) ^ >, overbrace ^ >)>
Видео:№1011. Ответьте на вопросы: а) Может ли абсцисса точки единичной полуокружности иметь значения 0,3Скачать
содержание
Видео:№939. Найдите расстояние от точки М (3; -2): а) до оси абсцисс; б) до оси ординат;Скачать
Этимология
Хотя слово «абсцисса» (лат; «Linea абсцисса», «линия отрезана») используется , по крайней мере , так как De Practica Geometrie , опубликованной в 1220 году Фибоначчи (Леонардо из Пизы), его использование в его современном понимании может быть связано венецианский математик Стефано дельи Анджели в своей работе Miscellaneum Hyperbolicum, и др Parabolicum 1659.
В 1892 работы Лекциях по теории über Geschichte дер Mathematik, Том 2, ( « Лекции по истории математики ») немецкий историк математики Мориц Кантор пишет
«Wir Кеннен Keine ältere Benutzung де Wortes Abssisse в lateinischen Originalschriften [чем дельи Анджели – х]. Vielleicht Kommt дас Сусло в Übersetzungen дер Apollonischen Kegelschnitte VOR, WO Buch I Satz 20 из ἀποτεμνομέναις фильеры Rede ист, wofür ES Kaum Ein entsprechenderes lateinisches Сусло ALS абсцисса Гебен möchte «. «Мы не знаем , не ранее использования слова абсциссы латинских оригиналов [чем дельи Анджели – х]. Может быть , это слово происходит от переводов Аполлона коника , где в книге I, Глава 20 там появляется ἀποτεμνομέναις, для которых вряд ли было бы в случае необходимости латинское слово , как по оси абсцисс. «
Видео:АбсциссаСкачать

В параметрических уравнениях
В нескольких устаревшей использовании варианты, абсцисса точки может также относиться к любому числу , которое описывает положение точки вдоль некоторого пути, например параметр в параметрическом уравнении . Используемый в этом случае, по оси абсцисс можно рассматривать как координатно-геометрию аналога к независимой переменной в математической модели или эксперимента (с любыми ординат , заполняющих роль , аналогичную зависимых переменных ).
Видео:Алгебра 7 класс. 28 сентября. Зная абсциссу найти ординатуСкачать

Смотрите также
Видео:Точки на числовой окружностиСкачать

Рекомендации
Эта статья основана на материале , взятом из Бесплатный он-лайн словарь вычислительной до 1 ноября 2008 года и зарегистрированная в соответствии с «релицензировании» с точки зрения GFDL , версии 1.3 или более поздней версии.
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Высшая математика. Шпаргалка
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
- 1. Основные понятия. Системы координат. Прямые линии и их взаимное расположение
- 2. Условие нахождения трех точек на одной прямой. Уравнение прямой. Взаимное расположение точек и прямой. Пучок прямых.
- 3. Полярные параметры прямой. Нормальное уравнение прямой. Преобразование координат
- 4. Порядок алгебраических линий. Окружность. Эллипс. Гипербола. Парабола
- 5. Аналитическая геометрия в пространстве. Плоскость
- 6. Прямая в пространстве
Приведённый ознакомительный фрагмент книги Высшая математика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.
1. Основные понятия. Системы координат. Прямые линии и их взаимное расположение
Координата точки — это величина, определяющая положение данной точки на плоскости, на прямой или кривой линии или в пространстве. Значение координаты зависит от выбора начальной точки, от выбора положительного направления и от выбора единицы масштаба.
Прямоугольная система координат состоит из двух взаимно перпендикулярных прямых — осей, точка их пересечения — начало координат О, ось ОХ — ось абсцисс, ось ОY — ось ординат. На осях выбираются масштаб и положительное направление.
Положение точки М определяется двумя координатами: абсциссой х и ординатой у. Записывается так: М(х, у). Оси координат образуют четыре координатных угла I, II, III, IV. Если точка находится в I координатном угле (квадранте), то и абсцисса, и ордината ее положительные, если — во II квадранте, то абсцисса отрицательна, а ордината положительна, если в — III квадранте, и абсцисса, и ордината отрицательны, если — в IV квадранте, положительна абсцисса, а ордината отрицательна. У точки, лежащей на оси ординат, абсцисса равна нулю, и наоборот, если точка лежит на оси абсцисс, то ее ордината равна нулю.
Косоугольной системой координат аналогична прямоугольной, только оси координат пересекаются под углом не равным прямому. Прямоугольная и косоугольная системы относятся к декартовой системе координат.
Полярная система координат состоит из полюса О и полярной оси ОХ, проведенной из полюса. Положение точки определяется полярным радиусом ρ (отрезок ОМ) и полярным углом φ. Для полярного угла берется его главное значение (от — π до π). Числа ρ, φ называются полярными координатами точки М.
Связь между координатами точки в прямоугольной и полярной системах координат: x = r cosφ, y = r sinφ или:
Общее уравнение прямой линии (система координат прямоугольная): Ах + Ву + С = 0 (А и В одновременно не равны нулю).
Если В не равно нулю, то уравнение прямой: у = ах + b (здесь а = — А / В, b = — С / В). Здесь а есть тангенс угла наклона прямой к положительному направлению оси абсцисс, b равно длине отрезка от начала координат до точки пересечения рассматриваемой прямой с осью ординат. Уравнение прямой, параллельной оси абсцисс: у = b, уравнение оси абсцисс: у = 0; уравнение прямой, параллельной оси ординат: х = с, уравнение оси ординат: х = 0.
📽️ Видео
№ 5.10- Алгебра 10-11 класс МордковичСкачать
Уравнение окружности с центром на оси абсцисс, ординат или в начале координат. Урок 3. Геометрия 8.Скачать

135 Сумма векторов. Абсцисса, ордината, аппликата. (240)Скачать

10 класс. Числовая окружность на координатной плоскости.Скачать
9 класс. Геометрия. Тригонометрические функции угла от 0° до 180°. Единичная окружность. Урок #1Скачать

Прямоугольная система координат. Абсцисса и ордината.Скачать

Как найти координаты точек на тригонометрической окружностиСкачать

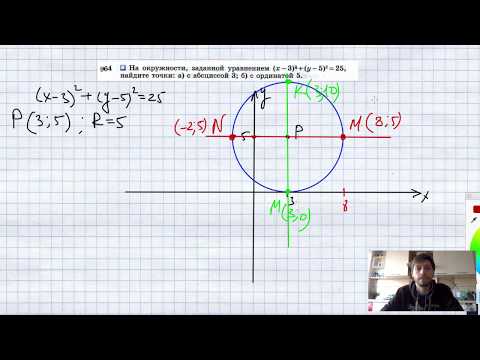
№964. На окружности, заданной уравнением (x-3)2 + + (y-5)2 = 25, найдите точки: а) с абсциссой 3;Скачать
Прямоугольная система координат. Координатная плоскость. 6 класс.Скачать

М10 (12.1-12.29) Тригонометрия. Задачи на координаты точки на числовой окружности.Скачать