Абсолютная погрешность радиуса окружности (3 видео)

Определение радиуса кривизны линзы R, входящей в устройство колец Ньютона, а также оценка доверительного интервала и относительной погрешности в определении величины R

Содержание

Страницы работы
Содержание работы
Погрешности измерений, представление результатов эксперимента
п.1. Шкала измерительного прибора
п.2. Цена деления
п.3. Виды измерений
п.4. Погрешность измерений, абсолютная и относительная погрешность
п.5. Абсолютная погрешность серии измерений
п.6. Представление результатов эксперимента
п.7. Задачи
Радиус круга равен 2см. Наидите погрешность допушенную при вычесления его площади,
📺 Видео

Страницы работы

Содержание работы

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

« ИНСТИТУТ ЦВЕТНЫХ МЕТАЛЛОВ И ЗОЛОТА»СФУ

Лабораторная работа № 6

Определение радиуса кривизны линзы

с помощью колец Ньютона

Красноярск 2010 г.

Цель работы: Определение радиуса кривизны линзы R, входящей в устройство колец Ньютона, а также оценка доверительного интервала и относительной погрешности в определении величины R.

Оборудование: Оптическая скамья, осветитель, диафрагма, прибор Ньютона, линза-объектив, экран, светофильтр.

Кольца Ньютона наблюдаются в случае соприкосновении выпуклой поверхности плоско-выпуклой линзы малой кривизны с плоско-параллельной поверхностью. Воздушная прослойка между плоскостью и линзой имеет переменную толщину, разность хода интерферирующих их лучей зависит от толщины этой прослойки. Чем больше толщина воздушной прослойки, тем больше число наблюдаемых колец.

Кольца Ньютона могут наблюдаться в отраженном и проходящем свете.

В отраженном свете оптическая разность хода для колец Ньютона определяют, учитывая λ/2,условием:

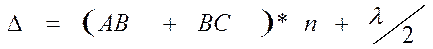
В отраженном свете по условию образовании максимума:

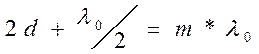
Для минимумов в отраженном свете:

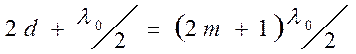
Так как на экране получаются увеличенные интерференционные кольца, то вначале надо рассчитать радиусы действительных колец:

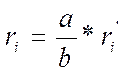
Радиусы действительных колец рассчитывают для опыта с проходящим и отраженным светом. В первом случае берут радиусы колец определенного цвета, во втором – радиусы темных колец при условии, что в опыте с отраженным светом использовали фильтр того же цвета.

Радиус кривизны линзы, входящей в устройство колец Ньютона, определяется теоретически по формуле:

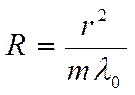
Так как практически трудно добиться идеального контакта сферической поверхности линзы и плоской пластинки в одной точке вследствие упругой деформации стекла и падения в место соприкосновения пылинки, то формулу использовать непосредственно нельзя: кольцу с номером m в действительности может соответствовать номер (m+p), где p – неизвестное целое число, одинаковое для всех колец. Для исключения числа p вычисление радиуса кривизны надо делать по разности квадратов радиуса двух колец:

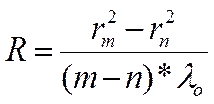
Измеряем радиусы полученных колец:

; ; .

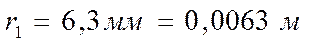
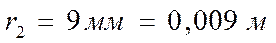
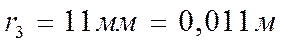
Вычисляем радиусы действительных колец по формуле:

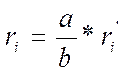
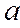
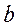
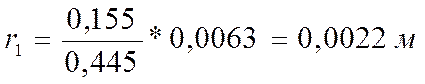
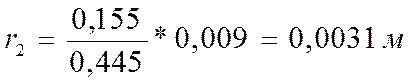
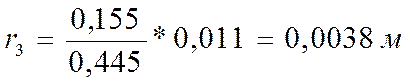
где =155 мм=0,155 м; =445мм=0,445м.

;

После того как мы вычислили действительные радиусы колец, вычисляем радиус кривизны линзы по формуле:

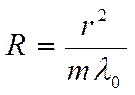
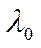
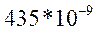
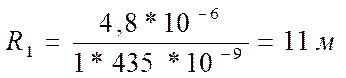
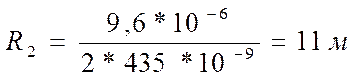
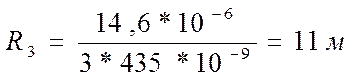
Где =435 Нм=м,

;

Найдем среднее значение:

;

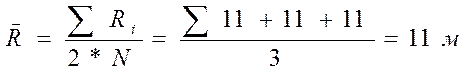
Найдем средне квадратичную погрешность:

;

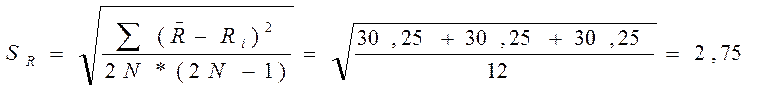
Доверительный интервал найдем по формуле:

; ;

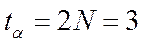
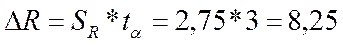
Найдем относительную погрешность:

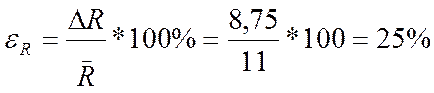
Вывод: Мы определили радиусы кривизны линзы R, входящей в устройство колец Ньютона, а также оценили доверительный интервал и относительную погрешность в определении величины R.

Видео:Относительная и абсолютная погрешностьСкачать

Погрешности измерений, представление результатов эксперимента

п.1. Шкала измерительного прибора

Примеры шкал различных приборов:

Абсолютная погрешность радиуса окружности

Манометр – прибор для измерения давления, круговая шкала

Вольтметр – прибор для измерения напряжения, дуговая шкала

Индикатор громкости звука, линейная шкала

п.2. Цена деления

Пример определения цены деления:

Определим цену деления основной шкалы секундомера.
Два ближайших пронумерованных деления на основной шкале: a = 5 c
b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.

Цена деления: begin triangle=frac\ triangle=frac=frac15=0,2 c end

п.3. Виды измерений

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Определяется субъективным фактором, ошибками экспериментатора.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

определение длины с помощью линейки или мерной ленты;
определение объема с помощью мензурки.

Пример получения результатов прямых измерений с помощью линейки:

Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями.
Цена деления такой линейки: begin triangle=frac= frac<1 text>=0,5 text end Инструментальная погрешность: begin d=frac=frac=0,25 text end Истинное значение: (L_0=4 text)
Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text $$ Относительная погрешность: $$ delta=fraccdot 100text=6,25textapprox 6,3text $$

Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями.
Цена деления такой линейки: begin triangle=frac= frac<1 text>=0,1 text end Инструментальная погрешность: begin d=frac=frac=0,05 text end Истинное значение: (L_0=4,15 text)
Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text $$ Относительная погрешность: $$ delta=fraccdot 100textapprox 1,2text $$

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

№ опыта	1	2	3	Сумма
Масса, г	99,8	101,2	100,3	301,3
Абсолютное отклонение, г	0,6	0,8	0,1	1,5

Сначала находим среднее значение всех измерений: begin m_0=frac=fracapprox 100,4 text end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end Находим среднее абсолютное отклонение: begin triangle_=frac=frac=0,5 text end Мы видим, что полученное значение (triangle_) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin triangle m=maxleft<triangle_; dright>=maxleft text end Записываем результат: begin m=m_0pmtriangle m\ m=(100,4pm 0,5) text end Относительная погрешность (с двумя значащими цифрами): begin delta_m=fraccdot 100textapprox 0,050text end

п.6. Представление результатов эксперимента

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

№ мензурки	a, мл	b, мл	n	(triangle=frac), мл
1	20	40	4	(frac=4)
2	100	200	4	(frac=20)
3	15	30	4	(frac=3)
4	200	400	4	(frac=40)

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

№ мензурки	Объем (V_0), мл	Абсолютная погрешность (triangle V=frac), мл	Относительная погрешность (delta_V=fraccdot 100text)
1	68	2	3,0%
2	280	10	3,6%
3	27	1,5	5,6%
4	480	20	4,2%

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text, x_2=(4,0pm 0,03) text $$ Какое из этих измерений точней и почему?

Мерой точности является относительная погрешность измерений. Получаем: begin delta_1=fraccdot 100text=2,5text\ delta_2=fraccdot 100text=0,75text end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac=5 (text), triangle v_2=frac=0,5 (text) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text, v_2=(72pm 0,5) text $$ Скорость сближения равна сумме скоростей: $$ v_0=v_+v_, v_0=54+72=125 text $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text $$ Относительная погрешность: $$ delta_v=fraccdot 100textapprox 4,4text $$ Ответ: (v=(126,0pm 5,5) text, delta_vapprox 4,4text)

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Инструментальная погрешность линейки (d=frac=0,05 text)
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text, b=(60,10pm 0,05) text $$ Относительные погрешности (не забываем про правила округления): begin delta_1=fraccdot 100textapprox 0,0554textapprox uparrow 0,056text\ delta_2=fraccdot 100textapprox 0,0832textapprox uparrow 0,084text end Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text+0,084text=0,140text=0,14text $$ Абсолютная погрешность: begin triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text^2\ S=(5421,0pm 7,6) text^2 end Ответ: (S=(5421,0pm 7,6) text^2, delta_Sapprox 0,14text)

Видео:Расчет абсолютной погрешностиСкачать

Радиус круга равен 2см. Наидите погрешность допушенную при вычесления его площади,

Радиус круга равен 2см. Наидите погрешность допушенную при вычесления его площади, если погрешность при измерении длины радиуса одинакова: 1) 0,2см. 2) 0,1 ; 3)h

Regina Marzjuk
Алгебра 2018-12-14 22:34:38 18 2