45 градусов на треугольнике (3 видео) | Курс школьной геометрии

Прямоугольные треугольники

Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).

Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Содержание

Некоторые свойства прямоугольного треугольника:
Соотношение между сторонами и углами в прямоугольном треугольнике:
Значения тригонометрических функций некоторых углов:
Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45)
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ПРИ α=45°
Табличные значения: синус 45, косинус 45 и тангенс 45 градусов
Синус, косинус и тангенс угла π/4 радиан
Значение тригонометрических функций углов 30°, 45° и 60°
30° и 60°
💡 Видео

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

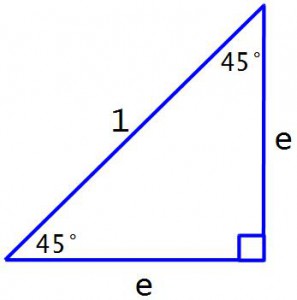
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.

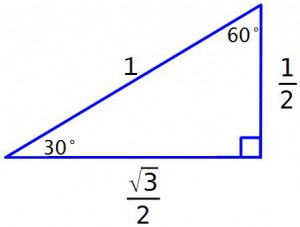
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.

5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$

6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$

7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.

6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.

7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$/$	$/$	$/$
$cosα$	$/$	$/$	$/$
$tgα$	$/$	$1$	$√3$
$ctgα$	$√3$	$1$	$/$

Площадь прямоугольного треугольника равна половине произведения его катетов

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√$. Найдите косинус внешнего угла при вершине $В$.

Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то

Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:

Катет $ВС$ мы можем найти по теореме Пифагора:

Подставим найденное значение в формулу косинуса

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sin⁡A=/, AC=9$. Найдите $АВ$.

Распишем синус угла $А$ по определению:

Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.

Применим теорему Пифагора, чтобы отыскать $«х»$

Так как длина $АВ$ составляет пять частей, то $3∙5=15$

В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:

Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.

В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.

Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.

Видео:Построение углов заданной градусной мерыСкачать

Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45)

Табличные значения синуса 45, косинуса 45 и тангенса 45 градусов указаны ниже. Далее по тексту следует пояснение метода и правильности вычисления этих значений для произвольного прямоугольного треугольника.

45 градусов — это π/4 радиан. Формулы для значений косинуса, синуса и тангенса пи/4 радиан указаны ниже (хотя они и тождественны).
То есть, например, tg π/4 = tg 45 градусов

Видео:Треугольники с углами 45, 45 и 90 градусовСкачать

ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ПРИ α=45°

Как самостоятельно вычислить значения sin cos tg 45 градусов?

Построим и рассмотрим прямоугольный треугольник АВС у которого угол ∠В = 45°. На основании соотношения его сторон, вычислим значения тригонометрических функций в прямоугольном треугольнике для угла 45 градусов. Поскольку треугольник прямоугольный, то значения функций синуса, косинуса и тангенса будут равны соотношению его соответствующих сторон.

Поскольку значение функций синуса, косинуса и тангенса зависят исключительно от градусной меры угла (или значения, выраженного в радианах), то найденные нами соотношения и будут значениями функции синуса 45, косинуса 45 и тангенса 45 градусов.

Согласно свойствам прямоугольного треугольника, угол С — прямой и равен 90 градусам. Угол B мы изначально построили с градусной мерой 45 градусов. Найдем значение угла А. Так как сумма углов треугольника равна 180 градусам, то

∠А + ∠В + ∠С = 180°
Угол C прямой и равен 90 градусам, угол B мы изначально определили как 45 градусов, таким образом:
∠А = 180° —∠С — ∠В = 180° — 90° — 45° = 45°

Поскольку у данного треугольника два угла равны между собой, то треугольник АВС – прямоугольный, и, одновременно, равнобедренный, в котором оба катета равны между собой: AC = BC.

Допустим, что длина сторон равна некому числу АС = ВС = а. Зная длины катетов, вычислим длину гипотенузы.

По теореме Пифагора: АВ 2 =АС 2 +ВС 2
Заменим длины AC и BC на переменную а, тогда получим:

АВ 2 = а 2 + а 2 = 2а 2 ,

В результате мы выразили длины всех сторон прямоугольного треугольника с углом 45 градусов через переменную а.

Согласно свойств тригонометрических функций в прямоугольном треугольнике соотношение соответствующих сторон треугольника будет равным значению соответствующих функций. Таким образом для угла α = 45 градусов:

sin α = BC / AB (согласно определению синуса для прямоугольного треугольника — это отношение противолежащего катета к гипотенузе, BC — катет, AB — гипотенуза)

cos α = AC / AB (согласно определению косинуса — это отношение прилежащего катета к гипотенузе, AC — катет, AB — гипотенуза)

tg α = BC / AC (аналогично, тангенс для угла α будет равен отношению противолежащего катета к прилежащему)

Вместо обозначений сторон подставим значения их длин через переменную а.

Исходя из этого (см. таблицу значений sin 45, cos 45, tg 45) получаем:

Табличные значения sin 45, cos 45, tg 45 (то есть значение синуса 45, косинуса 45 и тангенса 45 градусов можно вычислить как соотношение соответствующих сторон данного треугольника), подставим вычисленные выше значения длин сторон в формулы и получим результат на картинке ниже.

Видео:Геометрия ОГЭ задача Теорема синусовСкачать

Табличные значения: синус 45, косинус 45 и тангенс 45 градусов

Таким образом:

тангенс 45 градусов равен единице
синус 45 градусов равен косинусу 45 градусов и равен корню из двух пополам (то же самое, что и единица, деленная на корень из двух)

Видео:Задача 6 №27591 ЕГЭ по математике. Урок 59Скачать

Синус, косинус и тангенс угла π/4 радиан

тангенс π/4 ( пи на четыре) равен единице
синус π/4 ( пи на четыре) градусов равен косинусу π/4 градусов и равен корню из двух пополам

Примечание. В поисковых запросах часто встречается нечто типа «тангенс р/4 или p/4». Это неграмотно. Используйте запрос, например «тангенс пи/4».

Видео:Классный способ для разметки любого угла без транспортира.Скачать

Значение тригонометрических функций углов 30°, 45° и 60°

Найдем значение Sin, Cos, Tg, Ctg трёх примечательных углов 30°, 45° и 60°.

30° и 60°

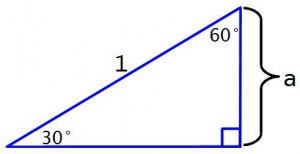
Начнём с синуса 30°. Для этого построим прямоугольный треугольник с острым углом в 30°. И синус 30° – это будет отношение противолежащего короткого катета к гипотенузе. И для удобства установим длину гипотенузы единица.

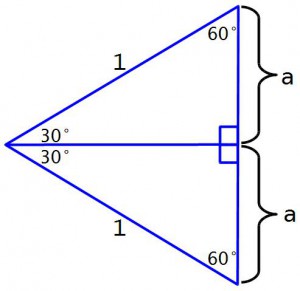
И тогда получается что отношение длины катета к гипотенузе равно просто длине катета, и синус 30° будет равен просто а. Кроме того, сумма углов любого треугольника равна 180°, и 2й острый угол равен 180° – 90° – 30° = 60°. И для 2го острого угла отношение короткого катета к гипотенузе – это будет отношение прилежащего катета к гипотенузе то есть косинус. И значит, Cos(60°) тоже будет равен а. А теперь найдем, чему же равно это а. Для этого построим снизу ещё один такой же треугольник, равный исходному — только отраженный зеркально.

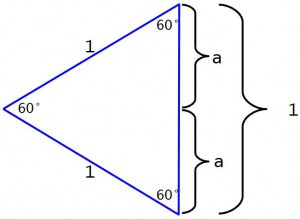
И вот что получается: во-первых приглядимся к углу, сложившемуся из двух прямых углов – он развернутый. Получается, что верхняя и нижняя точки треугольника и вершина прямых углов лежат на одном отрезке. А левый угол складывается из двух углов по 30°, то есть равен он 60°. Следовательно, можно стереть горизонтальный отрезок, и получается треугольник, у которого каждый угол равен 60°.

Равносторонний треугольник, у которого третья сторона равна первым двум сторонам и тоже равна единице. Получилось, что:

А это означает, что

И таким образом

Sin(30°) = Cos(60°) = 1/2

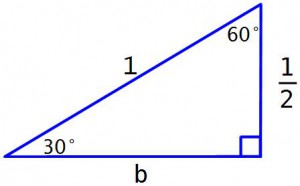
Теперь вернемся к исходному треугольнику. Короткий катет теперь известен – это 1/2. А чему же равен длинный катет? Обозначим его буквой b.

Для угла в 30° этот катет b – прилежащий, гипотенуза равна 1. И значит длина этого катета равна отношению длины прилежащего катета к гипотенузе, то есть Cos(30°). А для 60° этот длинный катет – противолежащий. И следовательно длина этого катета равна отношению противолежащего катета к гипотенузе, то есть Sin(60°). И значит

Cos(30°) = Sin(60°) = b

Ну а теперь найдем катет b с помощью теоремы Пифагора. Как известно, сумма квадратов катетов равна квадрату гипотенузы, то есть

Cos(30°) = Sin(60°) = (√3)/2

Теперь уже известны оба катета, и можно найти отношение двух катетов. Сначала найдём отношение короткого катета к длинному катету. Для угла в 30° это будет отношение противолежащего катета к прилежащему катету, то есть Tg(30°). А для угла в 60° это будет наоборот – отношение прилежащего катета к противолежащему катету то есть Ctg(60°).

А теперь наоборот длинный катет разделим на короткий катет. Для 30° это будет прилежащий катет разделить на противолежащий, то есть Ctg(30°). А для 60° это будет противолежащий катет разделить на прилежащий, то есть Tg(60°).

Построим прямоугольный треугольник с острым углом 45 градусов. Гипотенузу опять сделаем единицу и противолежащий катет обозначим буквой e.

Отношение противолежащего катета к гипотенузе и будет равно Sin(45°). Но гипотенуза – единица – поэтому просто длина этого катета равна синусу Sin(45°). Теперь обратим внимание на 2й острый угол. На два острых угла в прямоугольном треугольнике приходится 90°. Значит 2й острый угол равен 90° – 45° = 45°. Выходит что этот прямоугольный треугольник – равнобедренный, и второй катет тоже равен е. И получается что для угла 45° отношение прилежащего катета к гипотенузе такое же, как и противолежащего катета к гипотенузе

Cos(45°) = Sin(45°) = е

Кроме того, даже не зная, чему равно е, можно сказать, какой будет Tg(45°) и Ctg(45°), потому что отношение противолежащего катета к прилежащему или, наоборот, прилежащего катета к противолежащему – будет равно единице.

Tg(45°) = Ctg(45°) = e / e = 1

Ну а теперь можно уже наконец найти, чему равно е. И для этого воспользуемся теоремой Пифагора.

Cos(45°) = Sin(45°) = (√2)/2

И таким образом найдены значения основных тригонометрических функций углов 30° 45° и 60°.