311387 в треугольнике угол

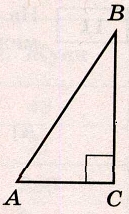
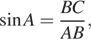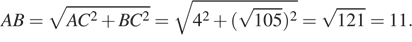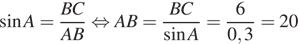Прямоугольный треугольник

Задание 16 № 118

В тре­уголь­ни­ке ABC угол C прямой, BC = 8 , sin A = 0,4. Найдите AB.

Решение.

Синус угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го ка­те­та ВС к ги­по­те­ну­зе АВ. Поэтому:

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1309.

Задание 16 № 132773

Два ост­рых угла пря­мо­уголь­но­го тре­уголь­ни­ка от­но­сят­ся как 4:5. Най­ди­те боль­ший ост­рый угол. Ответ дайте в градусах.

Решение.

Сумма ост­рых углов пря­мо­уголь­но­го тре­уголь­ни­ка равна 90°. Ост­рые углы пря­мо­уголь­но­го тре­уголь­ни­ка от­но­сят­ся как 4 части к 5 частям, сумма этих углов 4 + 5 = 9 частей. По­это­му одна часть равна 10°. Так как боль­ший угол со­дер­жит в себе 5 частей, он равен 5·10° = 50°.

Задание 16 № 311387

В тре­уголь­ни­ке угол равен 90°, . Най­ди­те .

Решение.

Так как тре­уголь­ник ABC — прямоугольный, то . Имеем:

Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)

Задание 16 № 311399

В тре­уголь­ни­ке угол равен 90°, . Найдите .

Решение.

Так как тре­уголь­ник ABC — прямоугольный, то . Имеем:

Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)

Задание 16 № 311498

В тре­уголь­ни­ке угол прямой, . Най­ди­те .

Решение.

Треугольник ABC — прямоугольный. Таким образом,

Источник: ГИА-2013. Математика. Экзамен. Вариант 9

Задание 16 № 311500

В тре­уголь­ни­ке угол прямой, . Най­ди­те .

Решение.

Треугольник ABC — прямоугольный. Таким образом,

Источник: ГИА-2013. Математика. Экзамен. Вариант 10

Задание 16 № 311760

В тре­уголь­ни­ке ABC угол C равен 90°, AC = 20, tgA = 0,5. Най­ди­те BC.

Решение.

Тангенс угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го ка­те­та к прилежащему, поэтому

Задание 16 № 311816

В тре­уголь­ни­ке ABC угол C равен 90°, BC = 20, = 0,5. Най­ди­те AC.

Решение.

Тан­генс угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го углу ка­те­та к при­ле­жа­ще­му:

Задание 16 № 316283

В тре­уголь­ни­ке ABC угол C равен 90°, BC = 12 , tgA = 1,5. Най­ди­те AC.

Решение.

Тан­генс угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го углу ка­те­та к при­ле­жа­ще­му:

Задание 16 № 316320

В тре­уголь­ни­ке ABC угол C равен 90°, AC = 12 , tgA = 1,5. Най­ди­те BC.

Решение.

Тан­генс угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го углу ка­те­та к при­ле­жа­ще­му поэтому:

Задание 16 № 322819

Ка­те­ты пря­мо­уголь­но­го тре­уголь­ни­ка равны 35 и 120. Най­ди­те вы­со­ту, про­ве­ден­ную к ги­по­те­ну­зе.

Решение.

Пусть ка­те­ты имеют длины и а ги­по­те­ну­за — длину Пусть длина высоты, проведённой к ги­по­те­ну­зе равна Найдём длину ги­по­те­ну­зы по тео­ре­ме Пифагора:

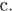
Площадь пря­мо­уголь­но­го тре­уголь­ни­ка может быть най­де­на как по­ло­ви­на про­из­ве­де­ния ка­те­тов или как по­ло­ви­на про­из­ве­де­ния высоты, проведённой к ги­по­те­ну­зе на гипотенузу:

Задание 16 № 322979

Ка­те­ты пря­мо­уголь­но­го тре­уголь­ни­ка равны и 1. Най­ди­те синус наи­мень­ше­го угла этого тре­уголь­ни­ка.

Решение.

Пусть ка­те­ты имеют длины и а ги­по­те­ну­за — длину Найдём длину ги­по­те­ну­зы по тео­ре­ме Пифагора:

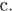
Наименьший угол в тре­уголь­ни­ке лежит про­тив наи­мень­шей стороны, 4 > 1 следовательно, синус наи­мень­ше­го угла равен:

Задание 16 № 323344

Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна Один из ост­рых углов равен 30°. Най­ди­те длину ги­по­те­ну­зы.

Решение.

Пусть — длина катета, лежащего против угла в 30°, тогда гипотенуза равна второй катет равен .

Площадь прямоугольного треугольника равна половине произведения катетов.

Следовательно, длина гипотенузы, равна 16.

Приведём другое решение.

Пусть длина ги­по­те­ну­зы равна а длина катета, при­ле­жа­ще­го к углу 30° равна Пло­щадь тре­уголь­ни­ка можно найти как по­ло­ви­ну про­из­ве­де­ния двух сто­рон на синус угла между ними:

Задание 16 № 339365

В тре­уголь­ни­ке угол равен 90°, Най­ди­те

Решение.

По опре­де­ле­нию тан­ген­са от­ку­да По тео­ре­ме Пифагора:

Задание 16 № 339370

В тре­уголь­ни­ке угол равен 90°, Най­ди­те

Решение.

Найдём ко­си­нус угла

По опре­де­ле­нию косинуса, от­ку­да

Задание 16 № 339385

Площадь пря­мо­уголь­но­го тре­уголь­ни­ка равна Один из ост­рых углов равен 30°. Най­ди­те длину катета, ле­жа­ще­го на­про­тив этого угла.

Решение.

Пусть длина ги­по­те­ну­зы равна а длина катета, ле­жа­ще­го на­про­тив угла 30° равна Сумма углов в тре­уголь­ни­ке равна 180°, следовательно, вто­рой ост­рый угол равен 180° − 90° − 30° = 60°. Пло­щадь тре­уголь­ни­ка можно найти как по­ло­ви­ну про­из­ве­де­ния двух сто­рон на синус угла между ними:

Задание 16 № 339406

Площадь пря­мо­уголь­но­го тре­уголь­ни­ка равна Один из ост­рых углов равен 30°. Най­ди­те длину катета, при­ле­жа­ще­го к этому углу.

Решение.

Пусть длина ги­по­те­ну­зы равна а длина катета, при­ле­жа­ще­го к углу 30° равна Пло­щадь тре­уголь­ни­ка можно найти как по­ло­ви­ну про­из­ве­де­ния двух сто­рон на синус угла между ними:

Задание 16 № 339436

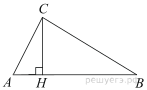
Точка H яв­ля­ет­ся ос­но­ва­ни­ем высоты, проведённой из вер­ши­ны пря­мо­го угла B тре­уголь­ни­ка ABC к ги­по­те­ну­зе AC. Най­ди­те AB, если AH = 6, AC = 24.

Решение.

Рассмотрим тре­уголь­ни­ки и они — прямоугольные, угол — общий, следовательно, тре­уголь­ни­ки подобны. Откуда:

Источник: Банк заданий ФИПИ

Задание 16 № 340000

В пря­мо­уголь­ном тре­уголь­ни­ке катет , а вы­со­та , опу­щен­ная на гипотенузу, равна Най­ди­те

Решение.

Из пря­мо­уголь­но­го тре­уголь­ни­ка по тео­ре­ме Пи­фа­го­ра найдём

Углы и равны как углы с вза­им­но пер­пен­ди­ку­ляр­ны­ми сторонами, по­это­му их си­ну­сы равны:

Задание 16 № 340078

В тре­уголь­ни­ке ABC угол C равен 90°, AC = 4, tg A = 0,75. Най­ди­те BC.

Решение.

По опре­де­ле­нию тангенса:

Задание 16 № 340384

В тре­уголь­ни­ке = 35, угол равен 90°. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этого треугольника.

Решение.

По тео­рем Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 341380

Найдите пло­щадь пря­мо­уголь­но­го треугольника, если его катет и ги­по­те­ну­за равны со­от­вет­ствен­но 12 и 13.

Решение.

По тео­ре­ме Пифагора най­дем второй катет: , зна­чит, площадь равна:

Задание 16 № 348415

Катеты прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого треугольника.

Решение.

По теореме Пифагора сумма квадратов катетов ( ) равна квадрату гипотенузы ( ). Таким образом:

Задание 16 № 348419

В прямоугольном треугольнике катет и гипотенуза равны 40 и 41 соответственно. Найдите другой катет этого треугольника.

Решение.

По теореме Пифагора сумма квадратов катетов ( ) равна квадрату гипотенузы ( ). Таким образом:

Задание 16 № 348430

В прямоугольном треугольнике катет и гипотенуза равны 40 и 50 соответственно. Найдите другой катет этого треугольника.

Решение.

По теореме Пифагора сумма квадратов катетов ( ) равна квадрату гипотенузы ( ). Таким образом:

Задание 16 № 348615

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 348758

Один из острых углов прямоугольного треугольника равен 23°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен

Задание 16 № 348837

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­рем Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 348945

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­рем Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 348999

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­рем Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 349009

В треугольнике угол равен 90°, , . Найдите .

Решение.

Синус угла равен от­но­ше­нию про­ти­во­ле­жа­ще­го ка­те­та ВС к ги­по­те­ну­зе АВ. Поэтому:

Задание 16 № 349061

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 349073

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 349084

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 349181

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла — отношение противолежащего катета к гипотенузе, следовательно:

Задание 16 № 349193

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла — отношение противолежащего катета к гипотенузе, следовательно:

Задание 16 № 349195

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла — отношение противолежащего катета к гипотенузе, следовательно:

Задание 16 № 349225

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 349294

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла — отношение противолежащего катета к гипотенузе, следовательно:

Задание 16 № 349357

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла — отношение противолежащего катета к гипотенузе, следовательно:

Задание 16 № 349434

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 349483

Один из острых углов прямоугольного треугольника равен 21°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен

Задание 16 № 349485

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 349522

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 349526

Один из острых углов прямоугольного треугольника равен 43°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен

Задание 16 № 349534

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 349585

В треугольнике угол равен 90°, , . Найдите .

Решение.

В прямоугольном треугольнике синус угла — отношение противолежащего катета к гипотенузе, следовательно:

Задание 16 № 349686

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 349694

Один из острых углов прямоугольного треугольника равен 63°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен

Задание 16 № 349799

В прямоугольном треугольнике катет и гипотенуза равны 5 и 13 соответственно. Найдите другой катет этого треугольника.

Решение.

По теореме Пифагора в прямоугольном треугольнике сумма квадратов катетов ( ) равна квадрату гипотенузы . Таким образом,

Задание 16 № 349840

В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

Решение.

По тео­реме Пи­фа­го­ра найдём сто­ро­ну

Радиус окружности, описанной вокруг прямоугольного треугольника равен половине гипотенузы.

Задание 16 № 349868

Два катета прямоугольного треугольника равны 16 и 30. Найдите гипотенузу этого треугольника.

Решение.

По теореме Пифагора в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы . Таким образом,

Задание 16 № 349873

Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.

Решение.

Сумма углов в треугольнике равна 180°. Таким образом, искомый угол равен

Задание 16 № 350007

В треугольнике угол равен 90°, , . Найдите .

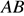
Решение.

В прямоугольном треугольнике синус угла — отношение противолежащего катета к гипотенузе, следовательно:

Задание 16 № 353514

Точка H яв­ля­ет­ся ос­но­ва­ни­ем высоты, проведённой из вер­ши­ны пря­мо­го угла B тре­уголь­ни­ка ABC к ги­по­те­ну­зе AC. Най­ди­те AB, если AH = 8, AC = 32.

Видео:В треугольнике отмечены середины M и N сторон BC и AC ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

В треугольнике ABC угол C равен 90°, tg B = 8/15, BC = 30. Найдите площадь треугольника

Видео:Задача 6 №27922 ЕГЭ по математике. Урок 139Скачать

Ваш ответ

Видео:В треугольнике угол С равен 90 градусов, M - середина стороны AB, AB = 20, BC = 10. Найдите CM.Скачать

решение вопроса

Видео:Задача 6 №27357 ЕГЭ по математике. Урок 46Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,049
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:ЕГЭ Математика Задание 6#27778Скачать

Решение №2240 В треугольнике АВС угол С равен 90°, ВС = 15, АС = 3. Найдите tgВ.

В треугольнике АВС угол С равен 90°, ВС = 15, АС = 3. Найдите tgВ.

Источник: ОГЭ Ященко 2022 (36 вар)

Тангенс острого угла прямоугольного треугольника – это отношение противолежащего катета к прилежащему катету.

Ответ: 0,2.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 4

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

📹 Видео

ПОЧЕМУ СУММА УГЛОВ В ТРЕУГОЛЬНИКЕ РАВНА 180? #shorts #геометрия #егэ #огэ #треугольникСкачать

Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

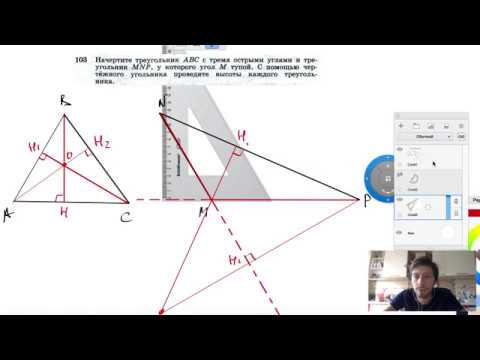
№103. Начертите треугольник ABC с тремя острыми углами и треугольник MNP, у которого угол М тупой.Скачать

ЗАДАНИЕ 6 из ЕГЭ_6Скачать

Задание 24 ОГЭ по математике #7Скачать

Задача 6 №27886 ЕГЭ по математике. Урок 123Скачать

В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найти меньший угол треугольника ABCСкачать

Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

ОГЭ 2020 задание 16Скачать

Геометрия ОГЭ задача Теорема синусовСкачать

ОГЭ/База Все прототипы задач с треугольникамиСкачать

ОГЭ по математике. В треугольнике АБС известно три стороны. Найди косинус угла. (Вар.8) √ 16Скачать

Задание 3 ЕГЭ по математике. Урок 41Скачать

Как правильно решить задание про четырёхугольник? / Разбор заданий на ОГЭ по геометрииСкачать