2 черточки на треугольнике

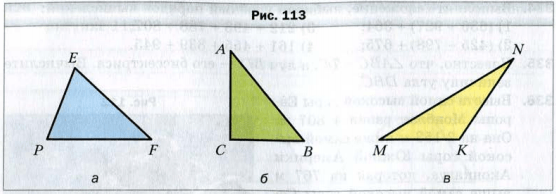
Из всех многоугольников треугольники имеют наименьшее количество углов и сторон.

Треугольники можно различать по виду их углов.

Есди все углы треугольника острые, то его называют остроугольным треугольником (рис. 113, а).

Если один из углов треугольника прямой, то его называют прямоугольным треугольником (рис. 113, б).

Если один из углов треугольника тупой, то его называют тупоугольным треугольником (рис. 113, в).

Говорят, что мы классифицировали треугольники по виду их углов.

Треугольники можно классифицировать не только по виду углов, но и по количеству равных сторон.

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

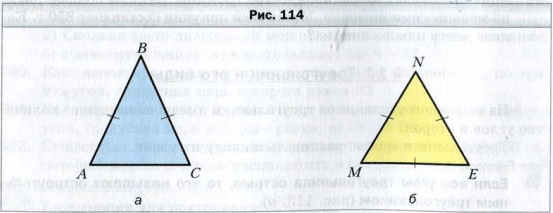
На рисунке 114, а изображен равнобедренный треугольник ABC, у которого AB = BC. На рисунке равные стороны отмечают равным количеством черточек. Равные стороны AB и BC называют боковыми сторонами, а сторону AC − основанием равнобедренного треугольника ABC.

Если стороны треугольника равны, то его называют равносторонним треугольником.

Треугольник, изображенный на рисунке 114, б, − равносторонний, у него MN = NE = EM.

Треугольник, у которого три стороны имеют различную длину, называют разносторонним треугольником.

Треугольники, изображенные на рисунке 113, − разносторонние. Если сторона равностороннего треугольника равна a, то его периметр вычисляют по формуле:

P = 3 a

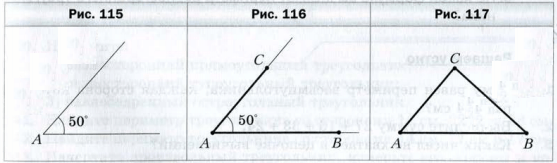
Пример 1 . С помощью линейки и транспортира постройте треугольник, две стороны которого равны 3 см и 2 см, а угол между ними − 50 °.

С помощью транспортира построим угол A, градусная мера которого 50 ° (рис. 115 ). На сторонах этого угла от его вершины с помощью линейки отложим отрезок AB длиной 3 см и отрезок AC длиной 2 см (рис. 116 ). Соединив отрезком точки B и C, получим искомый треугольник ABC ( рис. 117 ).

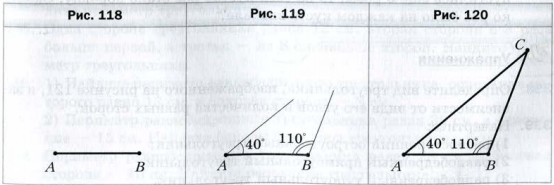
Пример 2 . С помощью линейки и транспортира постройте треугольник ABC, сторона AB которого равна 2 см, а углы CAB и CBA соответственно равны 40 ° и 110 °.

Решение. С помощью линейки строим отрезок AB длиной 2 см (рис. 118 ). От луча AB с помощью транспортира откладываем угол с вершиной в точке A, градусная мера которого равна 40 °. От луча BA в ту же сторону от прямой AB, в которую был отложен первый угол, откладываем угол с вершиной в точке B, градусная мера которого равна 110 °(рис. 119 ).

Найдя точку C пересечения сторон углов A и B, получаем искомый треугольник ABC ( рис. 120 ).

Видео:Эксперт (Короткометражка, Русский дубляж)Скачать

Признаки равенства треугольников

О чем эта статья:

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

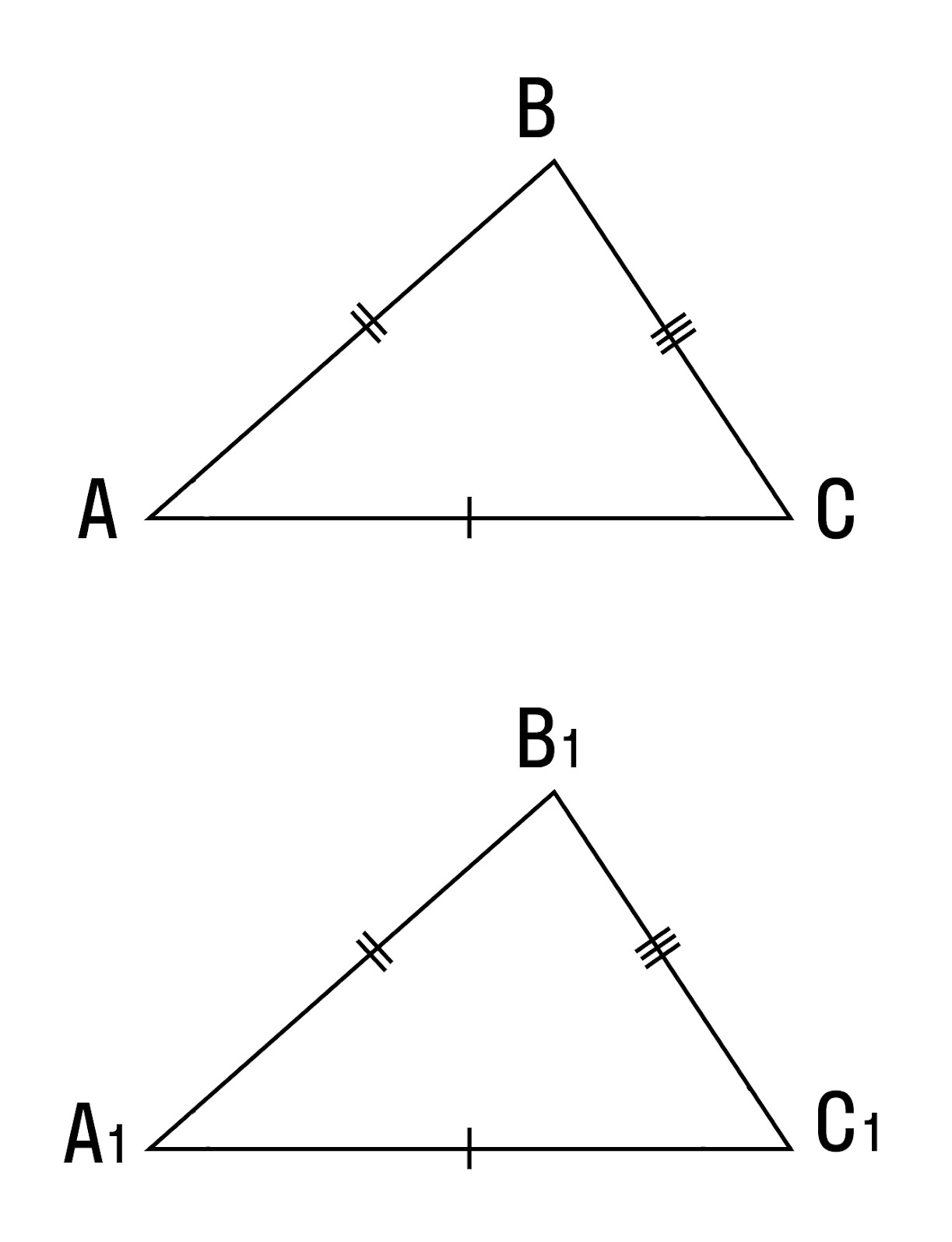
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Видео:Треугольники. 7 класс.Скачать

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Видео:Задача про полоски в треугольнике, которая ставит в тупик детейСкачать

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

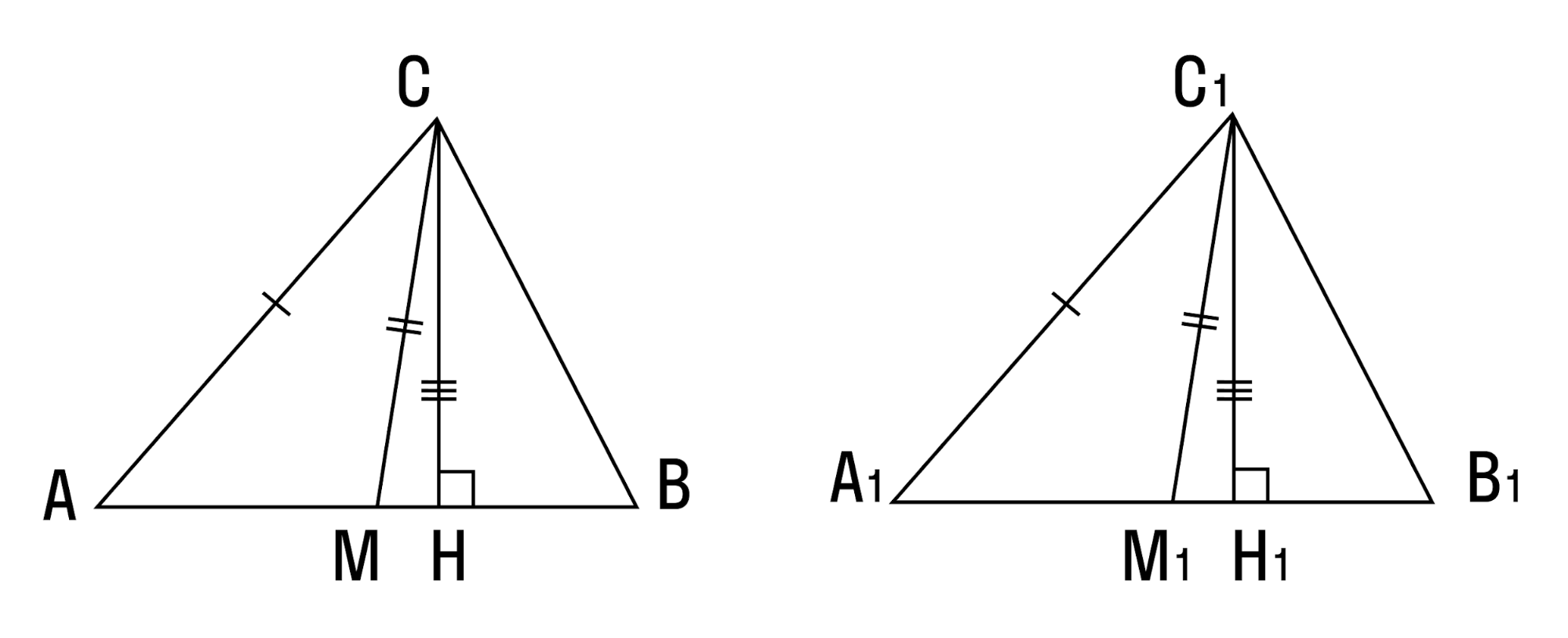
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

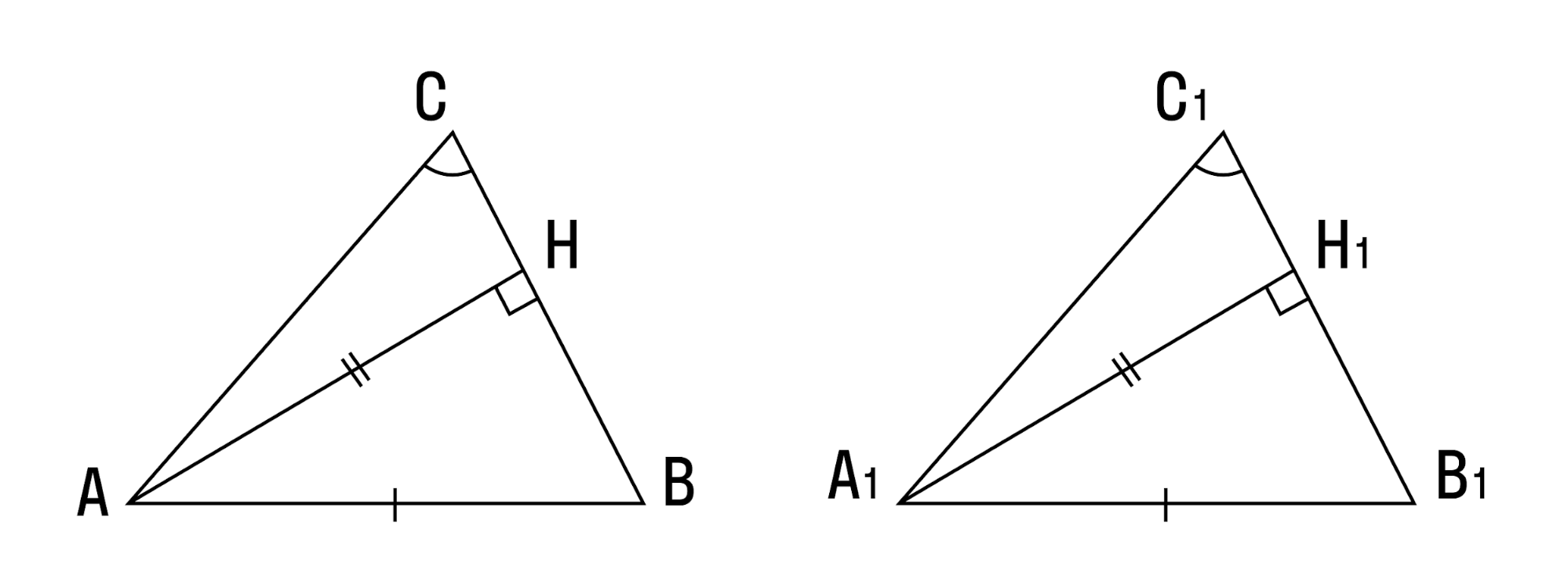
1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
   
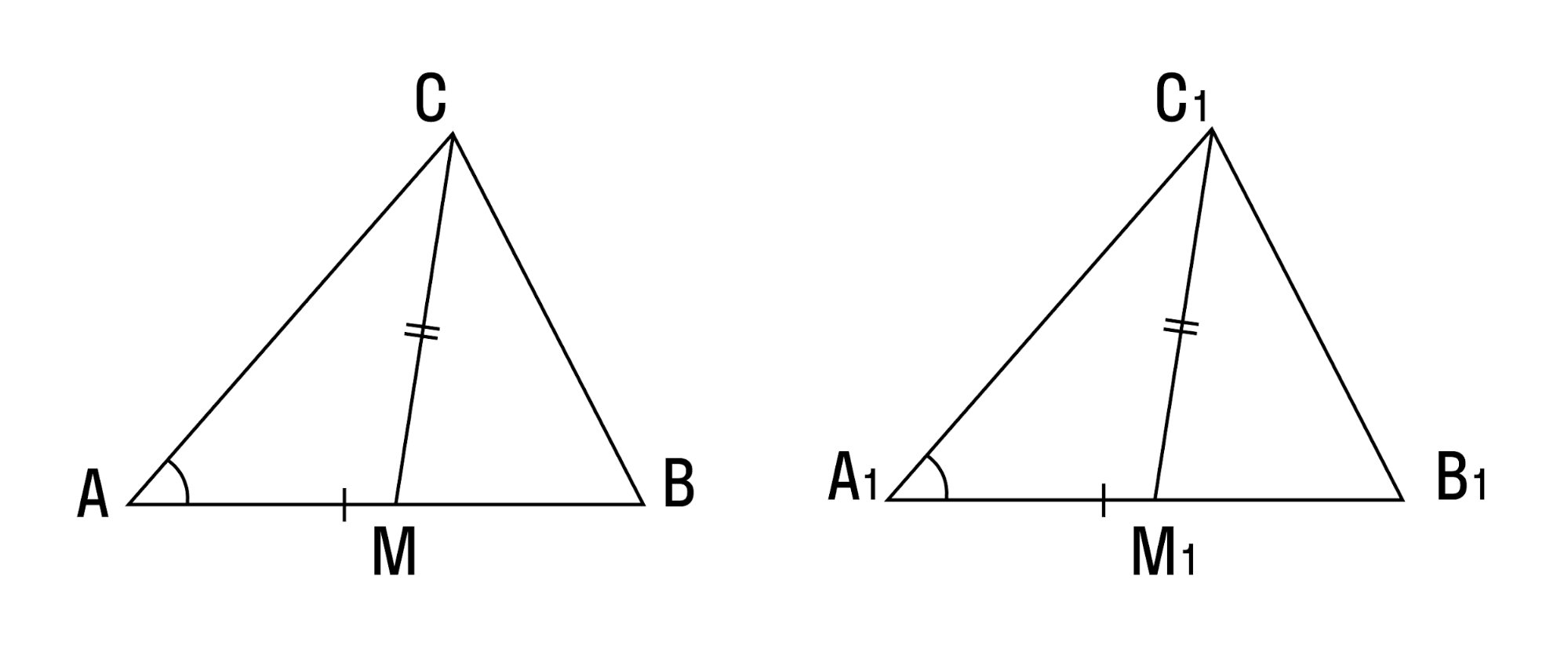
2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
   
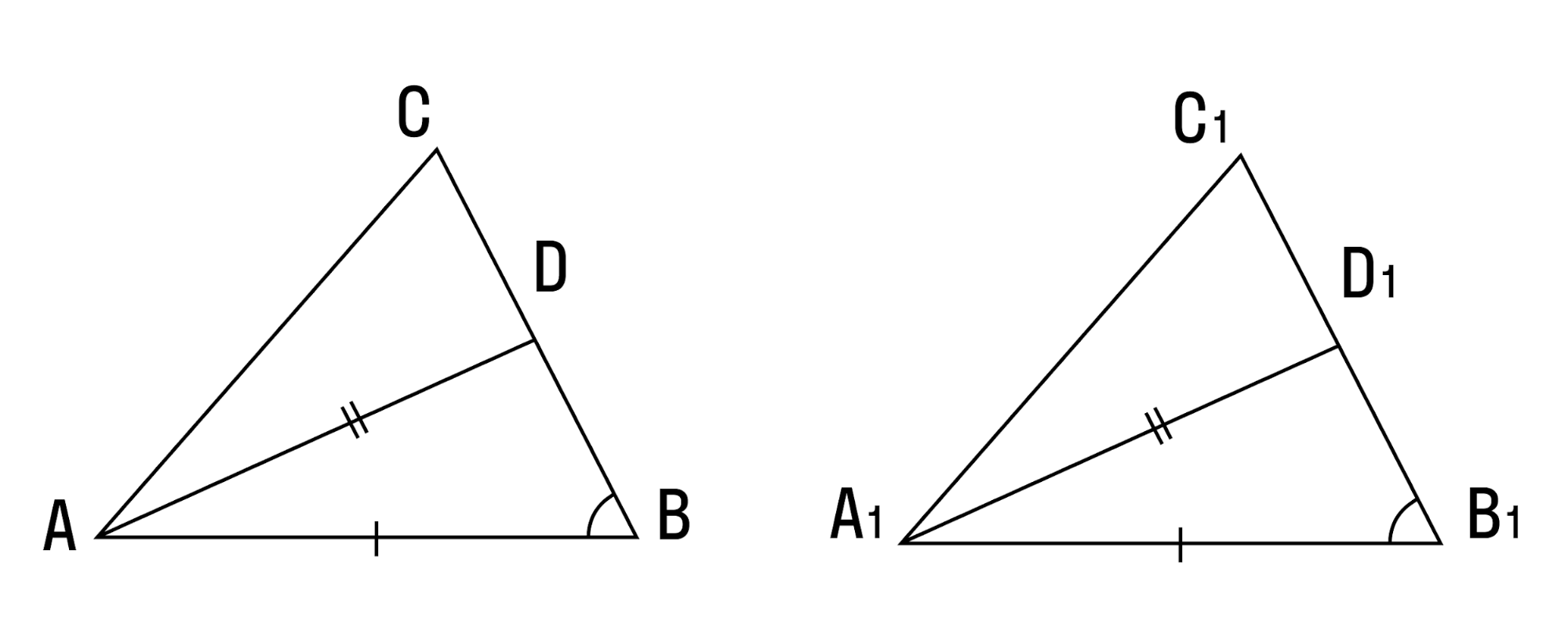
3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
   
4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
   
5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
   

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Видео:Построение медианы в треугольникеСкачать

Треугольники. Признаки равенства треугольников

Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .

Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.

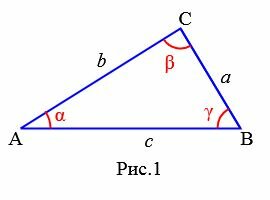Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.

Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.

Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A₁B₁C₁. Треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.

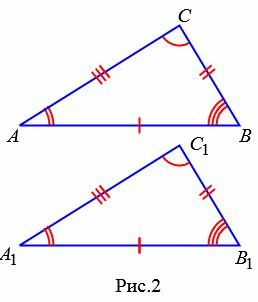Вышеизложенное можно сформулировать так:

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A₁B₁C₁ обозначается так:

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

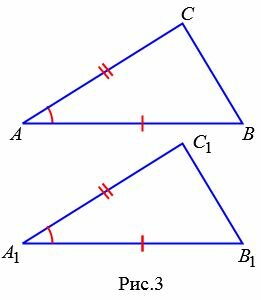Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и ∠A=∠A₁. Докажем, что .

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

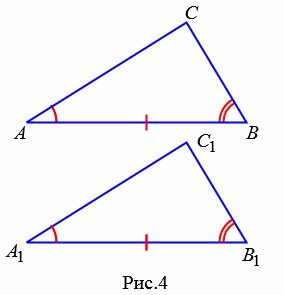Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁. Докажем, что .

Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

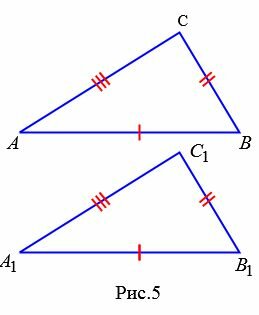Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

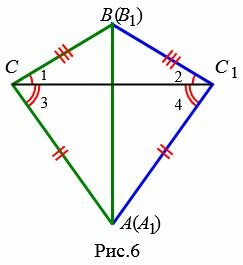Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

.

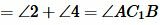Имеем AC=A₁C₁, BC=B₁C₁ ∠ACB=∠A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

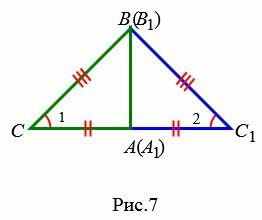Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда ∠1=∠2. Имеем: AC=A₁C₁, BC=B₁C₁, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.

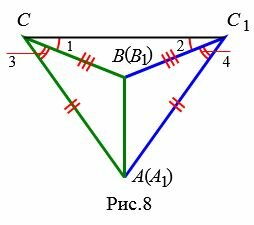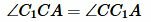
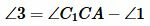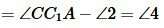Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и и, следовательно:

.

Имеем AC=A₁C₁, BC=B₁C₁ 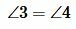и по первому признаку равенства треугольников . Теорема доказана.

Видео:Задача, которую исключили из экзамена в АмерикеСкачать

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

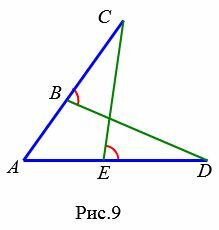Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства .

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

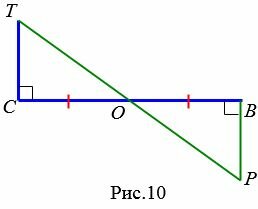Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .

🔍 Видео

Виды треугольниковСкачать

Признаки равенства треугольников. 7 класс.Скачать

Найдите третью сторону треугольникаСкачать

Первый признак равенства треугольников. 7 класс.Скачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Теорема о трёх медианахСкачать

МЕРЗЛЯК-7 ГЕОМЕТРИЯ. КОНТРОЛЬНАЯ РАБОТА -2. ТРЕУГОЛЬНИКИСкачать