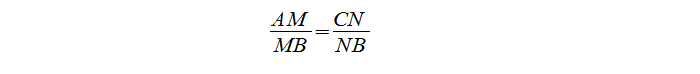Δ Σ Ψ Ω α β γ δ ε η θ λ μ ν ξ π ρ σ τ υ φ χ ψ ω
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
a b c d e f g h i j k l m n o p q r s t u v w x y z
≤ меньше или равно
≥ больше или равно
≈ приблизительно равно (асимптотически равно)
≅ approximately equal to
Греческие заглавные
Греческие строчные
Математические
знаки и символы
≤ меньше или равно
≥ больше или равно
≈ приблизительно равно (асимптотически равно)
≡ тождественно, совпадает с
√ квадратный корень (радикал)
∏ произведение последовательности — знак произведения
∅ пустое множество; диаметр **
∧ логическое И — wedge
∨ логическое ИЛИ — vee
∼ знак тильда — ‘изменяется с’ — знак подобия
- Знак подобия в геометрии — правило и примеры обозначения
- Определение и знак подобия в геометрии
- Коэффициент подобия треугольников и знак подобия
- Признаки подобия прямоугольных треугольников
- Доказательство подобия треугольников через среднюю линию
- Примеры решения задач по геометрии на тему «Подобие треугольников»
- Знак подобия в геометрии — правило и примеры обозначения
- Определение и знак подобия в геометрии
- Коэффициент подобия треугольников и знак подобия
- Признаки подобия прямоугольных треугольников
- Доказательство подобия треугольников через среднюю линию
- Примеры решения задач по геометрии на тему «Подобие треугольников»
- 💡 Видео
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Знак подобия в геометрии — правило и примеры обозначения
В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Определение и знак подобия в геометрии
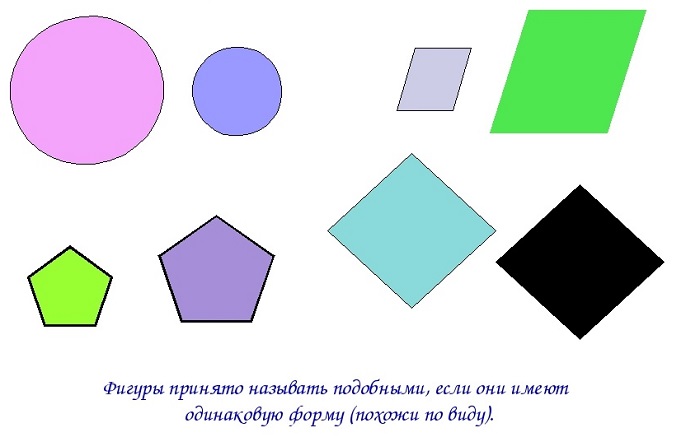
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Видео:8 класс, 23 урок, Второй признак подобия треугольниковСкачать

Коэффициент подобия треугольников и знак подобия
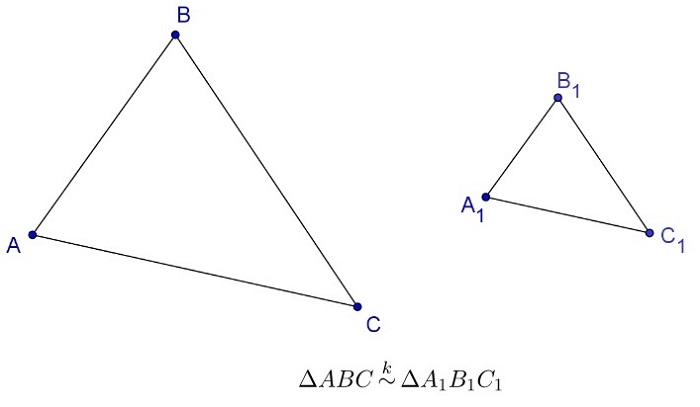
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком
обозначают логическую операцию «эквиваленция».
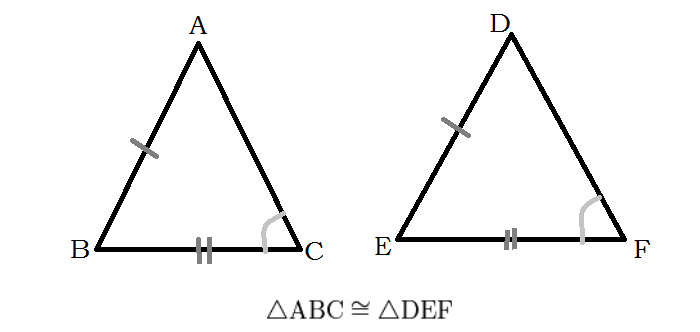
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
Видео:Первый признак подобия треугольников. Найти подобные по рисунку. Задачи на подобиеСкачать

Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
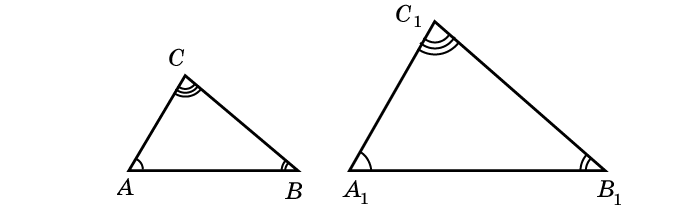
треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
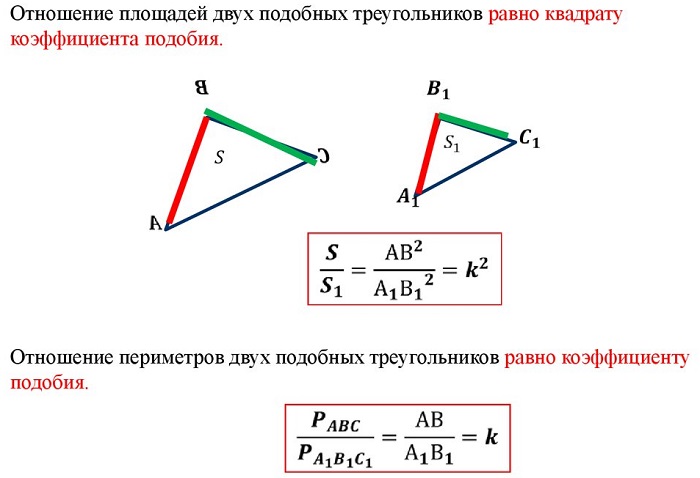
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Доказательство подобия треугольников через среднюю линию
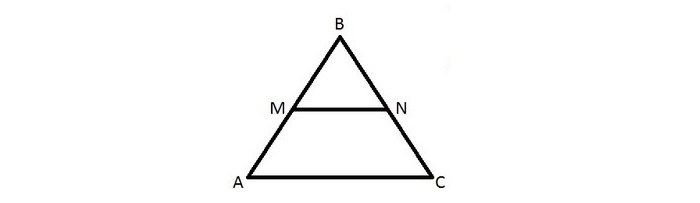
Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
Отсюда делаем вывод, что ∆MBN
∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Видео:Подобие треугольниковСкачать

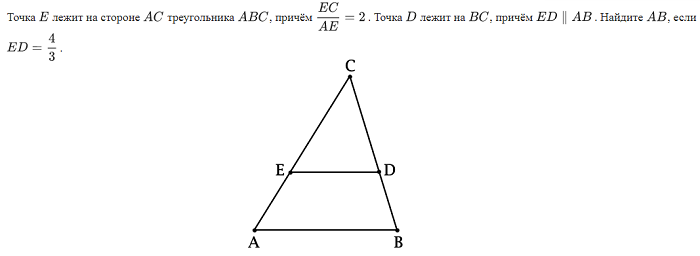
Примеры решения задач по геометрии на тему «Подобие треугольников»
Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Знак подобия в геометрии — правило и примеры обозначения
В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Определение и знак подобия в геометрии
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
∆A 1 B 1 C 1
— треугольники ABC и A1B1C1
подобны.
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком
обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
Видео:8 класс, 27 урок, Практические приложения подобия треугольниковСкачать

Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Видео:ПОДОБНЫЕ ТРЕУГОЛЬНИКИ коэффициент подобия 8 классСкачать

Доказательство подобия треугольников через среднюю линию
Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
Отсюда делаем вывод, что ∆MBN
∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Примеры решения задач по геометрии на тему «Подобие треугольников»
💡 Видео
Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

Геометрия 8 класс. Третий признак подобия треугольниковСкачать

8 класс, 24 урок, Третий признак подобия треугольниковСкачать

Геометрия . Задачи на подобие треугольников. Изи.Скачать

Первый признак подобия треугольников - геометрия 8 классСкачать

Первый признак подобия треугольниковСкачать

Геометрия 8 класс. Первый признак подобия треугольниковСкачать
Геометрия 8 класс (Урок№15 - Признаки подобия треугольников.)Скачать