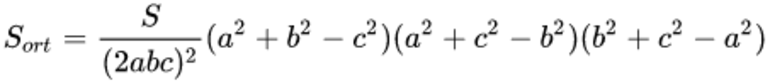Замечательные точки треугольника ортоцентр (5 видео)

Точка пересечения высот треугольника — свойства, координаты и расположение ортоцентра

Содержание

Что такое высота
Свойства ортоцентра
Полезные факты
Задача Фаньяно
История изучения
Ортоцентр.
Исследовательский проект Замечательные точки треугольника
Выберите документ из архива для просмотра:
🌟 Видео

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Что такое высота

Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.

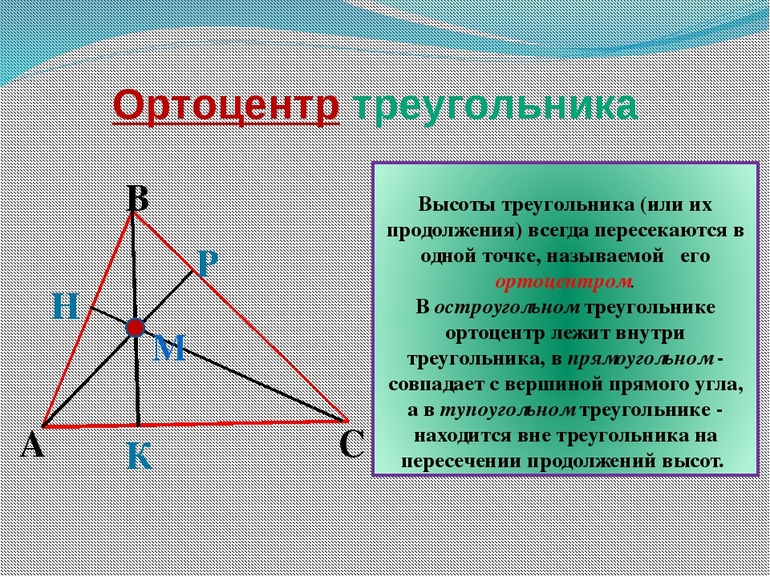
У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Свойства ортоцентра

Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.

Ортоцентр по отношению к фигуре может быть расположен:

внутри;
снаружи;
в вершине (у прямоугольных треугольников)

Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.

Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:

Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок. В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.

Полезные факты

Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.

Пусть:

H — ортоцентр в ABC;
О — центр описанной окружности.

Тогда:

окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
отрезок BH вдвое длиннее отрезка АС;
середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.

Задача Фаньяно

Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.

Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.

Площадь ортотреугольника рассчитывается по формуле:

Здесь S — площадь, а, b, c — стороны.

Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

История изучения

Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».

Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.

В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха. Она состоит из оснований медиан, высот и центров высот. Оказалось, что все эти точки лежат на общей окружности, центр которой находится на линии Эйлера.

Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.

Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.

Видео:Точка пересечения высот треугольника - Ортоцентр. ИЗИ ЗАДАЧАСкачать

Ортоцентр.

Ортоцентр — точка пересечения прямых, содержащих высоты треугольника.

Ортоцентр остроугольного треугольника лежит внутри треугольника.

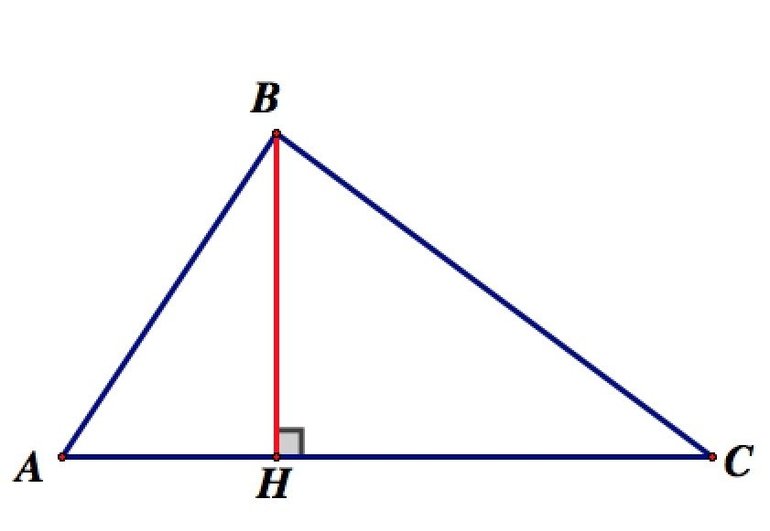
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

Ортоцентр тупоугольного треугольника лежит вне треугольника.

Свойства:

Точка, симметричная ортоцентру относительно стороны треугольника, лежит на описанной около него окружности.
Точка, симметричная ортоцентру относительно середины стороны треугольника, лежит на описанной окружности и диаметрально противоположна вершине треугольника, противолежащей стороне.
Расстояние от вершины треугольника до ортоцентра в два раза больше расстояния от центра описанной окружности до противолежащей стороны.
Сумма квадратов расстояния от вершины треугольника до ортоцентра и длины стороны, противолежащей этой вершине, равна квадрату диаметра описанной окружности.
Радиус описанной окружности, проведенный к вершине треугольника, перпендикулярен соответствующей стороне ортотреугольника.
При изогональном сопряжении ортоцентр переходит в центр описанной окружности.
Ортоцентр в остроугольном треугольнике является инцентром ортотреугольника.
Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих равные радиусы описанных окружностей. При этом одинаковый радиус этих трех окружностей равен радиусу окружности, описанной около исходного остроугольного треугольника.

Видео:№16 ЕГЭ 2023 по математике. Свойство ортоцентра за 5 минут. Четко и без водыСкачать

Исследовательский проект Замечательные точки треугольника

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Kurchavov_Alexandr-1.doc

Глава1. Исторические сведения о замечательных точках треугольника

1.2. Медианы треугольника

1.3. Биссектрисы треугольника

1.4. Высоты в треугольнике

1.5. Серединные перпендикуляры к сторонам треугольника

Глава 2. Исследование замечательных точек треугольника.

Список использованной литературы

Геометрия — это раздел математики, который рассматривает различные фигуры и их свойства. Геометрия начинается с треугольника. Вот уже два с половиной тысячелетия треугольник является символом геометрии; но он не только символ, треугольник — атом геометрии.

В своей работе я рассмотрю свойства точек пересечения биссектрис, медиан и высот треугольника, расскажу о замечательных их свойствах и линиях треугольника.

К числу таких точек, изучаемых в школьном курсе геометрии, относятся:

а) точка пересечения биссектрис (центр вписанной окружности);

б) точка пересечения серединных перпендикуляров (центр описанной окружности);

в) точка пересечения высот (ортоцентр);

г) точка пересечения медиан (центроид).

Актуальность: расширить свои знания о треугольнике, свойствах его замечательных точек.

Цель: исследование треугольника на его замечательные точки, изучение их классификаций и свойств.

1. Изучить необходимую литературу

2. Изучить классификацию замечательных точек треугольника

3. Уметь строить замечательные точки треугольника.

4. Обобщить изученный материал для оформления буклета.

умение находить замечательные точки в любом треугольнике, позволяет решать геометрические задачи на построение.

Глава 1. Исторические сведения о замечательных точках треугольника

В четвертой книге «Начал» Евклид решает задачу: «Вписать круг в данный треугольник». Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга. Из решения другой задачи Евклида вытекает, что перпендикуляры, восстановленные к сторонам треугольника в их серединах, тоже пересекаются в одной точке – центре описанного круга. В «Началах» не говорится о том, что и три высоты треугольника пересекаются в одной точке, называемой ортоцентром (греческое слово «ортос» означает «прямой», «правильный»). Это предложение было, однако, известно Архимеду, Паппу, Проклу.

Четвертой особенной точкой треугольника является точка пересечения медиан. Архимед доказал, что она является центром тяжести (барицентром) треугольника. На вышеназванные четыре точки было обращено особое внимание, и начиная с XVIII века они были названы «замечательными» или «особенными» точками треугольника.

Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – «геометрии треугольника» или «новой геометрии треугольника», одним из родоначальников которой стал Леонард Эйлер. В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр, барицентр и центр описанной окружности лежат на одной прямой, названной позже «прямой Эйлера».

Треугольник — геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки — вершины треугольника, отрезки — стороны треугольника.

В А, В, С — вершины

АВ, ВС, СА — стороны

С каждым треугольником связаны четыре точки:

Точка пересечения медиан;

Точка пересечения биссектрис;

Точка пересечения высот.

Точка пересечения серединных перпендикуляров;

1.2. Медианы треугольника

Медина треугольника ― отрезок , соединяющий вершину треугольника с серединой противоположной стороны (Рисунок 1). Точка пересечения медианы со стороной треугольника называется основанием медианы.

Рисунок 1. Медианы треугольника

Построим середины сторон треугольника и проведем отрезки, соединяющую каждую из вершин с серединой противолежащей стороны. Такие отрезки называются медианой.

И вновь мы наблюдаем, что и эти отрезки пересекаются в одной точке. Если мы измерим длины получившихся отрезков медиан, то можно проверить еще одно свойство: точка пересечения медиан делит все медианы в отношении 2:1, считая от вершин. И еще, треугольник, который опирается на острие иглы в точке пересечения медиан, находится в равновесии! Точка, обладающая таким свойством, называется центром тяжести (барицентр). Центр равных масс иногда называют центроидом. Поэтому свойства медиан треугольника можно сформулировать так: медианы треугольника пересекаются в центре тяжести и точкой пересечения делятся в отношении 2:1, считая от вершины.

1.3. Биссектрисы треугольника

Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. У треугольника существуют три биссектрисы, соответствующие трём его вершинам (Рисунок 2).

Рисунок 2. Биссектриса треугольника

В произвольном треугольнике ABC проведем биссектрисы его углов. И вновь при точном построении все три биссектрисы пересекутся в одной точке D. Точка D – тоже необычная: она равноудалена от всех трех сторон треугольника. В этом можно убедиться, если опустить перпендикуляры DA 1, DB 1 и DC1 на стороны треугольника. Все они равны между собой: DA1=DB1=DC1.

Если провести окружность с центром в точке D и радиусом DA 1, то она будет касаться всех трех сторон треугольника (то есть будет иметь с каждым из них только одну общую точку). Такая окружность называется вписанной в треугольник. Итак, биссектрисы углов треугольника пересекаются в центре вписанной окружности.

1.4. Высоты в треугольнике

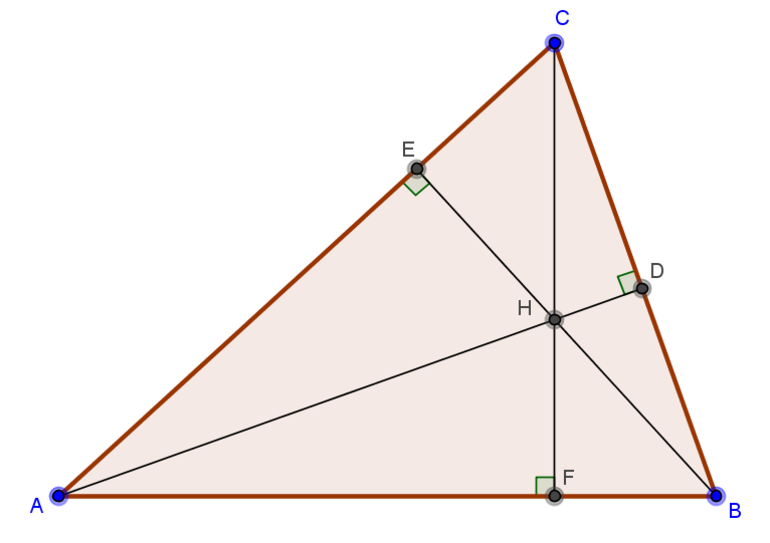
Высота треугольника — перпендикуляр , опущенный из вершины треугольника на противоположную сторону или прямую, совпадающую с противоположной стороной. В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника (Рисунок 3).

Рисунок 3. Высоты в треугольниках

Если в треугольнике построить три высоты, то все они пересекутся в одной точке H. Эта точка называется ортоцентром. (Рисунок 4).

С помощью построений можно проверить, что в зависимости от вида треугольника ортоцентр располагается по – разному:

у остроугольного треугольника – внутри;

у прямоугольного – на гипотенузе;

у тупоугольного – снаружи.

Рисунок 4. Ортоцентр треугольника

Таким образом, мы познакомились еще с одной замечательной точкой треугольника и можем сказать, что: высоты треугольника пересекаются в ортоцентре.

1.5. Серединные перпендикуляры к сторонам треугольника

Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.

Начертим произвольный треугольник ABC и проведем серединные перпендикуляры к его сторонам. Если построение выполнено точно, то все перпендикуляры пересекутся в одной точке – точке О. Эта точка равноудалена от всех вершин треугольника. Другими словами, если провести окружность с центром в точке О, проходящую через одну из вершин треугольника, то она пройдет и через две другие его вершины.

Окружность, проходящая через все вершины треугольника, называется описанной около него. Поэтому установленное свойство треугольника можно сформулировать так: серединные перпендикуляры к сторонам треугольника пересекаются в центре описанной окружности (Рисунок 5).

Рисунок 5. Треугольник вписанный в окружность