Задачи с разносторонним треугольником (8 видео)

ЕГЭ для VIP

Подготовке к ЕГЭ

Содержание

ЕГЭ по математике Профиль. Задание 3
ЕГЭ Профиль. Задание № 3
АЛГОРИТМ ВЫПОЛНЕНИЯ
Задачи на Прямоугольные треугольники
Задачи на Равнобедренные треугольники
Задачи на Разносторонние треугольники
Задачи на Параллелограммы
Задачи на Трапецию
Задачи на Центральные и вписанные углы
Задачи на Вписанные и описанные окружности
Тренировочные задания с самопроверкой
Треугольник. Формулы определения и свойства треугольников.
Определение треугольника
Классификация треугольников
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Свойства треугольника
1.Свойства углов и сторон треугольника.
2.Теорема синусов.
3. Теорема косинусов.
4. Теорема о проекциях
Медианы треугольника
Свойства медиан треугольника:
Формулы медиан треугольника
Задачи с разносторонним треугольником
Запомните!
Простые вопросы по теме «Треугольники»
Непростые вопросы по теме «Треугольники»
Ответы на простые и непростые вопросы
📹 Видео

Видео:ГЕОМЕТРИЯ 7 класс : Решение задач по теме "Равнобедренный треугольник"Скачать

ЕГЭ по математике Профиль. Задание 3

ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

ЕГЭ Профиль. Задание № 3

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 3 рассчитано на умение использовать геометрические понятия и теоремы для решения практических задач, связанных с нахождением геометрических величин (длин, углов, площадей).

Задание состоит из текстовой задачи и рисунка. Необходимо внимательно прочитать текст, решить задачу и записать результат в поле ответа в тексте работы и бланк ответов. Если в итоге получилась обыкновенная дробь, её нужно перевести в десятичную.

Чтобы успешно справиться с данным заданием, нужно повторить определения и свойства плоских фигур:

треугольники:
четырёхугольники, в частности параллелограмм, прямоугольник, ромб, квадрат, трапеция;
многоугольники, в частности правильные многоугольники;
окружность и круг, описанные и вписанные в многоугольник окружности;
площади треугольника, параллелограмма, трапеции, круга, сектора.

План выполнения:

Внимательно прочитайте задачу.
При необходимости выполните на чертеже дополнительные построения.
Выполните арифметические вычисления.
Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Задачи на Прямоугольные треугольники

При подготовке следует повторить значение синуса, косинуса и тангенса основных углов; отношения между сторонами прямоугольника; теорему Пифагора.

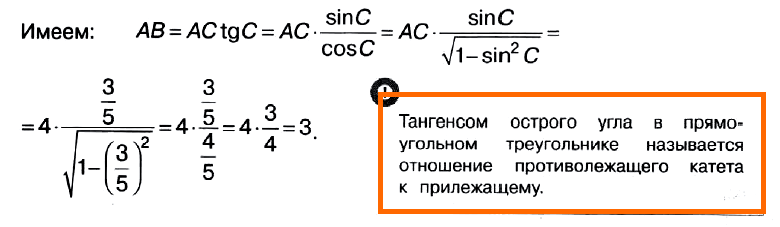
Задача № 3 (1). В треугольнике АВС угол А равен 90°, АС = 4, sin C = 3/5. Найдите АВ.

Решение:

Ответ: 3.

Задача № 3 (2). В треугольнике АВС угол С равен 90°, CD – высота, АВ = 5, tg B = 1/2. Найдите BD.

Решение: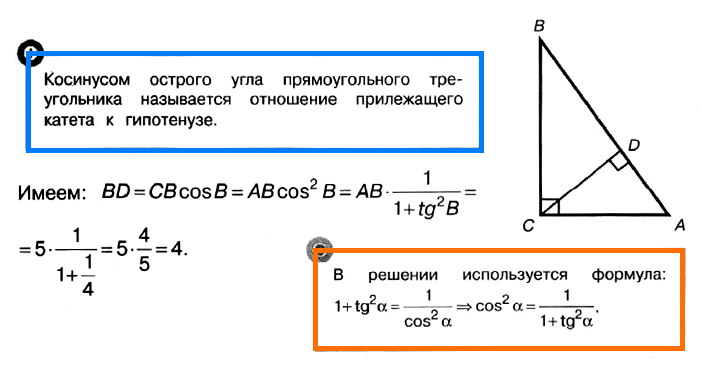

Ответ: 4.

Задачи на Равнобедренные треугольники

Задача № 3 (3). В треугольнике АВС АС = ВС = 10, sin А = 3/5. Найдите АВ.

Решение:

Ответ: 16.

Задача № 3 (4). В треугольнике АВС АС = ВС = 25, sin BAC = 3/5. Найдите высоту АН.

Решение:

Ответ: 24.

Задача № 3 (5). В тупоугольном треугольнике АВС АС = ВС = 6, высота АН = 3. Найдите sin АСВ.

Решение: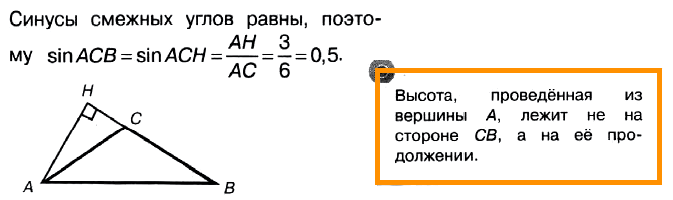

Ответ: 0,5.

Задачи на Разносторонние треугольники

Задача № 3 (6). Площадь треугольника АВС равна 8. DE — средняя линия CDE.

Решение:

Ответ: 2.

Задача № 3 (7). В треугольнике АВС угол С равен 60°, AD и BE — биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах.

Решение: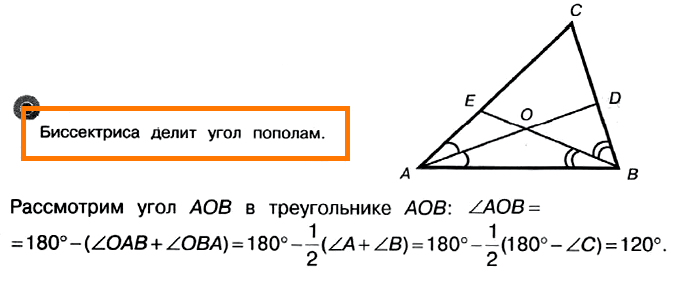

Ответ: 120.

Задачи на Параллелограммы

Задача № 3 (8). Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

Решение: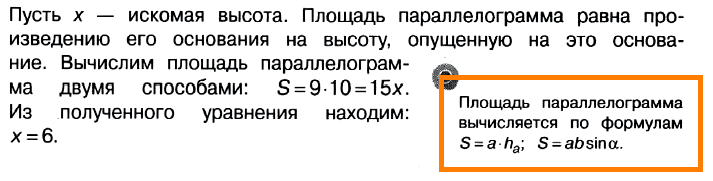

Ответ: 6.

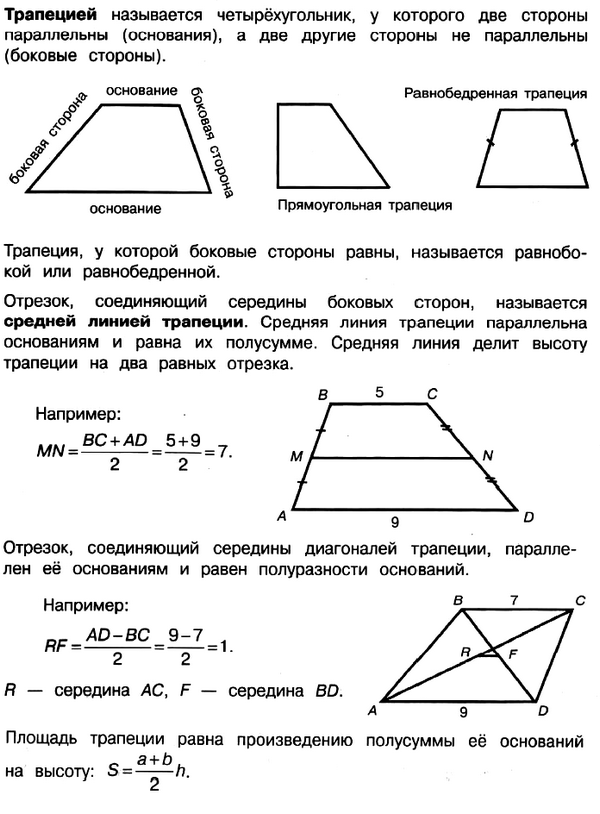
Задачи на Трапецию

Задача № 3 (9).

Решение: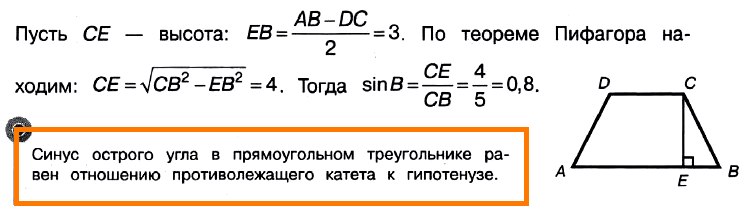

Ответ: 0,8.

Задачи на Центральные и вписанные углы

При подготовке нужно повторить свойства центральных и вписанных углов, понятия хорды, касательной и секущей к окружности; знать правила нахождения величин центральных и вписанных углов, дуг окружностей.

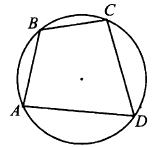
Задача № 3 (10). Найдите угол АСВ, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно 158° и 38°. Ответ дайте в градусах.

Решение:

Ответ: 60.

Задачи на Вписанные и описанные окружности

Задача № 3 (11). В четырёхугольник ABCD вписана окружность, АВ = 4, CD = 6. Найдите периметр четырёхугольника ABCD.

Решение:

Ответ: 20.

Задача № 3 (12).

Решение:

Ответ: 1.

Тренировочные задания с самопроверкой

№ 3.1. Стороны АВ, ВС, CD и AD четырёхугольника ABCD стягивают дуги описанной окружности, градусные величины которых равны соответственно 75°, 63°, 93°, 129° (см. рис.). Найдите угол BCD. Ответ дайте в градусах.

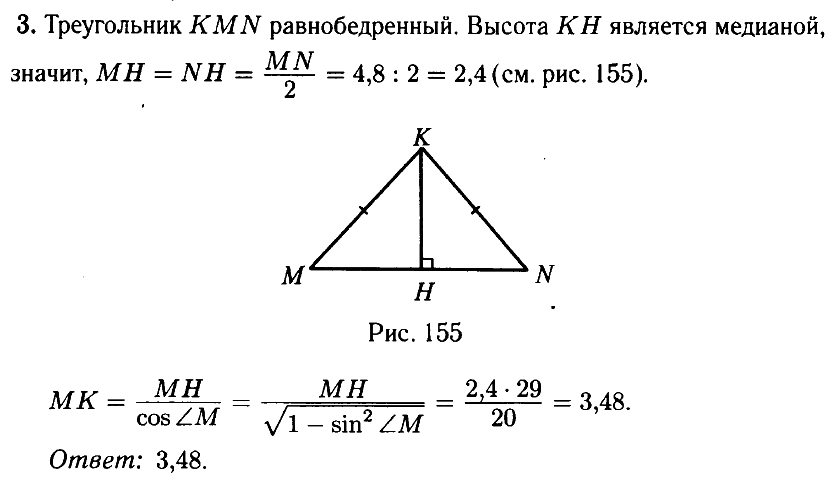
№ 3.2. В треугольнике MNK известно, что МК = NK, MN = 4,8, sin М = 21/29 (см. рис.). Найдите МК.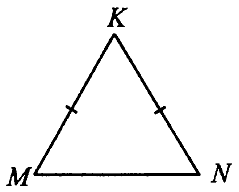

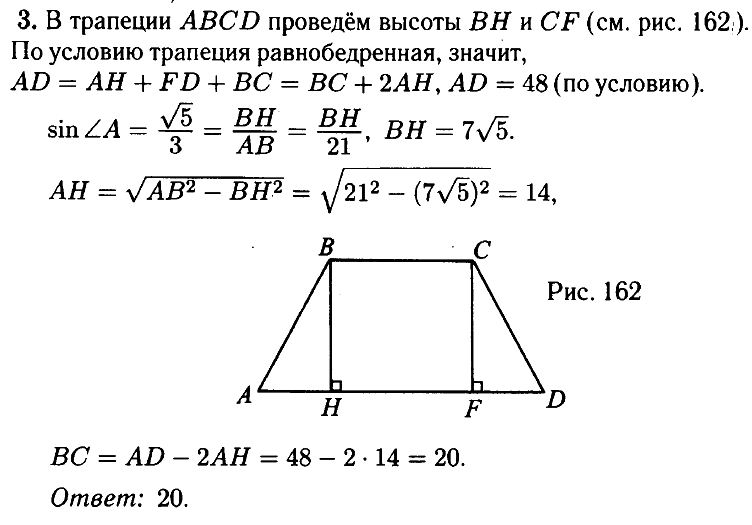
№ 3.3. Большее основание равнобедренной трапеции равно 48. Боковая сторона равна 21. Синус острого угла равен √5/3 (см. рис.). Найдите меньшее основание.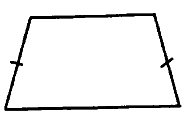

№ 3.4. В треугольнике АВС известно, что АС = ВС, высота ВН равна 9, АВ = 3√13 (см. рис.). Найдите tg АВС.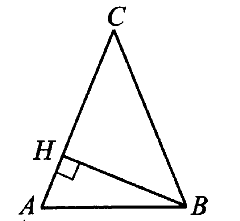

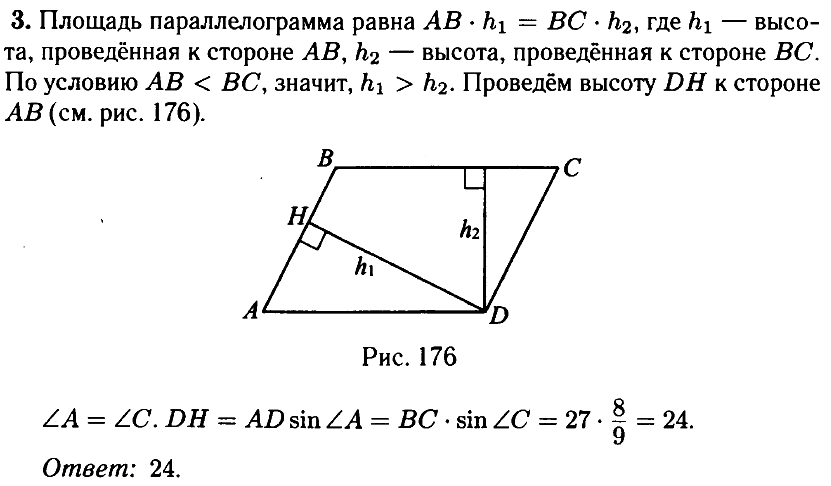
№ 3.5. В параллелограмме ABCD известно, что АВ = 18, ВС = 27, sin ∠C = 8/9 (см. рис.). Найдите большую высоту параллелограмма.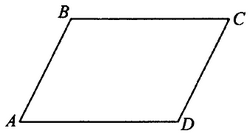

Вы смотрели: ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Видео:Треугольники. Практическая часть - решение задачи. 7 класс.Скачать

Треугольник. Формулы определения и свойства треугольников.

В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.

Содержание:

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Определение треугольника

Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.

Треугольник ABC (△ABC)

Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.

Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Классификация треугольников

Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.

1.Разносторонний – треугольник, у которого все стороны имеют разную длину.

2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β

3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°

5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Свойства треугольника

1.Свойства углов и сторон треугольника.

Сумма всех углов треугольника равна 180°:

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

2.Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c
sin α	=	sin β	=	sin γ

3. Теорема косинусов.

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

4. Теорема о проекциях

Для остроугольного треугольника:

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Медианы треугольника

Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)

2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

AO	=	BO	=	CO	=	2
OD	=	OE	=	OF	=	1

3. Медиана треугольника делит треугольник на две равновеликие по площади части

4. Треугольник делится тремя медианами на шесть равновеликих треугольников.

5. Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника

Формулы медиан треугольника через стороны:

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Задачи с разносторонним треугольником

Наглядная геометрия 7 класс. Ключевые задачи по теме Треугольники

Запомните!

1. Признаки равенства треугольников.

1-й. По двум сторонам и углу между ними.
2-й. По стороне и двум прилежащим к ней углам.
3-й. По трем сторонам.

2. Свойство углов равнобедренного треугольника.

Углы при основании равнобедренного треугольника равны.

3. Обратная теорема.

Если два угла треугольника равны, то треугольник равнобедренный.

4. Свойство биссектрисы равнобедренного треугольника.

Биссектриса, высота и медиана равнобедренного треугольника, проведенные из вершины к основанию, совпадают.

5. Признаки равнобедренного треугольника. Треугольник является равнобедренным, если:

а) высота является и медианой;
б) высота является и биссектрисой;
в) биссектриса является и медианой.

6. Теорема о свойстве точек серединного перпендикуляра.

Любая точка серединного перпендикуляра равноудалена от концов отрезка.
Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к нему.

7. Теорема о пересечении серединных перпендикуляров.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке — центре описанной около треугольника окружности.

Простые вопросы по теме «Треугольники»

В треугольнике провели медиану. Сколько треугольников изображено на рисунке?
Если стороны треугольника продлить, то сколько углов всего образуется, не считая развернутых? А считая и развернутые?
Верно ли, что биссектриса треугольника лежит на биссектрисе угла?
Может ли высота треугольника делить сторону пополам?
Может ли биссектриса треугольника быть перпендикулярной стороне треугольника?
Верно ли утверждение: «Биссектриса равнобедренного треугольника является высотой и медианой»?
Является ли любой равнобедренный треугольник равносторонним?
Является ли любой равносторонний треугольник равнобедренным?
Может ли биссектриса некоторого равнобедренного треугольника, проведенная к боковой стороне, быть медианой?
Может ли высота треугольника быть равна его медиане, проведенной из той же вершины?
Может ли биссектриса треугольника быть равна его высоте, проведенной из той же вершины?
Существует ли треугольник, периметр которого в 3 раза больше одной из сторон?
Если медиана образует равные углы с соседними сторонами треугольника, то какой угол она образует с третьей стороной?
Что для студентов означает слово «медиум»?
Сколько всего теорем в данной теме?

Непростые вопросы по теме «Треугольники»

16* В треугольнике провели 2 медианы. Сколько треугольников изображено на рисунке?
17* В треугольнике провели 3 медианы. Сколько треугольников изображено на рисунке?
18* Может ли в треугольнике высота являться медианой, но не являться биссектрисой?
19* Как звучит теорема о свойстве углов равнобедренного треугольника в форме «Если …, то …»?
20* Как звучит утверждение, обратное теореме о свойстве углов равнобедренного треугольника, в форме «Если …, то …»?
21* Может ли медиана треугольника равняться соседней стороне?
22* Может ли биссектриса треугольника равняться соседней стороне?
23* Может ли высота треугольника равняться соседней стороне?
24* Может ли серединный перпендикуляр к стороне треугольника иметь общую точку с каждой из двух других сторон?
25* Может ли серединный перпендикуляр к стороне треугольника делить противоположный угол треугольника пополам?

Ответы на простые и непростые вопросы

Три. Два маленьких и один данный.
12; 24.
Да.
Да. В равнобедренном треугольнике.
Да. В равнобедренном треугольнике.
Нет. Только биссектриса, проведенная из вершины к основанию.
Нет.
Да.
Да. Если треугольник равносторонний.
Да. В равнобедренном треугольнике это высота, проведенная к его основанию.
Да. В равнобедренном треугольнике это биссектриса, проведенная к его основанию.
Да. Например, равносторонний.
90°. Если медиана является биссектрисой, то треугольник равнобедренный и эта медиана является и высотой, проведенной к основанию.
Медиум — студенческий праздник, знаменующий середину учебы.
Тринадцать теорем, включая задачу о пересечении серединных перпендикуляров к сторонам треугольника.

16* 8.
17* 16.
18* Нет. Если высота является медианой, то треугольник равнобедренный и эта высота является и биссектрисой.
19* «Если треугольник равнобедренный, то углы при основании равны». 20* «Если у треугольника два угла равны, то треугольник равнобедренный».
21* Да.
22* Да.
23* Да. В прямоугольном треугольнике.
24* Да. В равнобедренном прямоугольном треугольнике.
25* Да. Если треугольник равнобедренный.

Это конспект по геометрии «Ключевые задачи по теме Треугольники». Выберите дальнейшие действия: