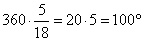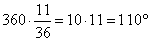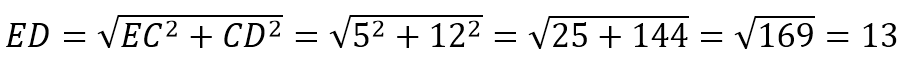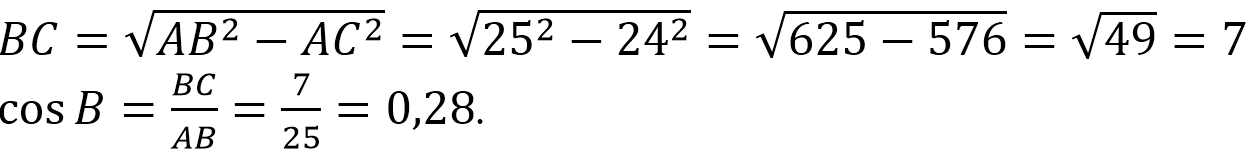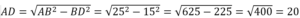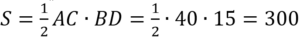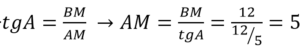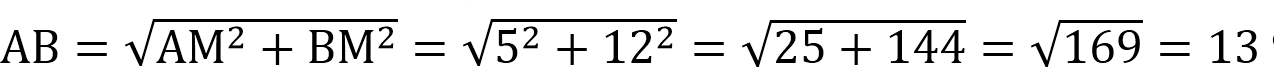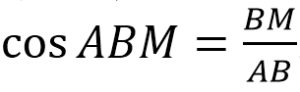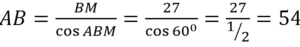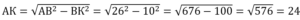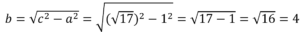Задача в равнобедренном треугольнике авс

Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».

Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]

Стоимость занятий

Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.

Видеокурсы подготовки к ЕГЭ-2021

Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.

Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.

Видео:№240. В равнобедренном треугольнике ABC с основанием АС биссектрисы углов А и С пересекаютсяСкачать

Группа Вконтакте

В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.

Видео:[ОГЭ] В равнобедренном треугольнике ABC с основанием АС внешний угол при вершине С равен 123°Скачать

Преимущества

Педагогический стаж

Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.

Собственная методика

За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.

Гарантированный результат

За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.

Индивидуальная работа

Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

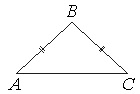
Задача в равнобедренном треугольнике авс

Основная дидактическая цель урока: совершенствовать навыки решения задач на применение второго признака равенства треугольников. Перед решением задач необходимо повторить конспекты: «Треугольник. Равенство треугольников», «ЗАДАЧИ на Признаки равенства треугольников».

I уровень сложности (легкий)

Вариант 1 (уровень 1)

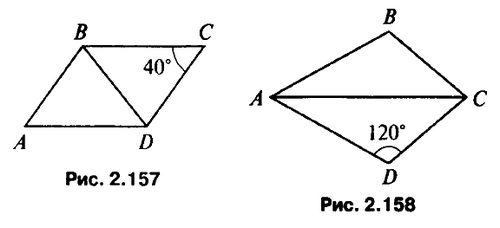
1. Дано: АВ = СD, ВС = DA, ∠C = 40° (рис. 2.157).
   Доказать: ΔABD = ΔCDB. Найти: ∠A.
2. На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – медиана треугольника. Докажите, что MD = ND.
3. В треугольниках АВС и А₁В₁С₁ АВ = А₁В₁, ∠A = ∠A₁, ∠B = ∠B₁. Точки D и D₁ лежат соответственно на сторонах АС и А₁С₁, причем CD = C₁D₁. Докажите, что ΔBDC = ΔB₁D₁C₁. Сравните отрезки BD и B₁D₁.

Вариант 2 (уровень 1)

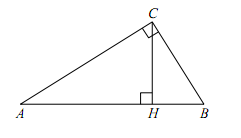
1. Дано: AD = АВ, CD = CB, D= 120° (рис. 2.158).
   Доказать: ΔDAC = ΔBAC. Найти: ∠B.
2. На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки ВМ и BN. BD – высота треугольника. Докажите, что MD = ND.
3. В треугольниках АВС и А₁В₁С₁ АВ = A₁B₁, АС = A₁C₁, ∠A = ∠A₁. Точки D и D₁ лежат соответственно на сторонах АС и A₁C₁, ∠DBC = ∠D₁B₁C₁. Докажите, что ΔBDC = ΔB₁D₁C₁. Сравните углы ВDC и B₁C₁D₁.

II уровень сложности (средний)

Вариант 1 (уровень 2)

1. Дано: АВ = СD, ВС = AD (рис. 2.159). Доказать: ∠A = ∠C.
2. На боковых сторонах равнобедренного треугольника АВС с основанием АС отложены равные отрезки AM и CN. BD, медиана ΔAВС, пересекает отрезок MN в точке О. Докажите, что ВО – медиана ΔMBN.
3. В треугольниках АВС и А₁В₁С₁ АВ = A₁B₁, ∠А = ∠A₁, ∠B = ∠B₁. На сторонах ВС и В₁С₁ отмечены точки D и D₁ так, что ∠CAD = ∠C₁A₁D₁. Докажите, что: а) ΔADC = ΔA₁D₁C₁; б) ΔADB = ΔA₁D₁B₁.

Вариант 2 (уровень 2)

1. Дано: АВ = AD, ВС = DC (рис. 2.162). Доказать: ∠B = ∠D.
2. Дан равнобедренный ΔАВС с основанием АС и высотой BD. На лучах ВА и ВС вне треугольника АВС отложены равные отрезки AM и CN. Луч BD пересекает отрезок MN в точке О. Доказать, что ВО – высота ΔMBN.
3. В треугольниках DEC и D₁E₁C₁ DE = D₁E₁, ∠D = ∠D₁, ∠E = ∠E₁. На сторонах DE и D₁E₁ отмечены точки P и P₁ так, что ∠DCP = ∠D₁C₁P₁. Докажите, что: a) ΔDCP = ΔD₁C₁P₁; б) ΔCPE = ΔC₁P₁E₁.

III уровень сложности (сложный)

Вариант 1 (уровень 3)

1. Дано: АВ = CD, АС = BD (рис. 2.165). Доказать: ∠CAD = ∠BDA.
2. ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ME = PF. Докажите, что луч KN – биссектриса угла EKF (рис. 2.166).
3. В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно – так, что ВМ = BN. Докажите, что ΔBDM = ΔBDN.

Вариант 2 (уровень 3)

1. Дано: АВ = CD, АС = BD (рис. 2.168). Доказать: ∠ACB = ∠DBC.
2. ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ∠MKE = ∠PKF. Докажите, что ΔNЕК = ΔNFK (рис. 2.169).
3. В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне АВС отмечены точки М и N соответственно, так, что ∠BDM =∠BDN. Докажите, что ΔBDM = ΔBDN.

Самостоятельная работа № 6
Указания к решению и ОТВЕТЫ

С-6. I уровень сложности (ответы)

Геометрия 7 Атанасян Самостоятельная 6

С-6. II уровень сложности (ответы)

Задания и Ответы на Вариант 1 (уровень 2)

№ 1. Дано: АВ = СD, ВС = AD (рис. 2.159). Доказать: ∠A = ∠C.
Докажите самостоятельно.

№ 2. На боковых сторонах равнобедренного треугольника АВС с основанием АС отложены равные отрезки AM и CN. BD, медиана ΔAВС, пересекает отрезок MN в точке О. Докажите, что ВО – медиана ΔMBN.

Доказательство:
1) ΔАВС – равнобедренный с основанием АС, и медиана BD является его биссектрисой (рис. 2.160).
2) ΔMBN – равнобедренный с основанием MN, так как МВ = BN (МВ = ВА– МА; BN = ВС – МС, ВА = ВС, МА = NC). BD – биссектриса ΔMBN, и по свойству биссектрисы равнобедренного треугольника она является медианой, т. е. ВО – медиана ΔMBN.

Доказательство:
а) ΔАВС = ΔА₁В₁С₁ по стороне и прилежащим к ней углам (АВ = A₁B₁, ∠A = ∠A₁, ∠B = ∠B₁ по условию задачи) (рис. 2.161). ΔADC = ΔA₁D₁C₁ по стороне и прилежащим к ней углам (АС = А₁С₁, ∠C = ∠C₁ из равенства треугольников АВС и А₁В₁С₁, ∠CAD = ∠C₁A₁D₁ по условию задачи).
б) Так как ΔADC = ΔA₁D₁C₁, то DC = D₁C₁, следовательно, равны отрезки BD и B₁D₁ (ВС = В₁С₁ из равенства треугольников АВС и А₁В₁С₁). Так как АВ = А₁В₁, ∠B = ∠B₁ из равенства треугольников АВС и А₁В₁С₁ и BD = В₁D₁, то ΔABD = ΔA₁B₁D₁ по двум сторонам и углу между ними.

Задания и Ответы на Вариант 2 (уровень 2)

№ 1. Дано: АВ = AD, ВС = DC (рис. 2.162). Доказать: ∠B = ∠D.
Докажите самостоятельно.

№ 2. Дан равнобедренный ΔАВС с основанием АС и высотой BD. На лучах ВА и ВС вне треугольника АВС отложены равные отрезки AM и CN. Луч BD пересекает отрезок MN в точке О. Доказать, что ВО – высота ΔMBN.

Доказательство:
1) ΔАВС – равнобедренный с основанием АС, и высота BD, проведенная из его вершины к основанию, является и его биссектрисой, т. е. ВО – биссектриса ∠ABC и ∠MBN тоже (рис. 2.163).
2) ΔMBN – равнобедренный с основанием MN (ВМ = ВА + AM, BN = ВС + CN; так как ВА = ВС и АМ = CN, то ВМ = BN). В равнобедренном ΔMBN биссектриса ВО, проведенная из его вершины к основанию, является и его высотой.

Доказательство:
а) ΔDEC = ΔD₁E₁C₁ по стороне и прилежащим к ней углам (DE = D₁E₁, ∠D = ∠D₁, ∠E = ∠E₁) (рис. 2.164).
Так как ΔDEC = ΔD₁E₁C₁, то DC = D₁C₁. Тогда ΔDCP= ΔD₁C₁P₁ по стороне и прилежащим к ней углам (DC = D₁C₁, ∠D = ∠D₁, ∠PCD= ∠P₁C₁D₁).
б) Так как ΔDEC = ΔD₁E₁C₁, тo EC = E₁C₁, ∠ECD = ∠E₁C₁D₁.
Так как ∠ECD = ∠E₁C₁D₁, ∠PCD = ∠P₁C₁D₁, a ∠ECP = ∠ECD – ∠DCP, ∠E₁C₁P₁ = ∠E₁C₁D₁ – ∠D₁C₁P₁, ∠ECP = ∠E₁C₁P₁.
Так как ЕС = E₁C₁ ∠E = ∠E₁, ∠ECP = ∠E₁C₁P₁, то ΔPEC = ΔP₁E₁C₁ по стороне и прилежащим к ней углам.

Геометрия 7 Атанасян Самостоятельная 6.

С-6. III уровень сложности (ответы)

Задания и Ответы на Вариант 1 (уровень 3)

№ 1. Дано: АВ = CD, АС = BD (рис. 2.165). Доказать: ∠CAD = ∠BDA.
Докажите самостоятельно.

№ 2. ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ME = PF. Докажите, что луч KN – биссектриса угла EKF (рис. 2.166).

Доказательство: ΔМЕК = ΔPFK по двум сторонам и углу между ними (ME = FP, МК = КР по условию задачи, ∠M = ∠P как углы при основании равнобедренного ΔMNP). Следовательно, КЕ= KF.
ΔKEN = ΔKFN по трем сторонам (КЕ = KF; KN – общая сторона; NE = NF, так как NE = MN – ME, NF = PN – PF, a MN = PN, ME = PF). Следовательно, ∠EKN = ∠FKN.
Так как ∠EKN = ∠FKN, то KN – биссектриса угла ∠EKF.

№ 3. В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне треугольника АВС отмечены точки М и N соответственно – так, что ВМ = BN. Докажите, что ΔBDM = ΔBDN.

Доказательство: Так как D – середина основания равнобедренного ΔАВС с основанием АС, то BD – медиана, а значит, и биссектриса ΔАВС. Следовательно, ∠ABD = ∠CBD (рис. 2.167).
∠NBA = ∠CBM как вертикальные.
∠NBD = ∠NBA + ∠ABD, a ∠MBD = ∠MBC + ∠CBD. Так как ∠ABD = ∠CBD, ∠MBC = ∠NBA, то ∠NBD = ∠MBD.
ΔNBD = ΔMBD по двум сторонам и углу между ними (NB = МВ; BD – общая сторона; ∠NBD = ∠MBD).

Задания и Ответы на Вариант 2 (уровень 3)

№ 1. Дано: АВ = CD, АС = BD (рис. 2.168). Доказать: ∠ACB = ∠DBC.
Докажите самостоятельно.

№ 2. ΔMNP – равнобедренный с основанием МР, точка К – середина отрезка МР, ∠MKE = ∠PKF. Докажите, что ΔNЕК = ΔNFK (рис. 2.169).

Доказательство: ΔМЕК = ΔPFK по стороне и прилежащим к ней углам (МК = КР, так как К – середина МР; ∠MKE = ∠PKF по условию задачи; ∠M = ∠P как углы при основании равнобедренного ΔMNP).
Так как ΔМЕК = ΔPFK, то ME = PF, следовательно, EN = FN (EN = MN – ME, FN = PN – PF, a MN = FN как боковые стороны равнобедренного треугольника).
Так как ΔМЕК = ΔPFK, то КЕ = KF. ΔNEK = ΔNFK по трем сторонам (NK – общая сторона, NE = EF, ЕК = ЕК).

№ 3. В равнобедренном треугольнике АВС точка D – середина основания АС. На лучах АВ и СВ вне АВС отмечены точки М и N соответственно, так, что ∠BDM =∠BDN. Докажите, что ΔBDM = ΔBDN.

Доказательство: Так как D – середина основания АС равнобедренного ΔАВС, то BD – медиана и биссектриса ΔАВС. Следовательно, ∠ABD = ∠CBD (рис. 2.170).
∠NBA = ∠CBM как вертикальные. Поэтому ∠NBD = ∠MBD (∠NBD = ∠NBA + ∠ABD, ∠MBD = ∠MBC + ∠CBD, a ∠NBA = ∠CBM, ∠ABD = ∠CBD).
ΔBDM = ΔBDN по стороне и прилежащим к ней углам (BD – общая сторона, ∠NBD = ∠MBD, ∠BDM = ∠BDN).

Вы смотрели: Геометрия 7 класс (УМК Атанасян и др. — Просвещение). Урок 21. Решение задач на применение третьего признака равенства треугольников. Самостоятельная работа № 6 с ответами и решениями (3 уровня сложности по 2 варианта в каждом). Геометрия 7 Атанасян Самостоятельная 6. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

Видео:№235. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD. Найдите углыСкачать

Задание №15 ЕГЭ по математике базового уровня

Видео:№296. В равнобедренном треугольнике ABC биссектрисы равных углов B и С пересекаются в точке О. ДокажСкачать

Планиметрия

В задании № 15 базового уровня ЕГЭ по математике нас ждет решение задач по планиметрии. Задачи в этом разделе не сложные, достаточно знать определения основных понятий и базовые формулы, после чего задача сводится к элементарным вычислениям.

Разбор типовых вариантов заданий №15 ЕГЭ по математике базового уровня

Вариант 15МБ1

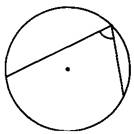
В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(смотрите рисунок). Найдите длину отрезка AH.

Алгоритм выполнения:

1. Вспомнить определение косинуса угла.
2. Записать выражение для нахождения косинуса угла.
3. Выразить неизвестную величину.
4. Вычислить.

Решение:

Вспомним определение косинуса угла.

Косинус – это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, прилежащего к острому углу, к гипотенузе.

Запишем выражение для нахождения косинуса угла. Для этого рассмотрим треугольник ACH.

Гипотенуза – это сторона прямоугольного треугольника, лежащая против угла 90°. В данном случае против угла H лежит сторона AC, то есть AC – гипотенуза.

Прилежащий к углу А катет – АН.

Получим cos A = АН/АС.

Выразим неизвестную величину.

АН = АС · cos A = 4 · 0,8 = 3,2

Вариант 15МБ2

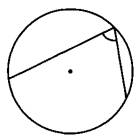
Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах.

Алгоритм выполнения:

1. Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
2. Вычислить градусную меру угла, на который опирается дуга.
3. Вычислить вписанный угол.

Решение:

Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.

Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.

Вычислим градусную меру угла, на который опирается дуга.

Весь круг составляет 360°, а 5/18 от его длины это

Вычислим вписанный угол.

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен

Вариант 15МБ3

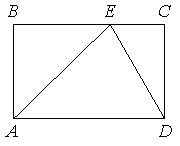
Найдите вписанный угол, опирающийся на дугу, длина которой равна 11/36 длины окружности. Ответ дайте в градусах.

Алгоритм выполнения:

1. Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
2. Вычислить градусную меру угла, на который опирается дуга.
3. Вычислить вписанный угол.

Решение:

Вспомним соотношение величины вписанного угла и градусной меры угла, на который он опирается.

Величина вписанного угла равна половине градусной меры дуги, на которую он опирается.

Вычислим градусную меру угла, на который опирается дуга.

Весь круг составляет 360°, а 11/36 от его длины это

Вычислим вписанный угол.

Так как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен

Вариант 15МБ4

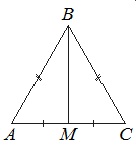
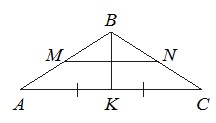
В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ.

Алгоритм выполнения

1. Определяем

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Решение:

Если АВ=ВС, то ∆АВС – равнобедренный.

В равнобедр.треугольнике медиана, опущенная на основание, является еще и высотой. Тогда угол АМВ=90 0 , и ∆АМВ – прямоугольный с катетами АМ и ВМ и гипотенузой АВ.

По т.Пифагора АМ 2 +ВМ 2 =АВ 2 . Отсюда: .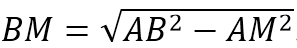

Т.к. АМ медиана, то

.

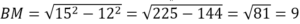
Вариант 15МБ5

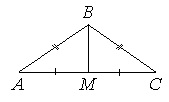
На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.

Алгоритм выполнения

1. Находим ЕС.
2. Определяем значение СD.
3. Из прямоугольного треугольника АСD по т.Пифагора находим ЕD.

Решение:

Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12.

Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12.

Рассмотрим ∆ЕСD. Т.к. АВСD прямоугольник, то угол С=90 0 , и ∆ЕСD прямоугольный.

Тогда по т.Пифагора ЕD 2 =ЕC 2 +СD 2 . Получаем:

Вариант 15МБ6

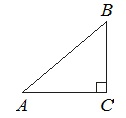
В треугольнике АВС угол С равен 90 0 , АВ=25, АС=24. Найдите cos B.

Алгоритм выполнения

1. По т.Пифагора находим величину катета ВС.
2. По формуле-определению для косинуса находим cos B как отношение прилежащего катета к гипотенузе.

Решение:

Из прямоугольного ∆АВС по теореме Пифагора имеем: АВ 2 =АС 2 +ВС 2 .

Вариант 15МБ7

В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС.

Алгоритм выполнения

1. Из вершины В

Проводимость — способность живой ткани проводить возбуждение.

Решение

В ∆ADB угол А является противолежащим к BD. Поэтому sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15.

Из ∆ADB по т.Пифагора имеем: AB 2 =AD 2 +BD 2 →

Т.к. ∆АВС равнобедренный, то высота BD, проведенная к основанию, является и медианой. Поэтому АС=2АD=2·20=40.

Площадь ∆АВС равна:

Вариант 15МБ8

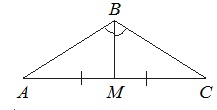
В равнобедренном треугольнике АВС медиана ВМ, проведенная к основанию, равна 12, а tg А=12/5. Найдите длину боковой стороны треугольника АВС.

Алгоритм выполнения

1. Доказываем, что ∆АВМ прямоугольный.
2. Из ∆АВМ, используя формулу-определение для тангенса, находим АМ.
3. Из ∆АВМ по теореме Пифагора находим АВ.

Решение:

Т.к. ∆АВС равнобедренный, то медиана ВМ, проведенная к основанию, является и высотой. Тогда ∆АВМ прямоугольный.

Из ∆АВМ по теореме Пифагора АВ 2 =АМ 2 +ВМ 2 →

Вариант 15МБ9

В треугольнике АВС угол В равен 120 0 . Медиана ВМ делит угол В пополам и равна 27. Найдите длину стороны АВ.

Алгоритм выполнения

1. Определяем величину угла АВМ.
2. Доказываем, что ∆АМВ прямоугольный.
3. Находим АВ, используя формулу-определение для косинуса.

Решение:

По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет

Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ.

В прямоугольного ∆АМВ:

Вариант 15МБ10

В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон.

Алгоритм выполнения

1. Доказываем, что ∆АКВ прямоугольный.
2. Из ∆АКВ по т.Пифагора находим АК.
3. Находим АС как 2АК.
4. Находим МN как среднюю линию.

Решение:

Т.к. ∆АВС равнобедренный, то медиана ВК, опущенная на основание АС, является и высотой. Поэтому угол АКВ равен 90 0 , и ∆АКВ прямоугольный.

Из прямоугольного ∆АКВ по т.Пифагора АВ 2 =АК 2 +ВК 2 .

Поскольку ВК медиана, то АС=2АК=2·24=48.

Линия, соединяющая в треугольники середины двух сторон, называется средней линией. Ее величина составляет половину третьей стороны (которой она параллельна).

Вариант 15МБ11

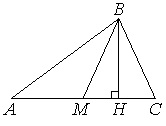
В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН.

Алгоритм выполнения

1. Находим длину отрезков АМ и МС как половину от АС.
2. Доказываем, что ВН является медианой в ∆МВС. Отсюда определяем, что МН – половина от МС.
3. Находим АН как сумму АМ и МН.

Решение:

Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28.

По условию ВС=ВМ, поэтому ∆МВС равнобедренный с основанием МС и равными боковыми сторонами ВМ и ВС. Тогда высота, проведенная к основанию, является еще и медианой. Отсюда следует, что МН=НС=МС/2=28/2=14.

Вариант 15МБ12

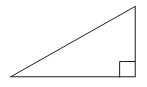
Найдите площадь прямоугольного треугольника, если его гипотенуза равна √17, а один из катетов равен 1.

Алгоритм выполнения

1. Находим величину 2-го (неизвестного) катета по т.Пифагора.
2. Определяем площадь треугольника как полупроизведение катетов.

Решение:

Обозначим 1-й (известный) катет через а, 2-й – через b, гипотенузу – через с.

По т.Пифагора a 2 +b 2 =c 2 . Отсюда:

Т.к. треугольник прямоугольный, то его площадь можно найти по ф-ле: S=a·b/2. Тогда: S=1·4/2=2.

Вариант 15МБ13

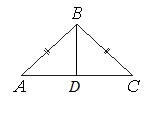
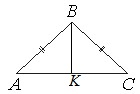
В равнобедренном треугольнике АВС основание АС равно 32, площадь треугольника равна 192. Найдите длину боковой стороны АВ.

Алгоритм выполнения

1. Используя формулу для площади треугольника S=ah/2 и зная величину а (по условию – основание АС), найдем высоту ∆АВС. Отображаем высоту на рисунке, обозначив ее пересечение с основанием буквой К.
2. Доказываем, что высота ВК является и его медианой. Отсюда находим АК.
3. Из ∆АКВ по т.Пифагора находим АВ.

Решение:

Площадь треугольника определяется по ф-ле: S=ah/2, где а=АС=32. Отсюда находим высоту ВК: BK=h=2S/a → ВК=2·192/32=12.

Т.к. ∆АВС равнобедренный, то высота, опущенная в нем на основание, является и медианой. Тогда АК=АС/2=32/2=16.

Из прямоугольного ∆АКВ по т.Пифагора АВ 2 =АК 2 +ВК 2 . Получаем:

🎦 Видео

№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать

№265. В равнобедренном треугольнике ABC с основанием АС проведены биссектриса AF и высота АН.Скачать

№149. Отрезок AD перпендикулярен к плоскости равнобедренного треугольника ABC. Известно,Скачать

№120. В равнобедренном треугольнике ABC с основанием АС проведена медиана BD. На сторонах АВ и СВСкачать

№119. В равнобедренном треугольнике DEK с основанием DK=16см отрезок EF— биссектриса,Скачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

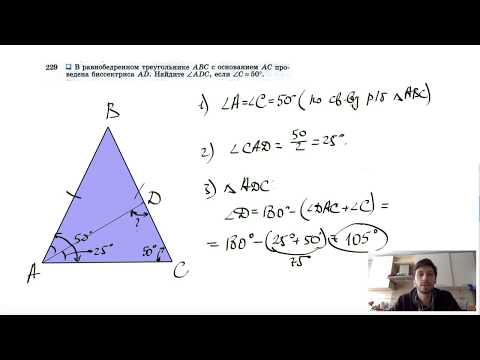
№229. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD.Скачать

№ 109 - Геометрия 7-9 класс АтанасянСкачать

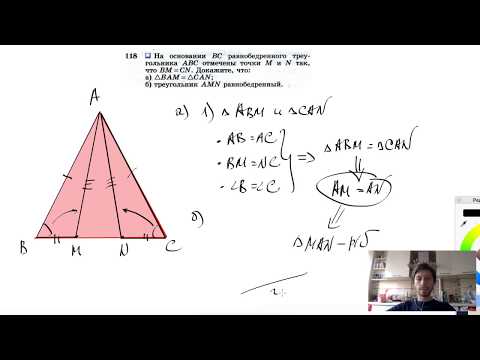
№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать

Геометрия В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BDСкачать

Геометрия, Атанасян, задача 109Скачать

Равнобедренный треугольник. 7 класс.Скачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Задача с решением о нахождении величины угла в равнобедренном треугольникеСкачать

№ 108 - Геометрия 7-9 класс АтанасянСкачать