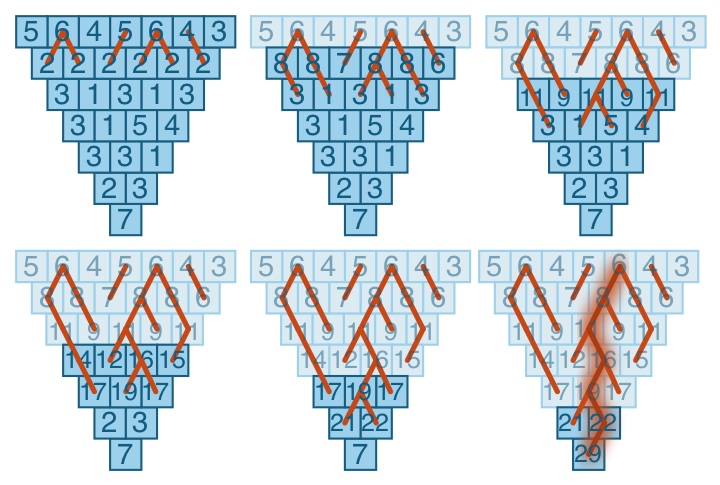Задача о треугольнике чисел (8 видео) | Курс школьной геометрии

Задача о треугольнике чисел

Список секций
Математика
Треугольник Паскаля

Содержание

Треугольник Паскаля
Олимпиадная задача по информатике — Треугольные числа
Золотая пирамида — задача про треугольник, составленный из чисел
Рекурсия
Динамическое программирование
Решения игроков CheckiO
🔥 Видео

Видео:Задача, которую исключили из экзамена в АмерикеСкачать

Треугольник Паскаля

Автор работы награжден дипломом победителя III степени

Замечательная геометрическая фигура и самая популярная в школьной программе геометрии — это треугольник. Но треугольники «поселились» не только на страницах учебника геометрии. В данной работе мы рассмотрим не обычный треугольник, а треугольник, состоящий из чисел – треугольник Паскаля, его свойства, связь с числами Фибоначчи и биномиальными коэффициентами.

Познакомиться с таким математическим объектом, как треугольник Паскаля

Пополнить запас научных знаний.

Продолжить знакомство с основными историческими этапами возникновения и развития математической науки, судьбами открытий, именами людей, творивших науку. В первую очередь с биографией ученого Блеза Паскаля.

Самостоятельно попытаться составить данный треугольник.

Рассмотреть свойства треугольника Паскаля.

Определить значимость открытия треугольника Паскаля.

Сформулировать вывод и итоги исследования.

Треугольник Паскаля обладает рядом замечательных свойств, поэтому и носит имя одного из выдающихся людей.

Актуальность данной работы не вызывает сомнения, поскольку обусловлена, с одной стороны большим интересом к теме «Треугольник Паскаля» в современной науке, с другой стороны, её недостаточной разработанностью.

Навыки решения задач с применением треугольника Паскаля помогут в рамках изучения школьного курса математики, при решении олимпиадных задач.

Сбор первоначальных сведений о треугольнике в энциклопедической и учебно-научной литературе.

Построение треугольник Паскаля.

Выявление «волшебных» свойств чисел треугольника.

Изучение возможностей применения треугольника Паскаля.

Формулирование итогов и выводов.

аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;

поиск информации в интернет — ресурсах.

1.Биография Блеза Паскаля

Прогресс человечества во многом связан с открытиями, сделанными гениями.

Одним из них является Блез Паскаль — французский математик, физик, философ и мастер прозы.

Родился Блез Паскаль в 1623 г. 19 июня в Клермон — Ферране, в семье председателя суда города Этьена Паскаля.

Род Паскалей отличали незаурядные способности, а Блеза одаренность посетила с раннего детства. Этьен Паскаль уделил много внимания развитию умственных способностей сына и уже в 16 лет Блез сочинил труд под названием «Опыт о конических сечениях» в котором содержалась теорема известная, как теорема Паскаля.

Вклад Паскаля в науках очень велик. Вот лишь некоторые из них: заложил основы современной теории вероятностей и математического анализа, сформулировал основной закон гидростатики, написал множество трудов по философии, изобрел шприц, создал гидравлический пресс и вычислительное устройство «Паскалин» (прототип калькулятора), изобрел тачку, придумал омнибус — конные экипажи с фиксированными маршрутами, ставшие впоследствии первым видом регулярного общественного транспорта и пр.

Умер Блез Паскаль 19 августа 1662 года.

Вследствие его больших вкладов в изучение давления в физике, в честь Паскаля назвали единицу измерения давления (Па). Так же в честь Паскаля назвали язык программирования Pascal .

2.Определение и основные свойства треугольника Паскаля.

2.1 История треугольника.

Треугольник Паскаля был известен задолго до 1653 года — даты выхода «Трактата об арифметическом треугольнике» Блеза Паскаля

Похожий треугольник представлен в качестве иллюстрации в книге китайского математика Яна Хуэя, изданной в 1303 году.

О его свойствах было известно также и замечательному персидскому поэту и философу Омару Хайяму еще в начале 12 века. Причем считается, что он познакомился с ним из трактатов арабских и индийских ученых, написанных ранее.

2.2 Построение треугольника Паскаля.

«Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике» (Мартин Гарднер).

Треугольником Паскаля называется бесконечная треугольная таблица, в которой (рис.1):

на вершине и по боковым сторонам стоят единицы,

-каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строке.

Если очертить треугольник Паскаля, то получится равнобедренный треугольник. Продолжать треугольник можно бесконечно.

2.3 Основные свойства треугольника Паскаля.

Для любой строки под номером n (n = 0, 1, 2…) верно:

Первое и последнее числа – 1; второе и предпоследнее – n.

Строки треугольника симметричны относительно вертикальной оси треугольника.

Сумма чисел n-й строки треугольника Паскаля равна (рис.2)

Первая диагональ — это натуральные числа, идущие по порядку (рис.3).

Вторая диагональ — это «треугольные» числа (Рис.3). Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника — как классический пример начальная расстановка шаров в бильярде.

Третья диагональ — это «пирамидальные» числа (один шар мы можем положить на три — итого четыре, под три подложим шесть — итого десять, и так далее) (рис.4).

Четвертая диагональ – это «фигурные числа» в четырехмерном измерении. Это можно представить только в виртуальном мире. Один шар касается четырех, а те, в свою очередь, десяти…

Каждое число треугольника Паскаля равно сумме чисел предыдущей диагонали, стоящей над этим числом.

В каждой строке сумма чисел на нечётных местах равна сумме чисел на чётных местах.

Если номер строки – простое число, то все числа этой строки, кроме 1, делятся на это число.

Каждое число, уменьшенное на 1, равно сумме всех чисел, заполняющих параллелограмм, ограниченный правыми и левыми диагоналями, на пересечении которых стоит это число.

Бином Ньютона – возведение выражения (a + b) в степень. При возведении в степень получаются коэффициенты, равные числам в треугольнике Паскаля.

Сумма чисел n-й восходящей диагонали, проведенной через строку треугольника с номером n − 1, есть n-е число Фибоначчи (число равно сумме двух предыдущих чисел) (рис.5).

Если нечётное число в треугольнике Паскаля заменить на точки контрастного цвета, а чётные — белого цвета, то треугольник Паскаля разобьётся на более мелкие треугольники, образующие изящный узор. Удивительное свойство треугольника Паскаля.

3. Применение треугольника Паскаля.

Где же применяется треугольник Паскаля?

При решении комбинаторных задач.

Треугольник Паскаля используется для решения различных задач в области физики:

принцип минимума потенциальной энергии;

материальные точки и центр тяжести;

центр тяжести системы двух материальных точек;

центр тяжести стержня с многими грузами;

невозможность вечного двигателя.

С появлением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении основ программирования.

Вот далеко не полный перечень свойств чисел треугольника Паскаля и его многочисленных применений.

4. Применение свойств треугольника Паскаля в решении математических задач.

Свойства треугольника Паскаля, наверное, были бы не столь значимы, если бы на их основе нельзя было решать математические задачи. Такие задачи можно встреть в ОГЭ, ЕГЭ и в олимпиадных задачах старшего школьного уровня. Треугольник Паскаля используется при решении комбинаторных задач, для решения различных задач в области физики. С построением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении программирования.

Найдите сумму первых 8 треугольных чисел.

Найдем сумму первых восьми чисел 3 диагонали треугольника Паскаля. (рис.6) Получится 120.

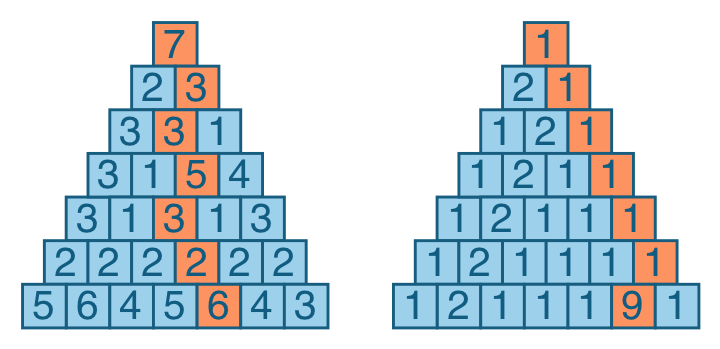
Вася построил из шариков пирамиду. Известно, что на её строительство ушло 286 шариков, сколько «этажей» в Васиной пирамиде?

В данной задаче нам известно, что на строительство пирамиды ушло 286 шариков. Найдем решение с помощью треугольника Паскаля, в котором количество прямоугольников, пересеченных зеленой линией, будет наш ответ. (рис. 7)

Ответ: 11 «этажей».

В магазине «Теплица» продается 6 различных сортов помидор. Сколькими способами можно выбрать из них 3 сорта помидор?

В данной задаче нам даны различные сорта, поэтому повторений не будет и порядок выбора сортов нам неважен, нам важно количество, а именно 3. Найдем решение с помощью нашего треугольника Паскаля, в котором пересечении 3-й диагонали и 6 строки будет наш ответ (рис.8).

На плоскости даны 11 точек, из которых никакие три не лежат на одной прямой и никакие четыре не лежат на одной окружности. Сколько существует окружностей, каждая из которых проходит через три данные точки

Ответ находится на пересечении 11 ряда и 3 диагонали: Это число – 165 (рис.9).

Ответ: 165 окружностей.

Танк может двигаться по квадратам, видимым на карте, размером 4 на 4 только вправо или вниз. Он стоит в точке А. Из штаба пришло задание прибыть в точку В. Сколько маршрутов передвижения может использовать экипаж?

В квадраты a2, a3, a4, а1, b1, c1, d1 танк попадёт 1 способом, в квадрат b2 может добраться 2 способами (рис.10(а)). В квадрат с2 и b3 — 3 способами, d2 и b4 — 4 способами, в c3 – 6 способами, d3, c4 – 10 способами и в квадрат d4 (точка В) – 20 способами. (рис.10(б))

Ответ: 20 способов.

Решив задачу, мы замечаем, что полученные на «карте» числа образуют треугольник Паскаля. Таким образом, можно сделать вывод, что число в треугольнике Паскаля показывает количество способов передвижения от вершины треугольника до данного числа.

Из пункта А по сети дорог идет группа из человек. На каждом перекрестке, начиная с А, пришедшие туда люди делятся пополам – половина идет по направлению l, половина – по направлению m (рис.11). Сколько человек придет в пункты В, С, D, …, I соответственно?

Количество людей, пришедших в искомые точки соответствует числам n-ой строки. В данном случае, n = 7, следовательно¸ искомое количество людей на каждом перекрестке соответствует 7 строке треугольника Паскаля (рис.12).

Ответ: 1, 7, 21, 35, 35, 21, 7, 1.

Возведите в степень: (u — v) 5

У нас есть (a + b) n , где a = u, b = -v, и n = 5. Мы используем 5-й ряд треугольника Паскаля:

Тогда у нас есть:

( u — v ) 5 = ( u + (- v )) 5 = 1( u ) 5 + 5( u ) 4 (- v ) 1 + 10( u ) 3 (- v ) 2 + 10( u ) 2 (- v ) 3 + 5( u ) (- v ) 4 +1(- v ) 5 = u 5 — 5 u 4 v + 10 u 3 v 2 — 10 u 2 v 3 + 5 uv 4 — v 5 .

В ходе исследования мы убедились, что треугольник Паскаля, несмотря на кажущуюся простоту, действительно обладает рядом замечательных свойств, знание которых будет полезно. Этот треугольник широко используется в математике для решения различных видов задач. Треугольник Паскаля имеет применение не только в математике, но и в физике, информатике.

Изучение темы «Треугольник Паскаля» оказалось очень интересной и необычной. Работа над проектом показала, что математика – это не только точная, но и красивая наука.

Гиндикин, С.Г. Рассказы о физиках и математиках/ С.Г.Гиндикин. – М.: Терра, 2013. – 480с.

Энциклопедия для детей Аванта+: В 57 т. Т. 11. Математика/ под ред. М. Аксёновой, В. Володина, М. Самсоновф – М.: Аванта+, 2003. — 688 с.

Корбалан, Ф. Мир математики: В 40 т. Т.1. Золотое сечение, математический язык красоты/ Пер. с исп. — М.: DeAgostini, 2014. — 164 с.: ил.

Гарднер, М. Математические новеллы. (Mathematics Games) / Пер. с англ. Ю.А.Данилова; под ред. Я.А. Смородинского — М.: Мир, 1974. — 456 с.

Успенский, В.А. Треугольник Паскаля. Популярные лекции по математике. Выпуск 43/ ред. В.В. Донченко — 2-е изд. доп. — М.: Наука, 1979. — 48 с.: ил.

Видео:Треугольник ПаскаляСкачать

Олимпиадная задача по информатике — Треугольные числа

Здравствуйте! Сегодня разберём олимпиадную задачу по информатике, которая называется треугольные числа.

Задача треугольные числа.

Школьник Никита этим летом отдыхал со своими родителями. Его любимым занятием на пляже было складывать из камешков правильные треугольники (правильным называется треугольник, у которого все стороны равны). Никита и не предполагал, что числа, из которых можно сложить правильный треугольник, называются треугольными. Вот несколько треугольных чисел: 1, 3, 6, 10, … .

Помогите Никите по заданному количеству камешков N найти наибольшую сторону правильного треугольника, который из них можно сложить. Например, если у Никиты 30 камешков, то длина наибольшей стороны правильного треугольника, который из них можно сложить, будет 7.

Тесты для самопроверки:

30	7
29	7
28	7
27	6
9876543210000	4444443
9223372036854775807	4294967295

Рассмотрим треугольные числа. Видим, что первое треугольное число — это просто 1. Второе число — это сумма чисел до 2 (1+2), третье число — сумма чисел до 3 (1+2+3) и т.д.

Плюс ко всему, второе число образует треугольник со стороной 2, третье число со стороной 3 и т.д.

Рассмотрим треугольное число по номером n. Видим, что это сумма арифметической прогрессии.

Свернём по формуле арифметической прогрессии. Число Sn (сумма арифметической прогрессии) в нашей задаче это количество камней, которое вводит пользователь. Число n в данном уравнении обозначает порядковый номер треугольного числа или длину стороны правильного треугольника, который можно составить из данного количества камней.

Остаётся решить данное уравнение относительно n в целых числах, чтобы разгадать нашу задачу.

Последние уравнение это и есть ответ в нашей задаче. Если n — будет дробным, значит мы должны его округлить в меньшую сторону, т.к. наше уравнение решается только в целых числах. (Дробное количество камней не может быть).

Запрограммируем данную задачу на C#

Т.к. число 9223372036854775807 * 8 превышает максимальное число даже для типа ulong, то будем использовать специальный тип BigInteger.

Для того, чтобы использовать BigInteger, нужно в ссылках добавить System.Numerics . И прописать using System.Numerics в программе.

Для этого типа данных не работает стандартная функция извлечения корня Math.Sqrt(), поэтому мы напишем свою функцию извлечения корня основанную на методе Ньютона. Эта функция извлекает корень и округляет результат в меньшую сторону. Об этом методе можете прочитать подробно в статье на этом сайте.

На этом всё, до свидания!

Видео:Задача про соотношение сторон. Геометрия 7 класс.Скачать

Золотая пирамида — задача про треугольник, составленный из чисел

В этом выпуске рассмотрим классическую задачу, известную под названием «Золотая гора». На CheckiO её реализовали в этой задаче.

Представьте себе треугольник, составленный из чисел. Одно число расположено в вершине. Ниже размещено два числа, затем три, и так до нижней грани. Вы начинаете на вершине, и нужно спуститься к основанию треугольника. За каждый ход вы можете спуститься на один уровень и выбрать между двумя числами под текущей позицией. По ходу движения вы «собираете» и суммируете числа, которые проходите. Ваша цель — найти максимальную сумму, которую можно получить из различных маршрутов.

Рассмотрим различные методы решения.

Рекурсия

Первым делом в голову приходит мысль использовать рекурсию и просчитать все пути от вершины. Когда мы спускаемся на один уровень, то все доступные числа ниже образуют новый меньший треугольник, и можно запустить нашу функцию уже для нового подмножества и так пока не достигнем основания.

Как мы видим, на первом уровне мы запустим нашу функцию два раза, затем 4, 8, 16 раз и так далее. В итоге мы получим сложность алгоритма 2 N и, например, для 100-уровневой пирамиды нам нужно будет уже где-то ≈10 30 вызовов функции. Многовато.

Динамическое программирование

Что если попробовать использовать принцип динамического программирования и разбить нашу проблему на множество мелких подзадач, результаты которых мы затем аккумулируем. Попробуйте взглянуть на треугольник вверх ногами. А теперь на второй уровень (то есть предпоследний от основания). Для каждой ячейки мы можем решить, каким будет лучший выбор в наших маленьких трёхэлементных треугольничках. Выбираем лучший, суммируем с рассматриваемой ячейкой и записываем результат. Таким образом, мы получили наш треугольник, но на один уровень ниже. Повторяем данную операцию снова и снова. В результате нам нужно (N-1)+(N-2)+…2+1 операций и сложность алгоритма равна N 2 .

Решения игроков CheckiO

Пользователь gyahun_dash написал интересную реализацию описанного выше метода ДП в своем решении «DP». Он использовал reduce, чтобы проходить по парам строк, и map чтобы обработать каждую из них.

Игрок evoynov использовал двоичные числа, чтобы перебрать все возможные маршруты, представленные как последовательность 1 и 0 в своем решении «Binaries». И это наглядный пример сложности алгоритма с рекурсией и перебором всех маршрутов.

И чтобы не было скучно, посмотрим на легкий мозгодробитель от пользователя nickie и его однострочник «Functional DP», который только формально состоит из двух строк. Конечно, это решение из категории «Творческих» («Creative»). Не думаю, что автор использует такое на боевом коде. А просто для так для веселья, почему бы и нет.

Вот и всё на сегодня. Делитесь вашими идеями и мыслями.

Спасибо CheckiO за интересную задачу.