Видео:Равнодействующая и сложение силСкачать

ЧТО ТАКОЕ ВЕКТОР СИЛЫ

При сооружении и проектировании мостов, зданий, кранов, машин инженеров очень заботит сложение сил или же разность сил для определения силы, необходимой для достижения равновесия. Можно показать, что силы — это векторы, т. е. они подчиняются правилу геометрического сложения.
Векторному сложению и разложению уравновешенных сил посвящен раздел физики, называемый «статикой». Это большой, но скучный раздел физики, и большинство учебников уделяет ему много места, излагая приемы решения задач инженерной статики. Мы ограничимся лишь несколькими примерами, и даже их, пожалуй, лучше было бы опустить, чтобы уделить больше времени изучению силы и движения.
Прежде всего мы должны удостовериться в том, что силы — это векторы. Сказать, что они должны быть векторами, поскольку они характеризуются величиной и направлением, недостаточно. Это не убеждает нас в том, что силы складываются геометрически.
Хотя это утверждение кажется вполне правдоподобным, особенно тем, кто имеет дело с канатами и веревками на кораблях или кому приходится заниматься разбивкой палаток, мы же должны проворить его непосредственно.
Опыт по определению вектора силы

Она равна и проти воположна силе FС. Это требует дополнительного доказательства, поскольку FС не равнодействующая (сумма) двух других сил, а «равновесная» сила, необходимая, чтобы им противостоять.
Рис. Косвенная проверка векторного сложения сил.
Равновесие сил

В этом случае мы говорим, что силы находятся «в равновесии». Если сумма нескольких сил равна нулю, то это должно быть видно на диаграмме векторного сложения; длина линии, соединяющей исходную точку диаграммы с конечной, должна быть равна нулю. Это означает, что векторная диаграмма должна представлять собой замкнутую фигуру.
Таким образом, если сумма сил равна нулю, то конец векторного многоугольника должен прийти обратно к началу. Это иллюстрирует рис. 3. Условие равенства нулю равнодействующей для постоянного равновесия сил должно выполняться для всей конструкции, например для всего крана или моста, но оно должно также выполняться для каждой отдельной детали конструкции, находящейся в состоянии равновесия.
Применяя это условие к какой-нибудь определенной детали, например к стреле крана, к одной опоре моста, к заклепке, связывающей воедино несколько различных деталей моста, или к грузу маятника, нужно быть внимательным и учитывать все силы, действующие на данную деталь. Тогда мы сможем утверждать, что имеем полный набор сил, образующих замкнутую векторную диаграмму, если, конечно, деталь находится в равновесии.
При решении задач не следует включать в рассмотрение силы, приложенные к другим деталям. Сначала выберите и пометьте выбранную деталь, которая, как вы считаете, находится в равновесии.
Равновесие трех сил, треугольник сил

а — три силы в равновесии) б — три силы не находятся в равновесии.
Этим пользуются при решении инженерных задач. Во многих конструкциях на каждую деталь, играющую важную роль, действуют как раз три силы. Чтобы конструкция была устойчивей, каждая деталь должна оставаться в состоянии покоя; сумма всех действующих на нее сил должна быть равна нулю. Таким образом, если к любой детали приложены три силы, мы строим для них замкнутый треугольник.
Похожие страницы:
Понравилась статья поделись ей
Leave a Comment
Для отправки комментария вам необходимо авторизоваться.
Видео:Силы взаимодействия молекул. 10 класс.Скачать

Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Видео:Урок 13 (осн). Взаимодействие молекул. Смачивание и несмачиваниеСкачать

Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Видео:Урок 23 (осн). Инерция. Взаимодействие тел. ИнертностьСкачать

Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .
Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
Видео:Взаимодействие тел. Масса тела. Единицы массы | Физика 7 класс #14 | ИнфоурокСкачать

Взаимодействие трех и более зарядов
Читатель: Предположим, что три заряда (+q, +q и +q) расположены на одной прямой (рис. 2.1) Расстояние между соседними зарядами равно а. Можно ли утверждать, что заряд 1 действует на заряд 3 с силой, определяемой законом Кулона 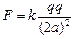
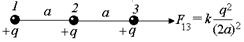
Автор: Экспериментально установлено, что сила взаимодействия двух зарядов не изменяется, если вблизи них поместить еще какие-либо заряды.
Пусть имеются заряд q и заряды q1, q2, q3,…, qN. Тогда результирующая сила 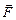
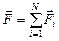
где 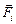
Задача 2.1. На одной прямой находятся заряды (–2q), +2q и +q. Расстояние между соседними зарядами а. Найти величину результирующей силы, действующей на заряд +q.
| (–2q), +2q, +q а | Решение. Введем ось х (рис. 2.2). 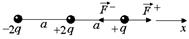 Рис. 2.2 Рис. 2.2 |
| 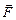 | = ? | = ? |
Согласно формуле (2.1) результирующая сила 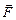
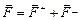
В проекции на ось х
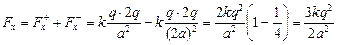
Так как 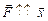
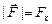
Ответ: 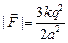
СТОП! Решите самостоятельно: В1–В3, С1.
Задача 2.2. Два положительных заряда q и 2q закреплены неподвижно на расстоянии а друг от друга. На каком расстоянии от заряда q следует разместить заряд Q, чтобы он находился в положении равновесия?
| q 2q Q a | Решение. Введем ось х (рис. 2.3). Рис. 2.3 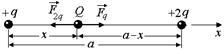 Запишем условие равновесия для заряда Q в проекции на ось х: Запишем условие равновесия для заряда Q в проекции на ось х: |
| x = ? |
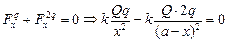
Решим это уравнение относительно х:
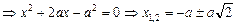
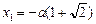
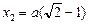
Отрицательный корень мы отбрасываем: если заряд Q окажется левее заряда q, то в положении равновесия он находиться не сможет.
Ответ: 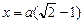
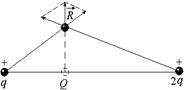 Рис. 2.4 Рис. 2.4 | Читатель: Устойчиво ли это равновесие? Автор: Вообще говоря, нет. Если сместить заряд Q чуть-чуть перпендикулярно оси х, возникнут силы, удаляющие его от положения равновесия (рис. 2.4). |
Читатель: А если заряду Q разрешить двигаться только вдоль оси х (например, посадив все заряды на гладкую проволоку)?
Автор: Тогда положение равновесия устойчиво. Допустим, мы сместились из положения равновесия вправо в точку 1 (рис. 2.5). Тогда сила вдоль оси х (со стороны заряда +q) уменьшилась, а сила против оси х (со стороны заряда +2q) возросла. Значит, равнодействующая будет направлена против оси х, и заряд Q вернется в положение равновесия. То же будет при попытке сместить заряд влево от положения равновесия в точку 2.
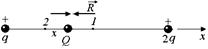
СТОП! Решите самостоятельно: В4, В5, С2.
Задача 2.3. Два положительных заряда +q находятся на расстоянии а друг от друга. Найти результирующую силу, с которой они действуют на такой же заряд +q, равноудаленный на расстояние а от каждого заряда.
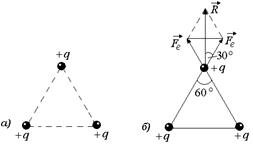 Рис. 2.6 Рис. 2.6 |
| q a |
| R = ? |
Решение. Все заряды находятся в вершинах правильного треугольника (рис. 2.6,а). Из симметрии задачи легко видеть, что результирующая сила направлена вертикально вверх (рис. 2.6,б), причем ее модуль равен 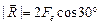
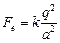
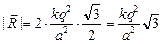
Ответ: 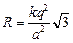
СТОП! Решите самостоятельно: В8, В9, С7.
Задача 2.4. В четырех вершинах квадрата находятся одинаковые заряды q > 0. Какой заряд надо поместить в центр, чтобы система находилась в положении равновесия?
| q | Решение. Ясно, что заряд в центре системы должен быть отрицательным (рис. 2.7,а). Из симметрии задачи очевидно, что при любых значениях q заряд Q всегда будет в равновесии, а вот заряд q – не всегда. |
| Q = ? | |
Запишем условие равновесия для одного из зарядов q: 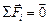 . Пусть сторона квадрата равна а (рис. 2.7,б). Тогда диагональ квадрата равна . Пусть сторона квадрата равна а (рис. 2.7,б). Тогда диагональ квадрата равна 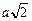 , половина диагонали , половина диагонали 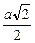 . Введем ось х вдоль диагонали и запишем 2-й закон Ньютона в проекции на эту ось: . Введем ось х вдоль диагонали и запишем 2-й закон Ньютона в проекции на эту ось: 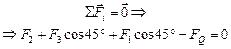 . (1) Здесь . (1) Здесь 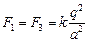 ; ; 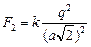 ; ; 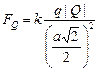 . . | 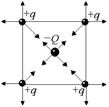 а а 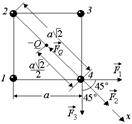 б Рис. 2.7 б Рис. 2.7 |
Подставим эти значения в формулу (1):
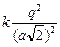
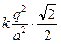
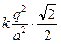
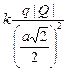
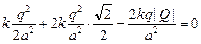
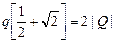
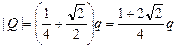
Дата добавления: 2016-04-11 ; просмотров: 8352 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
📺 Видео
Обменное взаимодействие: тайная сила, определяющая облик ВселеннойСкачать

Урок 25 (осн). Задачи на взаимодействие телСкачать

Силы в механике. 9 класс.Скачать

Броуновское движение. Силы взаимодействия молекул | Физика 10 класс #26 | ИнфоурокСкачать

Урок 51. Первый закон Ньютона. Взаимодействие тел и их ускорение.Скачать

Слабое взаимодействие | 4 фундаментальных взаимодействияСкачать

Закон КулонаСкачать

Фундаментальные взаимодействия: четыре силы, приводящие в движение Вселенную!Скачать

Урок 32 (осн). Сила. Единицы силы. Изображение силСкачать

Урок 118. Потенциальная энергия гравитационного взаимодействия. Вторая космическая скоростьСкачать

Сильное взаимодействие | 4 фундаментальных взаимодействияСкачать

Силы Ван-дер-Ваальса (видео 1) | Силы межмолекулярного взаимодействия | ХимияСкачать

Вводный урок по теме: «Взаимодействие тел». Видеоурок по физике 7 классСкачать

Урок 140. Опыт Перрена. Масса молекул. Взаимодействие молекулСкачать