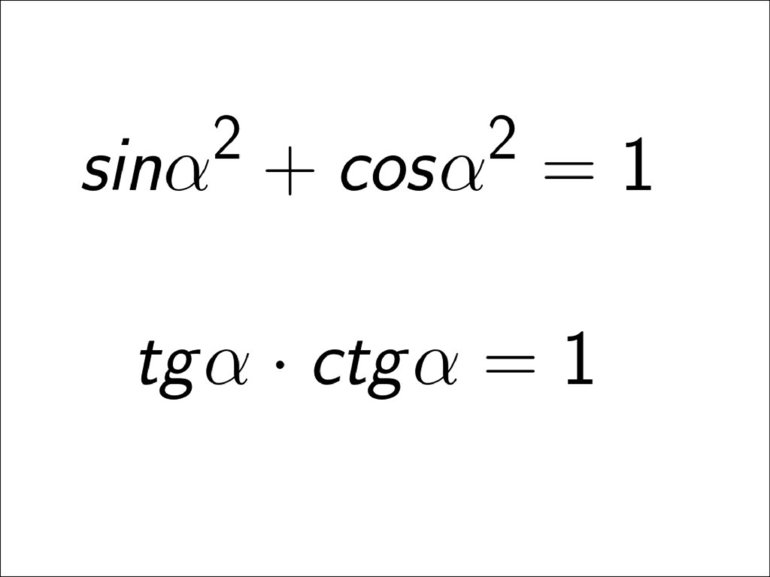Высота прямоугольного треугольника является синусом

Видео:8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

Общие сведения

Следует отметить, что в геометрии существуют элементы, используя которые можно строить простые и сложные фигуры. Простейшим из них считается точка. С ее помощью можно создать прямую, луч, отрезок и угол. Точкой называется базовый «кирпич» геометрии, позволяющий осуществлять построение других элементов математической науки.

Прямая — совокупность множества точек, лежащих в одной плоскости и соединенных между собой таким образом, чтобы образовалась некоторая линия без перегибов и переломов. У нее нет вообще границ. Если говорят, что нужно провести прямую, то чертится только ее часть, а затем обозначается произвольной строчной буквой (a, b, c и т. д.). Простейшая фигура не имеет начала и конца. Математически границы записываются следующим образом: (- ∞; ∞). Следовательно, левая граница находится в точке — ∞, а правая — ∞.

Луч — разновидность прямой линии, имеющей только одну границу (точку). Из последней исходит прямая в бесконечность. Примером этой модели является Солнце, испускающее пучки световой энергии. Оно является источником света, который может проходить не только через Солнечную систему, но и уходить за ее пределы в бесконечность (космическое пространство). Луч обозначается также строчной литерой. Однако точку-источник следует обозначать прописной буквой.

Отрезком является часть прямой или луча, имеющая некоторые ограничения. Они обозначаются прописными литерами. Моделями являются следующие объекты и процессы: луч Солнца, идущий к Земле (Солнце — Земля), линейка, карандаш и т. д.

Плоским углом называется элементарная фигура, состоящая из общей точки и двух лучей, исходящих из нее и не лежащих на одной прямой. Измеряется в градусах и радианах. Далее следует разобрать виды прямоугольных треугольников.

Видео:Высота в прямоугольном треугольнике. 8 класс.Скачать

Прямоугольный треугольник

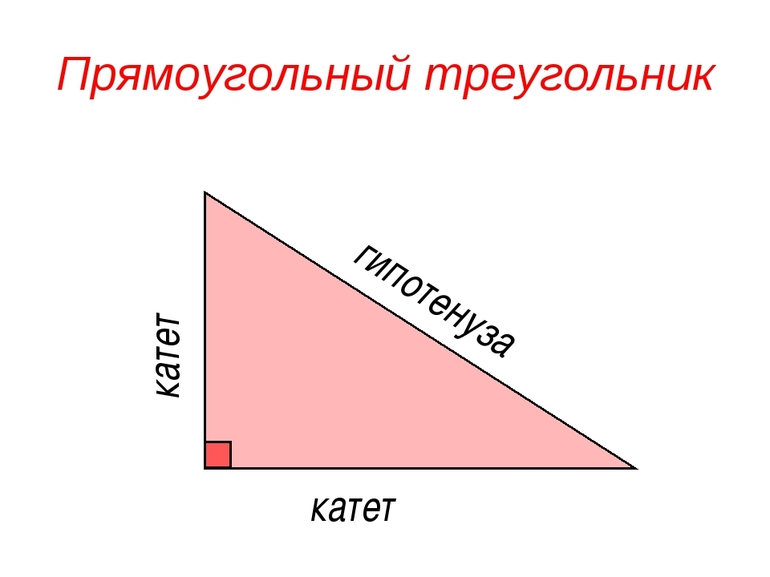
Прямоугольным называется треугольник, имеющий угол, градусная мера которого эквивалентна 90. Он состоит из трех сторон, вершин и углов. К дополнительным параметрам можно отнести следующие:

Стороны, образующие прямой угол, называются катетами. Третья сторона, соединяющая их, является гипотенузой. Все остальные углы являются острыми. Если сумма углов любого треугольника эквивалентна 180 градусам, то 180 — 90 = 90. Следовательно, сумма двух остальных углов составляет 90, а значит, они являются острыми.

Периметр — вспомогательная величина, характеризующая суммарное значение сторон фигуры. Существует также понятие полупериметра. Последним называется полусумма всех его сторон. Площадью называется характеристика треугольника, показывающая его размерность.

Высота в прямоугольном треугольнике, проведенная к гипотенузе — отрезок, опущенный перпендикулярно относительно этой стороны. Ее еще называют проекцией. Медиана — отрезок, соединяющий вершину с серединой стороны. Если она проведена из прямого угла, то эквивалентна половине гипотенузы. Биссектрисой является некоторая прямая, которая делит искомый угол на два равных значения.

Следует отметить, что этот тип треугольника бывает двух видов — разносторонний и равнобедренный. В последнем три последних параметра не совпадают (медиана, высота и биссектриса).

Следует рассмотреть свойства высоты в прямоугольном треугольнике равнобедренного типа. Она является медианой и биссектрисой. Далее следует обратить внимание на теорему, которая применяется для взаимосвязи сторон фигуры.

Теорема Пифагора

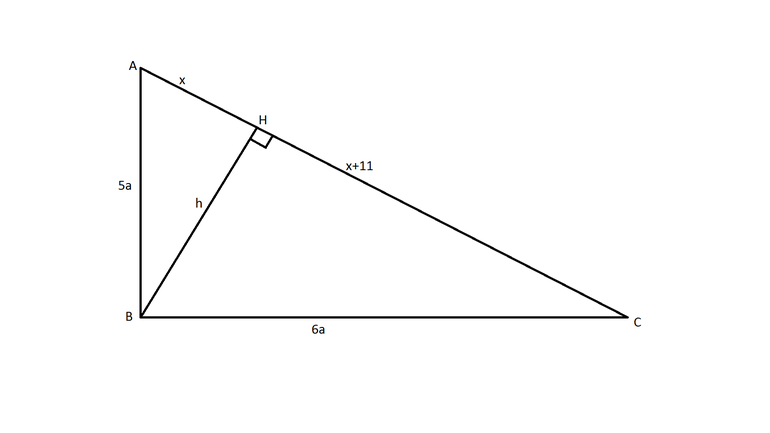
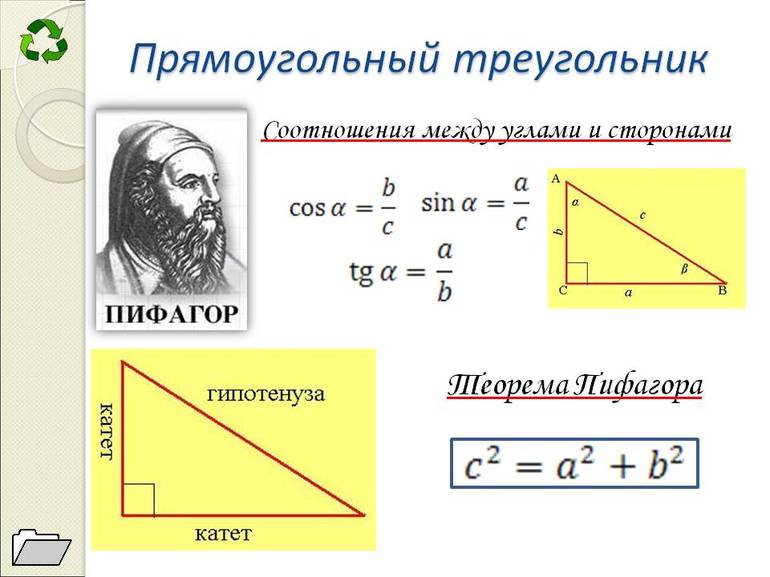
Для удобства треугольник следует обозначить символом «Δ». Связь между сторонами прямоугольного Δ была открыта древнегреческим ученым Пифагором. Утверждение имеет следующую формулировку: в произвольном прямоугольном Δ (со сторонами a, b и c) должно выполняться равенство между квадратом гипотенузы c и алгебраической суммой квадратов двух катетов a и b. Следует отметить, что при несоблюдении этого условия заданная фигура не содержит прямой угол. Математическая запись теоремы имеет такой вид: a^2 + b^2 = c^2.

Доказательств теоремы существует огромное количество, поскольку применяются различные подходы. Однако наибольшей популярностью пользуется способ, полученный из аксиом. Кроме того, дополнительно применяется алгебраическая методика. Для выполнения операции по доказательству соотношения a^2 + b^2 = c^2 необходимо построить прямоугольный Δ с такими сторонами: BC = a, AC = b и AB = c. После этого проводится высота к гипотенузе из вершины, которая является точкой пересечения двух катетов.

В результате образовались два равных угла ∠АНС и ∠ВНС. Кроме того, они являются прямыми по свойству высоты. Затем нужно рассмотреть Δ АВС и Δ АСН (Δ СВН), которые подобны по двум углам. На основании признака подобия можно вывести такие соотношения в виде пропорций:

Далее нужно перемножить крайние и средние члены двух формул: а 2 = c * НВ и b 2 = c * AH. После этого для окончательного доказательства утверждения необходимо только сложить части. Получается равенство такого вида: а^2 + b 2 = c * [НВ + AH] = c 2 .

Утверждение о высоте

Для прямоугольного Δ и высоты была выведена специальная теорема, позволяющая оптимизировать процесс вычисления основных его параметров. Ее формулировка имеет следующий вид: в прямоугольном ΔABC высота CE, опущенная на гипотенузу, делит ее по соотношению квадратов катетов к частям гипотенузы. Для доказательства нужно использовать такой алгоритм:

• Построить ΔABC (∠C = 90).
• Провести высоту к CE к гипотенузе AB.
• Следует доказать соотношение BE / EA = (BC^2) / (AC^2).
• Используя теорему о пропорциональности отрезков прямоугольного Δ, можно сделать вывод о подобии ΔABC и ΔACE.
• На основании 4 пункта получается формула: CA / AB = EA / CA.
• Перемножив крайние и средние члены по свойству пропорции, можно вывести CA^2 = AB * EA.
• Нужно рассмотреть ΔABC и ΔBCE. Их подобие доказывается аналогично пункту 4.
• Пропорция имеет такой вид: BC / AB = BE / BC. Окончательно: BC^2 = AB * BE.
• Разделить полученные равенства в 8 и 6 пунктах на AC^2. Формулу можно править таким образом: BC^2 / AC^2 = BE / EA.

​Теорема доказана. Существуют и другие утверждения о высоте в прямоугольном Δ. Их необходимо также рассмотреть, но без доказательств.

Тригонометрические функции

Полезными при решении различных задач считаются тригонометрические функции. Их всего четыре:

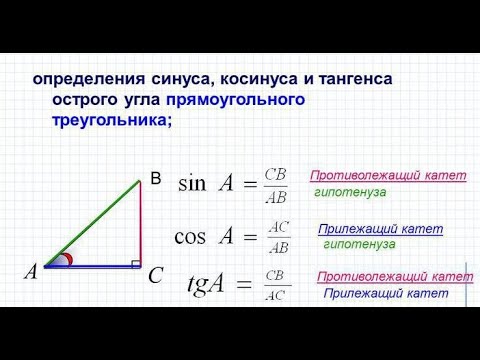
• Синус (sin) эквивалентен отношению противолежащего катета к гипотенузе Δ: sin (∠CBA) = a / c.
• Косинусом (cos) искомого угла называется величина, характеризующая отношение противолежащего катета к гипотенузе: cos (∠CBA) = b / c.
• Тангенс (tg) — это значение отношения двух катетов (противолежащего к прилежащему): tg (∠CBA) = a / b.
• Котангенс (ctg) является обратной величиной для функции tg (∠CBA). Он характеризует отношение прилежащего к противолежащему. Записывается в математическом виде следующим образом: ctg (∠CBA) = b / a или ctg (∠CBA) = 1 / (tg (∠CBA)= 1 / (a / b) = b / a.

Математики выделяют 4 обратные тригонометрические функции: arcsin, arccos, arctg и arcctg. Применяются они, когда получено одно из значений тригонометрической функции. На основании этого можно найти градусную меру угла. Расчет выполняется с использованием специальных таблиц (Брадиса) или при помощи онлайн-калькуляторов.

Другие соотношения

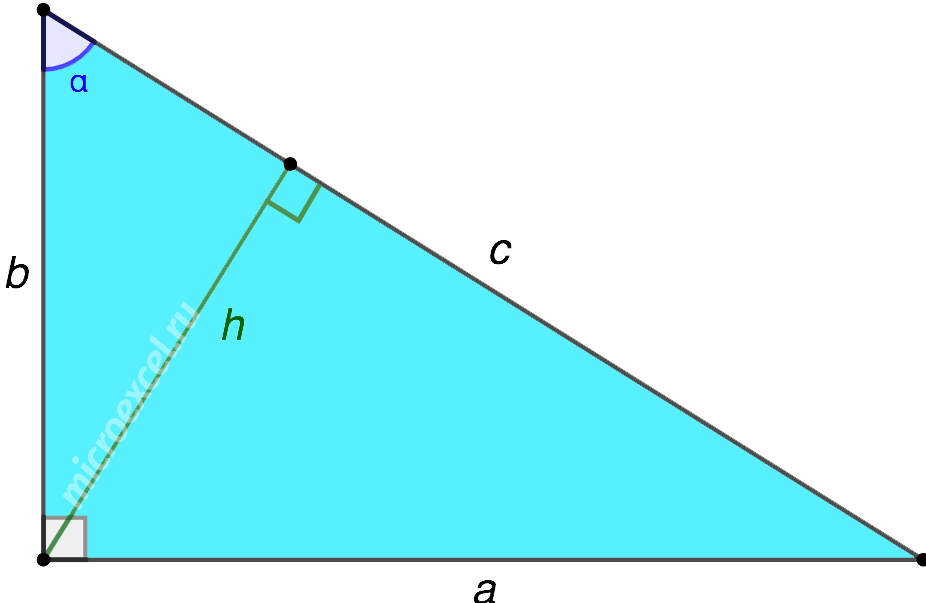
Формулы для нахождения длины высоты происходят от некоторых теорем. Их необходимо знать, поскольку это позволит существенно сэкономить время и избежать множества ошибок при вычислениях. Для этих целей необходимо начертить прямоугольный ΔABC, у которого ∠BAD = 90, а больший катет эквивалентен величине а. Основные теоремы о высоте, проведенной из прямого угла, имеют такие формулировки:

• Высота делит гипотенузу на проекции катетов: Ca = a^2 / c и Cb = b^2 / c.
• Высота эквивалентна средней геометрической величине проекций катетов: h = [Сa * Cb]^(1/2).
• Проведенная из угла 90 высота делит исходный треугольник на 2 ему подобных.
• Длина искомой высоты соответствует отношению произведения катетов к линейному значению гипотенузы: h = (a * b) / c.
• Если медиана проведена из угла прямого типа, то она эквивалентна 1/2 гипотенузы. Кроме того, ее основание совпадает с центром описанной около Δ окружности, радиус которой равен медиане.
• Радиус вписанного круга в Δ эквивалентен соотношению r = (a + b — c) / 2.
• Размерность прямоугольного Δ или площадь S соответствуют величине, равной 1/2 от произведения катетов: S = (1/2) * a * b.

Следует отметить, что величину размерности можно найти из производных формул: S = (1/2) * c^2 * sin(∠CBA) * sin(∠BAC) = (1/2) * c^2 * sin(∠CBA) * cos(∠CBA) = (1/2) * c^2 * sin(∠BAC) * cos(∠BAC) = (1/2) * a^2 * tg(∠BAC) = (1/2) * a^2 * ctg(∠CBA).

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Примеры решения задач

Для закрепления теоретических знаний специалисты рекомендуют решить несколько задач. Они делятся на простые и сложные. Первые решаются при помощи одной или нескольких элементарных операций. Таких примеров в интернете очень много. Однако попадаются и сложные варианты, которые позволяют использовать полученные знания на все 100%.

В интернете встречаются онлайн-приложения, позволяющие найти решение. Этот инструмент нужно использовать для проверки результата. Хотя многие им злоупотребляют, а затем не получают правильного результата. Для начала необходимо взять готовый решенный пример и ознакомиться с ним. Далее попытаться воспроизвести его на бумаге. Подсматривать в исходник нельзя. При помощи такого приема происходит формирование алгоритма решения в головном мозге.

Сложное задание

Условие задачи следующее: имеется ΔMNO (∠MNO = 90) с высотой NP и стороной NM = 3, а также с известным значением тригонометрической функции cos между большим катетом и гипотенузой (cos(∠NOM) = (35)^(1/2) / 6). Следует найти OP. Для этого необходимо следовать такому алгоритму:

• Найти sin(∠NOM): [sin(∠NOM)]^2 + [cos(∠NOM)]^2 = 1. Отсюда следует, что sin(∠NOM) = [1 — [cos(∠NOM)]^2]^(1/2) = [1 — 35/36]^(1/2) = 1/6.
• Вычислить длину гипотенузы: MO = MN / (sin(∠NOM)) = 3 / 1/6 = 18 (ед).
• Рассмотреть ΔMNP: MN = 3, sin(∠NOM) = sin(∠MNP) = 1/6.
• Найти MP: MP = MN * sin(∠MNP) = 3 * 1/6 = 1/2.
• Искомая величина ОР высчитывается таким образом: OP = MO — MP = 18 — 1/2 = 17,5 (ед).

На основании пятого пункта можно сделать вывод, что длина искомого отрезка равна 17,5 (ед). Если проанализировать решение упражнения, то станет понятно, что очень часто применяются соотношения на основе тригонометрических функций.

Уровень турбо

В некоторых источниках задачи повышенной сложности называют «для турбо». К ним принадлежат все типы, которые имеют минимальный объем известных данных. Пусть дан равнобедренный ΔSTU (∠STU = 90). Гипотенуза на 2 больше катета. Необходимо найти его высоту TV, проведенную из прямого угла. Решение следует выполнять по такой инструкции:

• Обозначить катет неизвестной «y», тогда ST = TU = y и SU = y + 2.
• Записать формулу определения высоты: h = (a * b) / c.
• Составить уравнение: (y + 2) = y^2 + y^2.
• Раскрыть скобки и привести подобные слагаемые: y^2 + 4 * y + 4 — 2 * y^2 = -y^2 + 4 * y + 4 = y^2 — 4 * y — 4 = 0.
• Найти величину дискриминанта: D = 16 + 16 = 32.
• Первый корень: y1 = [-4 — 32^(1/2)] / 2 = [-4 — 4 * 2^(1/2)] / 2.
• Второй: [-4 + 4 * 2^(1/2)] / 2 = -2 + 2 * 2^(1/2).
• Первый не подходит, поскольку является величиной отрицательной.
• ST = TU = -2 + 2 * 2^(1/2) и SU = -2 + 2 * 2^(1/2) + 2 = 2 * 2^(1/2).
• Расчет высоты TV: TV = (-2 + 2 * 2^(1/2))^2 / 2 * 2^(1/2) = (4 — 8 * 2^(1/2) + 2) / 2 * 2^(1/2) = (6 — 8 * 2^(1/2)) / 2 * 2^(1/2) = 3 — 4 * 2^(1/2) / 2^(1/2) (ед).

Следует отметить, что в скобках необходимо указывать единицу измерения. Если размерность последней не дана, то нужно указывать ее условно.

Таким образом, для решения сложных задач по геометрии следует знать формулу высоты в прямоугольном треугольнике. Это позволяет оптимизировать решение и не совершать ошибок при вычислениях.

Видео:Зачем нужны синусы и косинусы?Скачать

Свойства высоты прямоугольного треугольника

В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.

Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Свойства высоты в прямоугольном треугольнике

Свойство 1

В прямоугольном треугольнике две высоты (h₁ и h₂) совпадают с его катетами.

Третья высота (h₃) опускается на гипотенузу из прямого угла.

Свойство 2

Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.

Свойство 3

Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

Аналогичным образом доказывается, что ∠ABD = ∠DAC.

Свойство 4

В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:

1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:

2. Через длины сторон треугольника:

Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :

Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Пример задачи

Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.

Решение
Воспользуемся первой формулой, представленной в Свойстве 4:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.

Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.

Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:

Видео:Нахождение стороны прямоугольного треугольникаСкачать

Высота в прямоугольном треугольнике

Вспомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.

В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.

Один из типов экзаменационных задач банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:

Высота проведена к гипотенузе . Она делит треугольник на два прямоугольных треугольника — и . Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.

Мы помним, что сумма двух острых углов прямоугольного треугольника равна . Значит, , то есть угол равен углу . Аналогично, угол равен углу .

Иными словами, каждый из трех углов треугольника равен одному из углов треугольника (и треугольника ). Треугольники и называются подобными. Давайте нарисуем их рядом друг с другом.

Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?

Возьмем треугольники и . Стороны треугольника длиннее, чем стороны треугольника в раз:

При решении задач нам пригодится равенство углов треугольников и , а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту.

Ты нашел то, что искал? Поделись с друзьями!

1. В треугольнике угол равен , — высота, , . Найдите .

Рассмотрим треугольник . В нем известны косинус угла и противолежащий катет . Зная синус угла , мы могли бы найти гипотенузу . Так давайте найдем :

(поскольку значение синуса острого угла положительно). Тогда:

Рассмотрим прямоугольный треугольник , . Поскольку

2. В треугольнике угол равен , , . Найдите высоту .

Сделайте чертеж и рассмотрите прямоугольный треугольник .

3. В треугольнике угол равен , , . К гипотенузе проведена высота . Найдите .

Это чуть более сложная задача. Ведь вам неизвестны катеты и .

Зато можно записать теорему Пифагора: .

Нам известно также, что:

Решая эту систему из двух уравнений, найдем:

Запишем площадь треугольника АВС двумя способами:

Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений.

📹 Видео

Высота прямоугольного треугольникаСкачать

Урок СИНУС, КОСИНУС И ТАНГЕНС ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКАСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

ТРИГОНОМЕТРИЯ с нуля — Синус, косинус, тангенс и котангенс острого углаСкачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Высота прямоугольного треугольника #огэ #математика #огэматематика #данирСкачать

Решение прямоугольных треугольников. Синус, косинус, тангенс, котангенс. Решение задачСкачать

Тригонометрия: Как запомнить? + ПОЛУЧИ ПОДАРОК от Ольги АлександровныСкачать

Синус угла 📐 Полезный файлик в комментах #математика #огэ #огэматематикаСкачать

Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать