Выпуклый и невыпуклый треугольник (4 видео)

Выпуклый многоугольник

Содержание

Определение
Геометрическая фигура многоугольник
Основные понятия
Виды фигур
Треугольник
Четырехугольник
Видео
Многоугольники
Видео

Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Определение

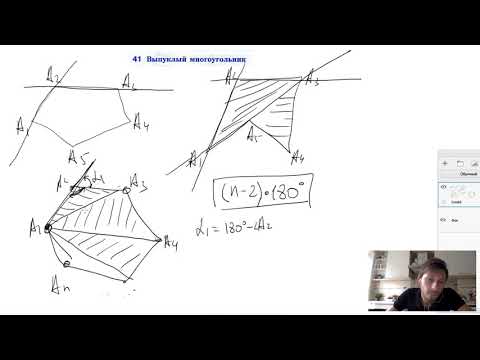
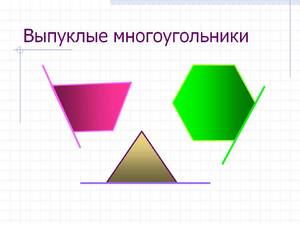
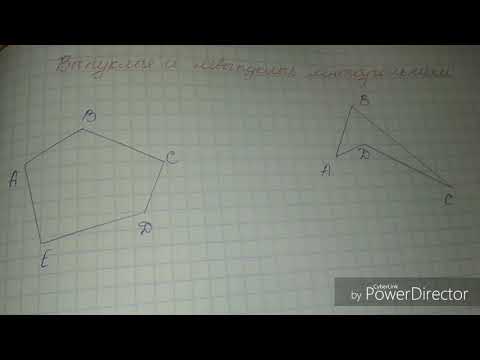
Выпуклый многоугольник — это многоугольник, лежащий по одну сторону от каждой
прямой проходящей через два его соседних угла.

Правильный многоугольник — это выпуклый многоугольник,
в котором все углы и стороны равны.

Если в многоугольнике, через каждые два его соседних угла по одну сторону
проходит прямая, то многоугольник выпуклый. Многоугольник, который не
является выпуклым называется не выпуклым многоугольником.

В выпуклых многоугольниках сумма углов вычисляется по формуле: (n-2) * 180,
где n — количество сторон.

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Геометрическая фигура многоугольник

Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.

Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.

Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.

Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.

Видео:Выпуклые и невыпуклые многоугольникиСкачать

Основные понятия

Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:

Если вершины являются концами одной стороны, они называются соседними.
Если отрезок соединяет между собой несоседние вершины, то он имеет название диагонали. У треугольника не может быть диагоналей.
Внутренний угол — это угол при одной из вершин, который образован двумя его сторонами, сходящимися в этой точке. Он всегда располагается во внутренней области геометрической фигуры. Если многоугольник невыпуклый, его размер может превосходить 180 градусов.
Внешний угол при определенной вершине — это угол смежный с внутренним при ней же. Иными словами, внешним углом можно считать разность между 180° и величиной внутреннего угла.
Сумма величин всех отрезков носит название периметра.
Если все стороны и все углы равны — он носит название правильного. Правильными могут быть только выпуклые.

Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:

Многоугольник называется плоским, если ограничивает конечную часть плоскости. Эта геометрическая фигура может быть вписанной в окружность или описанной вокруг окружности.
Выпуклым называется n-угольник, который соответствует одному из условий, приведенных ниже.
Фигура расположена по одну сторону от прямой линии, которая соединяет две соседних вершины.
Эта фигура служит общей частью или пересечением нескольких полуплоскостей.
Диагонали располагаются внутри многоугольника.
Если концы отрезка располагаются в точках, которые принадлежат многоугольнику, весь отрезок принадлежит ему.
Фигура может называться правильной, если у нее все отрезки и все углы равны. Примерами могут служить квадрат, равносторонний треугольник или правильный пятиугольник.
Если n-угольник невыпуклый, все стороны и углы его равны, а вершины совпали с таковыми правильного n-угольника, он называется звездчатым. У таких фигур могут иметься самопересечения. Примерами могут служить пентаграмма или гексаграмма.
Треугольник или четырехугольник называется вписанным в окружность, когда все его вершины располагаются внутри одной окружности. Если же стороны этой фигуры имеют точки соприкосновения с окружностью, это многоугольник описанным около некоторой окружности.

Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.

Видео:1002 Выпуклые и невыпуклые многоугольникиСкачать

Виды фигур

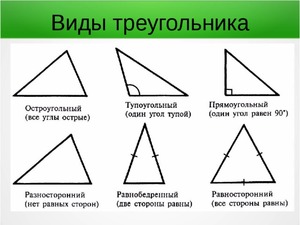
Треугольник

Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.

Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.

По соотношениям между сторонами все треугольники можно подразделять на несколько видов:

Равносторонние — у которых длина всех отрезков одинаковая.
Равнобедренные — треугольники, у которых равны два отрезка из трех.
Разносторонние — если длина всех отрезков разная.

Кроме того, принято различать следующие треугольники:

Остроугольные.
Прямоугольные.
Тупоугольные.

Четырехугольник

Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.

Если все углы четырехугольника прямые — эта фигура называется прямоугольником.
Прямоугольник, у которого все стороны имеют одинаковую величину, называется квадратом.
Четырехугольник, все стороны которого равны, называется ромбом.

На одной прямой не может находиться сразу три вершины четырехугольника.

Видео:Выпуклый многоугольник | Геометрия 7-9 класс #40 | ИнфоурокСкачать

Видео

Дополнительную информацию о многоугольниках вы найдете в этом видео.

» width=»560″ height=»314″ allowfullscreen=»allowfullscreen»>

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Многоугольники

На этом уроке мы приступим уже к новой теме и введем новое для нас понятие «многоугольник». Мы рассмотрим основные понятия, связанные с многоугольниками: стороны, вершины углы, выпуклость и невыпуклость. Затем докажем важнейшие факты, такие как теорема о сумме внутренних углов многоугольника, теорема о сумме внешних углов многоугольника. В итоге, мы вплотную подойдем к изучению частных случаев многоугольников, которые будут рассматриваться на дальнейших уроках.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»