Всякий равнобедренный треугольник остроугольный (4 видео)

Всякий равнобедренный треугольник остроугольный

Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) Боковые стороны любой трапеции равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Существуют три прямые, которые проходят через одну точку» — верно, так как через одну точку на плоскости можно провести бесконечное количество прямых.

2) «Боковые стороны любой трапеции равны» — неверно, боковые стороны равнобедренной трапеции равны.

3) «Сумма углов равнобедренного треугольника равна 180 градусам» — верно, сумма углов любого треугольника равна 180 градусам.

Содержание

Всякий равнобедренный треугольник остроугольный
Остроугольный треугольник — виды, свойства и признаки
Виды, признаки и свойства остроугольных треугольников
Равносторонний треугольник
Разносторонний треугольник
Равнобедренный остроугольный треугольник
Равнобедренный тупоугольный треугольник
🎥 Видео

Видео:Всякий равносторонний треугольник является равнобедренным. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Всякий равнобедренный треугольник остроугольный

Задание 20. Какое из следующих утверждений верно?

1) У любой трапеции боковые стороны равны.

2) Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.

3) Всякий равнобедренный треугольник является остроугольным.

1) Нет, стороны у трапеции могут быть разными по длине.

2) Да, площадь ромба можно найти по такой формуле.

3) Нет, равнобедренный треугольник может быть и прямоугольным и тупоугольным.

Видео:Всякий равнобедренный треугольник является остроугольным. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Остроугольный треугольник — виды, свойства и признаки

Одна из центральных тем на уроках геометрии – остроугольный треугольник, составная часть своих более сложных аналогов и иных тригонометрических форм.

Азы изучения точной науки начинаются с рассмотрения уникальной комбинации из трех сторон и острых углов.

Видео:Всякий равносторонний треугольник является остроугольным. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Виды, признаки и свойства остроугольных треугольников

Трехсторонние фигуры разделяются на множество подвидов и категорий.

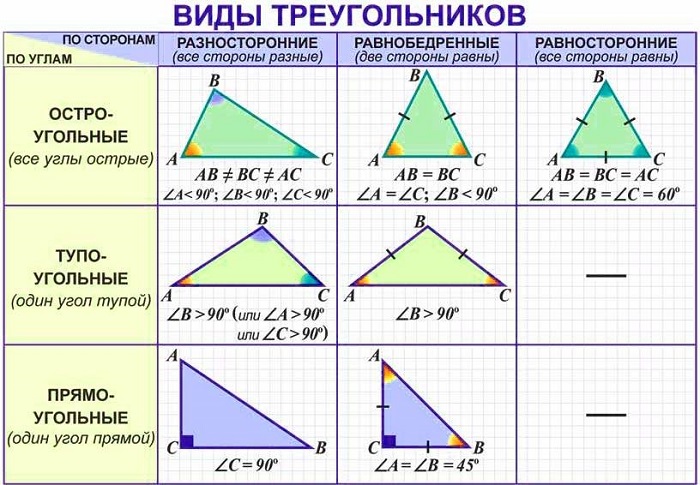
Общая классификация по наибольшему углу делит их на 3 группы:

Они располагают как общими для формы с тремя сторонами характеристиками, так и специфическими признаками.

3 угла, сумма которых равна 180°, (величина каждого меньше 90°) и 3 стороны;

сумма длин любых двух сторон больше оставшейся третьей.

Свойства остроугольной фигуры определяются вспомогательными геометрическими линиями, всегда находящимися внутри него:

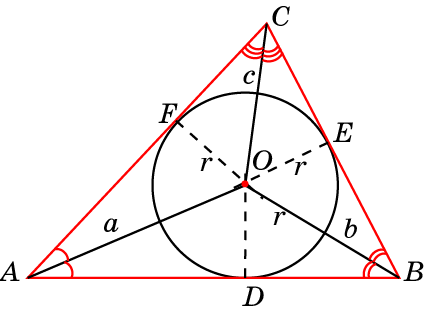
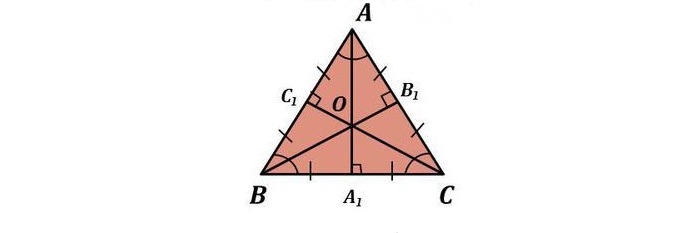
1. Биссектрисы, делящие углы пополам, являются центром, вокруг которого можно нарисовать вписанную окружность.

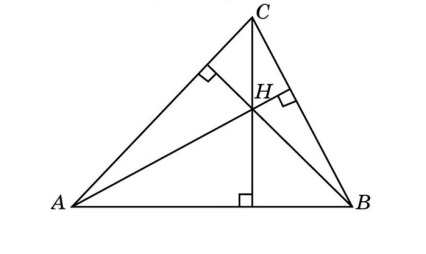
2. Высоты пересекаются в одной точке, образуя ортоцентр.

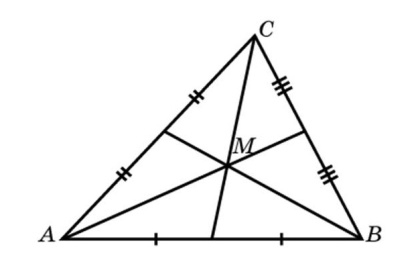
3. Медианы в точке пересечения пролегают в пропорции 2:1 (2 трети до центра и 1 треть после).

Уникальные особенности зависят от разновидностей фигуры.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Равносторонний треугольник

«Идеальный» правильный треугольник, облегчающий решение задач. Определение, форма и свойства данной геометрической формы исходят из названия — все углы равны 60°, а стороны равны друг другу.

Полное равенство придает и другую особенность: медианы, биссектрисы и высоты полностью совпадают.

Видео:Каждая из биссектрис равнобедренного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Разносторонний треугольник

Наиболее часто встречаемый на чертежах в геометрии вариант, один из самых трудноразрешимых видов. Разносторонними бывают и прямоугольные, и тупоугольные фигуры.

Уникальных отличий не имеет, только общие:

все параметры имеют разные значения;

совпадений между вспомогательными линиями нет.

Видео:Каждая из биссектрис равнобедренного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Равнобедренный остроугольный треугольник

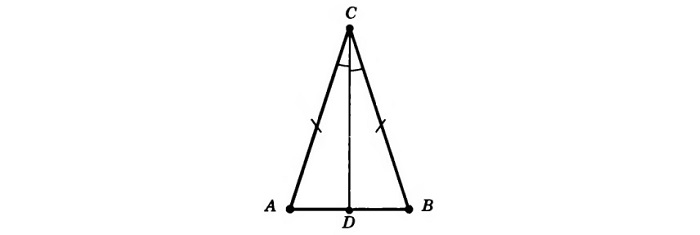
Здесь при основании (стороне, не равной остальным) находятся равные друг другу 2 стороны и 2 угла. Выглядит как вытянутый в одну сторону равносторонний треугольник.

проведенная к основанию линия – и биссектриса, и высота, и медиана;

вспомогательные линии из крайних точек при основании совпадают.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Равнобедренный тупоугольный треугольник

Пусть он и называется равнобедренным, но из-за наличия угла более 90° не является остроугольным и является представителем другой группы.

Начертить его сложнее (рисунок следует начинать с основания и 2 острых углов и уже после создавать тупой), но процесс решения и изучения прост.

Отличие у него одно – точка пересечения двух высот, проведенных от углов при основании, выходит за периметр треугольника. Чтобы ее обозначить, необходимо нарисовать «продолжения» равнобедренных линий. Все остальные свойства совпадают.

В ключевых и фундаментальных разделах математики именно треугольник является основой для доказательства многих теорем и помощью в решении множества задач. Твердое знание его свойств откроет путь к успехам в расчетах, вычислениях, оформлении чертежей и фото в проектных работах.