- Типы треугольников
- По величине углов
- По числу равных сторон
- Вершины углы и стороны треугольника
- Свойства углов и сторон треугольника
- Теорема синусов
- Теорема косинусов
- Теорема о проекциях
- Формулы для вычисления длин сторон треугольника
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- Биссектрисы треугольника
- Свойства биссектрис треугольника:
- Формулы биссектрис треугольника
- Высоты треугольника
- Свойства высот треугольника
- Формулы высот треугольника
- Окружность вписанная в треугольник
- Свойства окружности вписанной в треугольник
- Формулы радиуса окружности вписанной в треугольник
- Окружность описанная вокруг треугольника
- Свойства окружности описанной вокруг треугольника
- Формулы радиуса окружности описанной вокруг треугольника
- Связь между вписанной и описанной окружностями треугольника
- Средняя линия треугольника
- Свойства средней линии треугольника
- Периметр треугольника
- Формулы площади треугольника
- Формула Герона
- Равенство треугольников
- Признаки равенства треугольников
- Первый признак равенства треугольников — по двум сторонам и углу между ними
- Второй признак равенства треугольников — по стороне и двум прилежащим углам
- Третий признак равенства треугольников — по трем сторонам
- Подобие треугольников
- Признаки подобия треугольников
- Первый признак подобия треугольников
- Второй признак подобия треугольников
- Третий признак подобия треугольников
- Основные факты о треугольниках
- Готовьтесь к экзамену вместе с образовательным порталом «Школково»
- Все, что нужно знать о треугольнике
- ТРЕУГОЛЬНИК.
- Площадь треугольника.
- Медиана треугольника
- Биссектриса треугольника
- Высота треугольника
- Теорема синусов:
- Прямоугольный треугольник
- Соотношение элементов в прямоугольном треугольнике:
- Равнобедренный треугольник.
- Правильный треугольник
- Средняя линия треугольника
- Внешний угол треугольника
- Признаки равенства треугольников:
- Признаки подобия треугольников:
- Теорема Менелая
- 🎦 Видео
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Типы треугольников
По величине углов
По числу равных сторон
Видео:ЕГЭ 2024. ВСЁ ПРО ТРЕУГОЛЬНИКИ за 15 минутСкачать

Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Видео:Треугольники. 7 класс.Скачать

Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Видео:Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать

Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Видео:Неравенства треугольника. 7 класс.Скачать

Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Видео:Признаки равенства треугольников. 7 класс.Скачать

Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Связь между вписанной и описанной окружностями треугольника
Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
Видео:Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Основные факты о треугольниках
Определения
Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от (0^circ) до (180^circ) включительно.
Угол (alpha) называется острым, если (0^circ , прямым – если (alpha=90^circ) , тупым – если (90^circ , и развернутым – если (alpha=180^circ) .
Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.
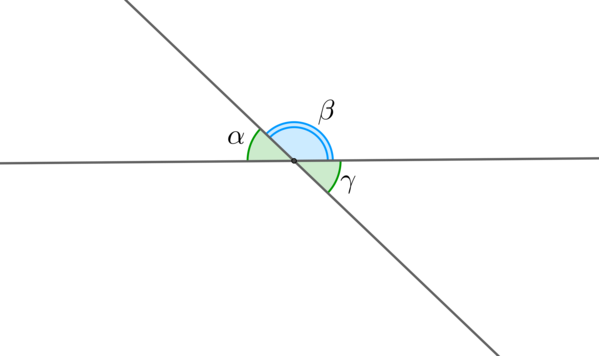
Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.
Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.
Теорема
Смежные углы (alpha) и (beta) в сумме дают (180^circ) .
Вертикальные углы равны: (alpha=gamma) .
Определения
Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.
Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.
Теоремы: признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Определение
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Две прямые называются перпендикулярными, если угол между ними равен (90^circ) .
Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом (90^circ) .
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Замечание
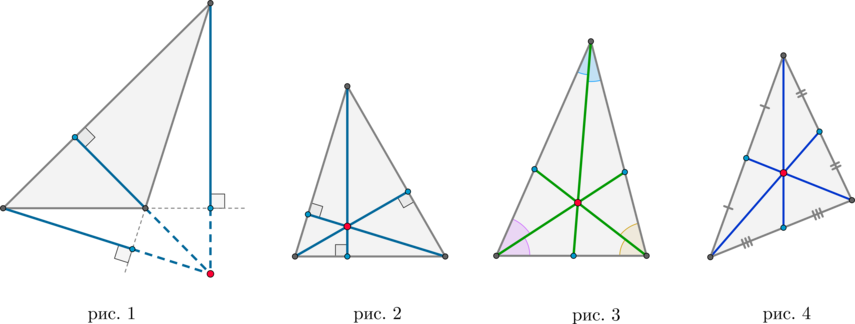
Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
Определение
Две различные прямые на плоскости называются параллельными, если они не пересекаются.
Замечание
Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.
Аксиома параллельных прямых
Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.
Следствия из аксиомы
1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.
2. Две прямые, параллельные третьей прямой, параллельны.
Теоремы: признаки параллельности прямых
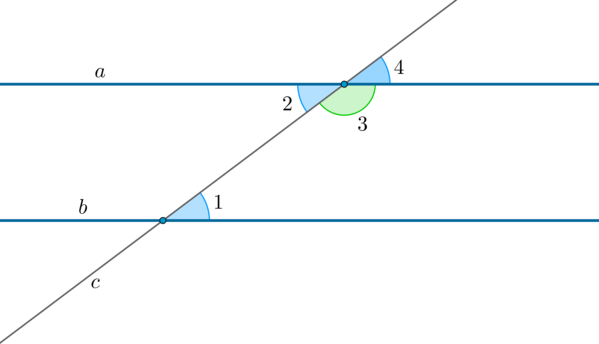
1. Если при пересечении двух прямых (a) и (b) секущей (c) накрест лежащие углы равны: (angle 1=angle 2) , то такие прямые параллельны.
2. Если при пересечении двух прямых (a) и (b) секущей (c) сумма односторонних углов (angle 1) и (angle 3) равна (180^circ) , то такие прямые параллельны.
3. Если при пересечении двух прямых (a) и (b) секущей (c) соответственные углы равны: (angle 1=angle 4) , то такие прямые параллельны.
Теоремы: свойства параллельных прямых
1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна (180^circ) .
3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Определения
Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).
Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).
Теорема
Сумма внутренних углов треугольника равна (180^circ) .
Доказательство
Рассмотрим произвольный треугольник (ABC) и покажем, что (angle A + angle B + angle C = 180^circ) .
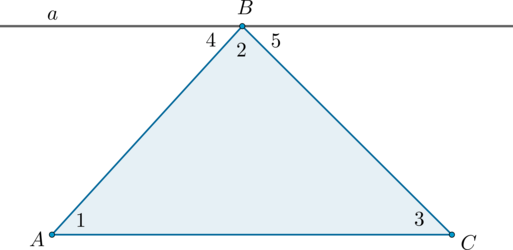
Проведём через вершину (B) прямую (a) , параллельную стороне (AC) .
Углы (1) и (4) являются накрест лежащими углами при пересечении параллельных прямых (a) и (AC) секущей (AB) , а углы (3) и (5) – накрест лежащими углами при пересечении тех же параллельных прямых секущей (BC) . Поэтому [begin &angle 4 = angle 1, angle 5 = angle 3. qquad qquad qquad (1) end]
Очевидно, сумма углов (4, 2) и (5) равна развёрнутому углу с вершиной (B) , то есть (angle 4 + angle 2 + angle 5 = 180^circ) . Отсюда, учитывая равенства ((1)) , получаем: (angle 1 + angle 2 + angle 3 = 180^circ) .
Определение
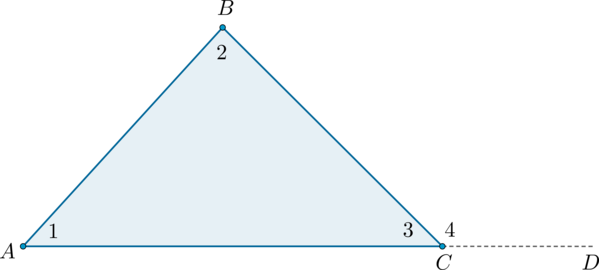
Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.
Теорема
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: (angle BCD=angle BAC+angle ABC) .
Доказательство
Угол (4) – внешний угол треугольника, смежный с углом (3) . Так как (angle 4 + angle 3 = 180^circ) , а по теореме о сумме углов треугольника (angle 1 + angle 2 + angle 3 = 180^circ) , то (angle 4 = angle 1 + angle 2) , что и требовалось доказать.
Определения
Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.
Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.
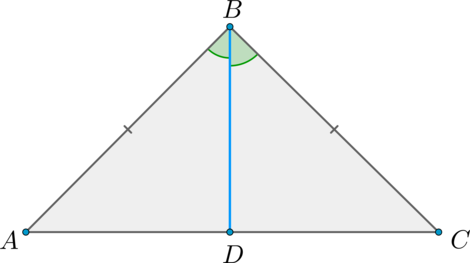
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Доказательство
Пусть (ABC) – равнобедренный треугольник, (AB = BC) , (BD) – биссектриса (проведённая к основанию).
Рассмотрим треугольники (ABD) и (BCD) : (AB = BC) , (angle ABD = angle CBD) , (BD) – общая. Таким образом, (triangle ABD = triangle BCD) по двум сторонам и углу между ними.
Из равенства этих треугольников следует, что (AD = DC) , следовательно, (BD) – медиана.
Кроме того, в равных треугольниках против равных сторон лежат равные углы, а (AB = BC) , следовательно, [begin &angle ADB = angle CDB, qquad qquad qquad (2) end] но (angle ADB + angle CDB = angle ADC) – развёрнутый, следовательно, (angle ADB + angle CDB = 180^circ) , откуда при учёте ((2)) : (angle ADB = 90^circ = angle CDB) , то есть (BD) – высота.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
В равнобедренном треугольнике углы при основании равны.
Доказательство
Проведем биссектрису (BD) (см. рисунок из предыдущей теоремы). Тогда (triangle ABD=triangle CBD) по первому признаку, следовательно, (angle A=angle C) .
Теоремы: признаки равнобедренного треугольника
1. Если в треугольнике два угла равны, то треугольник равнобедренный.
2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.
Теорема о соотношении между сторонами и углами треугольника
В треугольнике против большей стороны лежит больший угол.
В треугольнике против большего угла лежит большая сторона.
Теорема: неравенство треугольника
В треугольнике сумма любых двух сторон больше третьей стороны.
Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.
Определения
В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.
Теоремы: свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна (90^circ) .
2. В прямоугольном треугольнике катет, лежащий против угла (30^circ) , равен половине гипотенузы.
Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла (30^circ) .
Подготовка выпускников к сдаче ЕГЭ, как правило, начинается с повторения базовой теории по планиметрии, в том числе и по теме «Треугольники». Знакомство учащихся с этим разделом геометрии начинается еще в средней школе. Неудивительно, что потребность в повторении основных правил и теории по теме «Треугольник» возникает у многих выпускников. При этом решать планиметрические задачи обязательно должны уметь все учащиеся. Подобные задания включены как в базовый, так и в профильный уровень аттестационного испытания. Разобравшись с теорией и практическими упражнениями, в том числе и на вычисление вертикальных углов треугольника, старшеклассники смогут решать задачи с любым количеством действий и рассчитывать на получение конкурентных баллов по итогам сдачи ЕГЭ.
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Готовьтесь к экзамену вместе с образовательным порталом «Школково»
Занимаясь перед сдачей ЕГЭ, многие учащиеся сталкиваются с проблемой поиска базовой теории по геометрии о треугольниках. Школьных учебников в нужный момент может просто не оказаться под рукой. А найти необходимые формулы иногда оказывается достаточно сложно даже в Интернете.
Вместе с образовательным порталом «Школково» выпускники смогут качественно подготовиться к сдаче аттестационного испытания. Вся базовая теория о равнобедренных и прямоугольных треугольниках систематизирована и изложена нашими специалистами с учетом богатого опыта в максимально доступной форме. Изучив представленную информацию, школьники смогут вспомнить материал, который вызывает определенные затруднения.
Чтобы хорошо подготовиться к экзамену, учащимся, проживающим в Москве и других городах России, необходимо не только повторить теорию о прямоугольных и равнобедренных треугольниках, но и попрактиковаться в выполнении соответствующих упражнений. Задачи по данной теме вы можете найти в разделе «Каталог». Для каждого задания наши специалисты прописали подробный ход решения и указали правильный ответ. Последовательно выполняя простые и более сложные упражнения по данной теме, учащиеся смогут научиться применять на практике теоремы равенства треугольников и другую теорию, которую необходимо усвоить при подготовке к ЕГЭ. Перечень заданий в соответствующем разделе постоянно дополняется и обновляется.
Попрактиковаться в решении задач, в которых применяется теория смежных углов и другие теоремы, школьники могут в режиме онлайн.
По желанию учащегося любое упражнение можно сохранить в «Избранное». Еще раз повторив базовую теорию о прямоугольных и равнобедренных треугольниках, выпускник может в дальнейшем вернуться к заданию, которое вызвало затруднения, и обсудить алгоритм его решения с преподавателем.
Видео:Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

Все, что нужно знать о треугольнике

- Сделать чертеж. Чертеж должен максимально соответствовать условию задачи, так его основная задача помочь найти ход решения
- Нанести все данные из условия задачи на чертеж
- Выписать все геометрические понятия, которые встречаются в задаче
- Вспомнить все теоремы, которые относятся к этим понятию
- Нанести на чертеж все соотношения между элементами геометрической фигуры, которые следуют из этих теорем
Например, если в задаче встречается слова биссектриса угла треугольника, нужно вспомнить определение и свойства биссектрисы и обозначить на чертеже равные или пропорциональные отрезки и углы.
В этой статье вы найдете основные свойства треугольника, которые необходимо знать для успешного решения задач.
ТРЕУГОЛЬНИК.
Площадь треугольника.
1. 
здесь 

2. 
здесь 

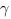
3. Формула Герона:
— здесь 

4. 
здесь 

Пусть 
Тогда формулу Герона можно записать в таком виде:
5.
6. 
здесь 

Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла делит треугольник на два треугольника, площади которых относятся как m:n:
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Медиана треугольника
— это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.
Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший — радиусу описанной окружности.

Длина медианы произвольного треугольника вычисляется по формуле:

здесь 


Биссектриса треугольника
— это отрезок биссектрисы любого угла треугольника, соединяющий вершину этого угла с противоположной стороной.
Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам:
Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.
Все точки биссектрисы угла равноудалены от сторон угла.
Высота треугольника
— это отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону, или ее продолжение. В тупоугольном треугольнике высота, проведенная из вершины острого угла лежит вне треугольника.
Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
Чтобы найти высоту треугольника, проведенную к стороне 
Центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника.
Радиус описанной окружности треугольника можно найти по таким формулам:
— здесь 


где 

Неравенство треугольника
Каждая сторона треугольника меньше суммы и больше разности двух других.
Сумма длин любых двух сторон всегда больше длины третьей стороны:

Напротив большей стороны лежит больший угол; напротив большего угла лежит большая сторона:
Если 


Теорема синусов:
стороны треугольника пропорциональны синусам противолежащих углов:
Теорема косинусов:
квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними:
Прямоугольный треугольник
— это треугольник, один из углов которого равен 90°.
Сумма острых углов прямоугольного треугольника равна 90°.
Гипотенуза — это сторона, которая лежит против угла 90°. Гипотенуза является наибольшей стороной.
Теорема Пифагора:
квадрат гипотенузы равен сумме квадратов катетов:
Радиус окружности, вписанной в прямоугольный треугольник, равен

здесь 

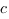
Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы:
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
Определение синуса, косинуса , тангенса и котангенса прямоугольного треугольника смотрите здесь.
Соотношение элементов в прямоугольном треугольнике:
Квадрат высоты прямоугольного треугольника, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу:
Квадрат катета равен произведению гипотенузы на проекцию катета на гипотенузу:

Катет, лежащий против угла 
Равнобедренный треугольник.
Биссектриса равнобедренного треугольника, проведенная к основанию является медианой и высотой.
В равнобедренном треугольнике углы при основании равны.






Внимание! Высота, биссектриса и медиана, проведенные к боковой стороне не совпадают.
Правильный треугольник
(или равносторонний треугольник ) — это треугольник, все стороны и углы которого равны между собой.
Площадь правильного треугольника равна

где 
Центр окружности, вписанной в правильный треугольник, совпадает с центром окружности, описанной около правильного треугольника и лежит в точке пересечения медиан.
Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший — радиусу описанной окружности.
Если один из углов равнобедренного треугольника равен 60°, то этот треугольник правильный.
Средняя линия треугольника
— это отрезок, соединяющий середины двух сторон.
На рисунке DE — средняя линия треугольника ABC.
Средняя линия треугольника параллельна третьей стороне и равна ее половине: DE||AC, AC=2DE
Внешний угол треугольника
— это угол, смежный какому либо углу треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
Тригонометрические функции внешнего угла:
Признаки равенства треугольников:
1 . Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2 . Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3 Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Важно: поскольку в прямоугольном треугольнике два угла заведомо равны, то для равенства двух прямоугольных треугольников требуется равенство всего двух элементов: двух сторон, или стороны и острого угла.
Признаки подобия треугольников:
1 . Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами равны, то эти треугольники подобны.
2 . Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны.
3 . Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.
Важно: в подобных треугольниках сходственные стороны лежат против равных углов.
Теорема Менелая
Пусть прямая пересекает треугольник 


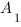

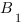

🎦 Видео
Первый признак равенства треугольников. 7 класс.Скачать

Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать

7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

9 класс, 15 урок, Решение треугольниковСкачать