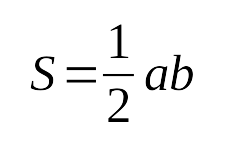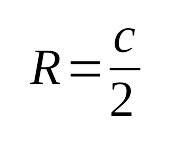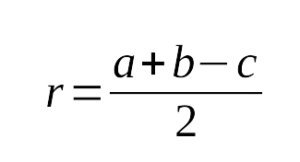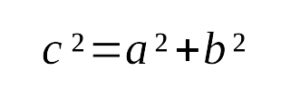Все прямоугольные треугольники подобны их

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Определение

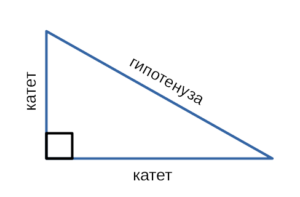
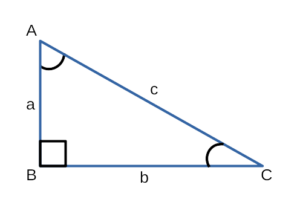
Прямоугольный треугольник — это треугольник, в котором один из углов прямой.

Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.

Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.

Видео:Все прямоугольные треугольники подобны. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Свойства прямоугольного треугольника

В прямоугольном треугольнике:

1. Сумма острых углов 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
3. Медиана, проведенная к гипотенузе, равна ее половине.
4. Центр описанной окружности — середина гипотенузы.
   

Формулы:

1. Площадь прямоугольного треугольника равна
   половине произведения катетов:
   
2. Радиус описанной окружности около прямоугольного
   треугольника равен половине гипотенузы:
   
3. Радиус вписанной окружности в прямоугольный треугольник
   выражается следующим образом:
   
4. Квадрат гипотенузы равен сумме квадратов катетов:

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Признаки равенства прямоугольных треугольников

С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.

1. По двум катетам:
   Если два катета одного прямоугольного треугольника соответственно
   равны двум катетам другого прямоугольного треугольника,
   то такие треугольники равны.
   
2. По катету и гипотенузе:
   Если катет и гипотенуза одного прямоугольного треугольника соответственно
   равны катету и гипотенузе другого прямоугольного треугольника,
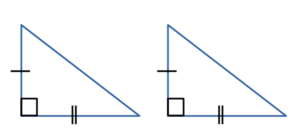
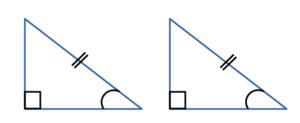
   то такие треугольники равны.
   
3. По гипотенузе и острому углу:
   Если гипотенуза и острый угол одного прямоугольного треугольника соответственно
   равны гипотенузе и острому углу другого прямоугольного треугольника,
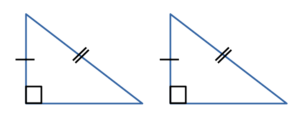
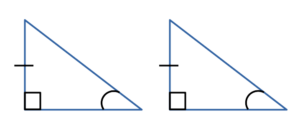
   то такие треугольникиравны.
   
4. По катету и острому углу:
   Если катет и острый угол одного прямоугольного треугольника соответственно
   равны катету и острому углу другого прямоугольного треугольника,
   то такие треугольники равны.

Видео:Подобие прямоугольных треугольников и его применениеСкачать

Признаки прямоугольного треугольника

С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.

1. По теореме Пифагора:
   Если квадрат стороны равен сумме квадратов двух других сторон,
   то треугольник прямоугольный.
2. По центру описанной окружности:
   Если центр описанной окружности лежит на стороне треугольника,
   то треугольник прямоугольный.
3. По медиане:
   Если медиана треугольника равна половине стороны, к которой она проведена,
   то треугольник прямоугольный.
4. По площади:
   Если площадь треугольника равна половине произведения двух его сторон,
   то треугольник прямоугольный.
5. По радиусу описанной окружности:
   Если радиус описанной окружности равен половине,
   то треугольник прямоугольный.

Видео:Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

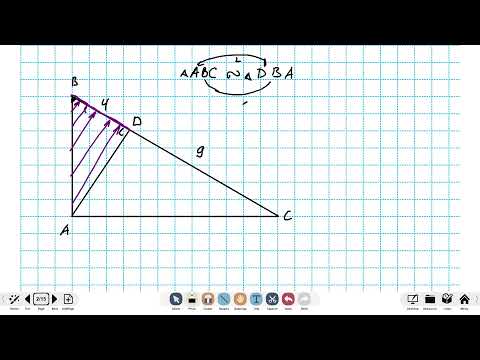
Признаки подобия прямоугольных треугольников

С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Все прямоугольные треугольники подобны их

Какое из следующих утверждений верно?

1. Все прямоугольные треугольники подобны.

2. Через заданную точку плоскости можно провести только одну прямую.

3. Диагонали ромба точкой пересечения делятся пополам.

В ответ запишите номер выбранного утверждения.

Проверим каждое из утверждений.

1) Все прямоугольные треугольники подобны — неверно, поскольку не соответствует ни одному из признаков подобия.

2) Через заданную точку плоскости можно провести только одну прямую — неверно, через две точки можно провести только одну прямую.

3) Диагонали ромба точкой пересечения делятся пополам — верно.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Все прямоугольные треугольники подобны их

Задание 20. Какое из следующих утверждений верно?

1) Все прямоугольные треугольники подобны.

2) Существует прямоугольник, диагонали которого взаимно перпендикулярны.

3) Сумма углов прямоугольного треугольника равна 90 градусам.

1) Нет, все прямоугольные треугольники имеют угол 90 градусов, но этого не достаточно для подобия.

2) Да, диагонали взаимно перпендикулярны у квадрата, это частный случай прямоугольника.

3) Нет, сумма углов в любом треугольнике 180 градусов.

💥 Видео

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Подобие в прямоугольных треугольникахСкачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Решение задач на тему "Подобные треугольники". 8 классСкачать

Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать

Подобие прямоуголных треугольников. 1 признак.Скачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать