Все о треугольнике проект

Индивидуальный учебный проект по теме «Треугольники».

В работе рассматриваются основные типы и свойства треугольников, в том числе изучение которых не входит в школьную программу.

А также изучение сведений о нахождении треугольников в окружающем мире.

Видео:Треугольники. 7 класс.Скачать

Скачать:

Видео:Треугольник проектного управления: 3 ключевых ограниченияСкачать

Предварительный просмотр:

Муниципальное образовательное учреждение

Дашковская средняя общеобразовательная школа

Итоговый проект по математике

за курс 9 класса

по теме: «Треугольники»

На протяжении всей своей сознательной жизни каждый человек проявляет неподдельный интерес к такой геометрической фигуре, как треугольник. Игра в пирамидки, складывание оригами, составление аппликации из цветной бумаги с помощью треугольных фигурок — все эти действия дают ребёнку первое представление о треугольниках. Треугольники существуют в природе, в архитектуре, в искусстве и в окружающей нас жизни.

Актуальность данного проекта определяется важностью умения видеть математику в мире, в котором мы живём, необходимостью добывать знания о треугольниках, а также применением полученных знаний в повседневной жизни.

Цель : Обобщение знаний о треугольниках, и их практическом применении.

• Изучение исторических сведений о треугольниках;
• Изучение сведений о нахождении треугольников в окружающем мире;
• Исследование свойств треугольников и применения этих свойств в решении практических задач.

Практическая значимость: данный материал способствует формированию представления о прикладных возможностях математики.

Треугольник как символ. Исторические сведения.

Треугольник является одной из первых геометрических фигур, которая стала использоваться в орнаментах древних народов.

В Древнем Египте он был прямоугольным и являлся воплощением триады духовной воли, любви и высшего разума человека. Вертикальная сторона египетского треугольника составляла три единицы длины, основание — четыре, а гипотенуза – пять.

На Древнем Востоке почитали треугольник как символ природы всего сущего. Треугольник с вершиной, соединенной с такой же геометрической фигурой, ацтеки использовали в качестве эмблемы временного цикла. В буддийской традиции два смыкающихся треугольника олицетворяют чистое пламя и Три Драгоценности Будды. Китайский символ восстановления изображается в виде треугольника с подвешенными к нему мечами.

У христиан — треугольник, образованный тремя пересекающимися окружностями, олицетворяет Троицу в единении и равенстве трех ее составляющих. Два соединенных вершинами вертикальных треугольника разделяют символизм песочных часов, олицетворяя неумолимо идущее время и смертность. Также песочные часы часто используются для обозначения благочестивого, тихого образа жизни, краткости человеческой жизни, а также применяются как атрибут отца-времени и порой даже смерти.

Начиная с ранних христиан треугольник был символом Святой Троицы. Равносторонний треугольник толковался как равенство и единая божественная сущность Бога Отца, Бога Сына и Духа Святого. Иногда этот символ составляли из трех переплетенных между собой рыб. Символ Троицы по католической традиции составлялся из трех малых треугольников, вписанных в один большой с кругами на вершинах. Три этих круга означают триединство, но каждый круг независим и совершенен сам по себе. Эта схема иллюстрировала принцип триединства и вместе с тем индивидуальности каждого составляющего Святой Троицы.

Печать Соломона — другое название звезды Давида, образованной наложением друг на друга двух треугольников, т.е. гексаграммы. По преданию, царь Соломон с помощью этого знака управлял духами, заключенными в медный сосуд. Считается, что печать Соломона является мощным амулетом, способным защитить своего обладателя от влияния злых духов.

Раздел II. Треугольник в геометрии.

Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника.

Стороны треугольника образуют в вершинах треугольника три угла, поэтому треугольник можно также определить как многоугольник, у которого имеется ровно три угла. Треугольник является одной из важнейших геометрических фигур, повсеместно используемых в науке и технике, поэтому глубокое исследование его свойств проводилось начиная с глубокой древности.

2.1.1. Основные элементы треугольника ABC

Вершины – точки A, B, и C;

Стороны – отрезки a = BC, b = AC и c = AB, соединяющие вершины;

Углы – α, β, γ образованные тремя парами сторон. Углы часто обозначают так же, как и вершины, – буквами A, B и C.

Угол, образованный сторонами треугольника и лежащий в его внутренней области, называется внутренним углом, а смежный к нему является внешним углом треугольника.

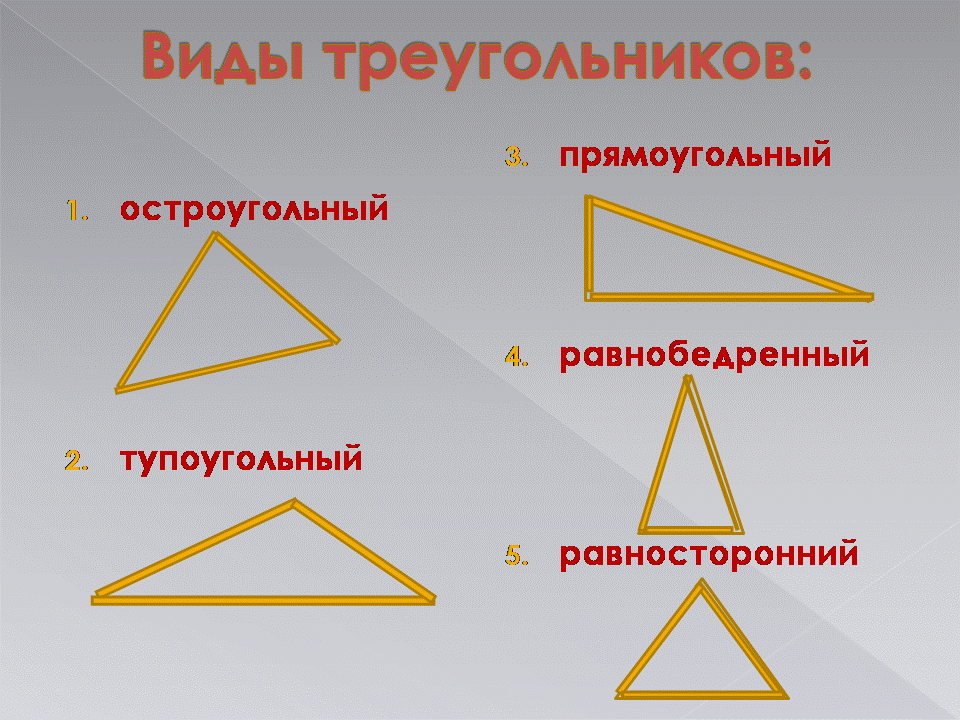
2.1.2. Виды треугольников.

Треугольник называется разносторонним , если любые две стороны его не равны друг другу.

Треугольник, все стороны которого равны, называется равносторонним.

Треугольник называется равнобедренным , если у него две стороны равны.

Треугольник называется остроугольным , если все его углы острые.

Треугольник называется тупоугольным , если один из его углов тупой.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°.

Египетский треугольник –прямоугольный треугольник с соотношением сторон 3:4:5. Особенностью треугольника, известной ещё со времён античности, является то, что при таком отношении сторон теорема Пифагора даёт целые квадраты как катетов, так и гипотенузы, то есть 9:16:25.

Название треугольнику с таким отношением сторон дали эллины. В VII — V веках до н. э. греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 до н. э. по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к формулировке и доказательству его знаменитой теоремы.
Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.
Египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов землемерами и архитекторами.
Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.. Применялся египетский треугольник в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами.

Треуго́льник Рёло́ представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло.

Треугольник Рёло является простейшей после круга фигурой постоянной ширины. То есть если к треугольнику Рёло провести пару параллельных опорных прямых, то независимо от выбранного направления расстояние между ними будет постоянным. Это расстояние называется шириной треугольника Рёло.

Среди прочих фигур постоянной ширины треугольник Рёло выделяется рядом экстремальных свойств: наименьшей площадью, наименьшим возможным углом при вершине, наименьшей симметричностью относительно центра.

Название фигуры происходит от фамилии немецкого механика Франца Рёло. Он, вероятно, был первым, кто исследовал свойства этого треугольника; также он использовал его в своих механизмах.

2.1.3. Основные свойства треугольника.

Свойства треугольника, изучающиеся в школе, за редким исключением, известны с античности.

Теорема Чевы была доказана в XI веке арабским учёным Юсуфом аль-Мутаманом ибн Худом, однако его доказательство было забыто. Она была доказана вновь итальянским математиком Джованни Чевой в 1678 году.

Дальнейшее изучение треугольника началось в XVII веке: была доказана теорема Дезарга (1636), открыты некоторые свойства точки Торричелли (1659). В XVIII веке была обнаружена прямая Эйлера и окружность шести точек (1765). В 1828 году была доказана теорема Фейербаха. В начале XIX века была открыта точка Жергонна.

Многие факты, связанные с треугольником, были открыты в конце XIX века. К этому времени относится творчество Эмиля Лемуана, Анри Брокара, Жозефа Нейберга, Пьера Сонда́.

Во всяком треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы.

Каждый внешний угол треугольника равен разности между 180° и соответствующим внутренним углом. Для внешнего угла также имеет место теорема о внешнем угле треугольника: внешний угол равен сумме двух других внутренних углов, с ним не смежных .

В треугольнике сумма длин двух его сторон больше длины третьей стороны.

Дополнительное свойство: каждая сторона треугольника больше разности двух других сторон.

Теорема о сумме углов треугольник

Сумма внутренних углов треугольника всегда равна 180°:

В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше.

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.

где R — радиус окружности, описанной вокруг треугольника.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними Является обобщением теоремы Пифагора.

Теорема о проекциях

Из теоремы о проекциях следует то, что высота, опущенная, например, из вершины С, делит противоположную ей сторону АВ на две части и , считая от вершины А к В.

Свойство «жесткости треугольника».

Треугольник — жёсткая фигура. Представим себе две рейки, у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой: сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек. Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.

Рассмотрим модели двух фигур — треугольника и четырёхугольника и выясним, можно ли, не меняя длины сторон, изменить форму фигуры? Под действием небольшой силы четырёхугольник изменил свою форму, а треугольник нет.

Вывод: можно сказать, что треугольник – не изменяющаяся фигура. В нем нельзя сдвинуть или раздвинуть никакие две стороны, в отличие от любого другого многоугольника. В треугольнике нельзя изменить ни один из углов. Таким образом, треугольник – жесткая фигура. Если заданы три его стороны, то форму треугольника уже изменить нельзя, не разрушив его. Это свойство широко используется на практике.

2.1.4. Замечательные точки треугольника

Замечательные точки треугольника — точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника.

Обычно они расположены внутри треугольника, но и это не обязательно. В частности, точка пересечения высот может находиться вне треугольника.

Замечательными точками треугольника являются точки пересечения:

Факт того, что три медианы пересекаются в одной точке, был доказан ещё Архимедом.

• Центроид делит каждую медиану в отношении 2:1, считая от вершины.
• Если в вершины треугольника поместить равные массы, то центр масс полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой массой также находится в центроиде.
• Если М — центроид треугольника , то для любой точки О верно равенство
• Центроид является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение (теорема Лейбница).
• Три отрезка прямых, соединяющих вершины треугольника с центроидом, разбивают данный треугольник на три равновеликих треугольника (равной площади).
• Три отрезка прямых, соединяющих середины сторон треугольника с центроидом, разбивают данный треугольник на три равновеликих четырёхугольника (равной площади).
• Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин: треугольника.

• Центр вписанной окружности треугольника находится на одинаковом расстоянии от всех сторон треугольника.

В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольном), вне его (в тупоугольном) или совпадать с вершиной (в прямоугольном — совпадает с вершиной при прямом угле).

• Если в четвёрке точек А, В, С, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек .

• Радиусы окружностей, проходящих через любые три точки ортоцентрической системы , равны (следствие теоремы Гамильтона для окружности Эйлера). Их часто называют окружностями Джонсона.
• Последнее утверждение можно сформулировать так: Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих равные радиусы описанных окружностей (следствие теоремы Гамильтона для окружности Эйлера). При этом одинаковый радиус этих трех окружностей равен радиусу окружности, описанной около исходного остроугольного треугольника.

• Ортоцентр лежит на одной прямой с центроидом , центром описанной окружности
• Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник .
• Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. .
• Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности .
• Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.

• Расстояние от центра описанной окружности до стороны равно . расстояние от ортоцентра до вершины равно .

Раздел III . Треугольники вокруг нас.

Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней Греции и Древнего Египта. Еще в древности стали вводить некоторые знаки обозначения для геометрических фигур.

Древнегреческий ученый Герон (I век) впервые применил знак вместо слова треугольник.

Треугольник является одной из первых геометрических фигур, которая стала использоваться в орнаментах древних народов.

Различные жилища людей: вигвам, юрта, палатка. Все они имеют конусообразную форму, в сечении получается треугольник. Такие сооружения легко обдуваются ветрами, с них быстро стекает вода. Крыши старых деревянных домов и современных многоэтажек имеют форму треугольника. Это связано с тем, что на таких крышах не задерживается талый снег и легко стекает дождевая вода.

Предметы одежды человека. Различные головные уборы: треуголки, пилотки, колпаки, косынки – имеют треугольную форму. Женские платки, прежде чем накинуть на голову, складывают пополам. При шитье юбки часто втачивают клинья, которые тоже имеют форму треугольника, что придает юбке пышность. Чтобы одежда не помялась, ее хранят на плечиках, имеющих треугольную форму.

Солдатский треугольник – письмо без марки и конверта, отправленное солдатом с фронта или солдату на фронт.

Пирами́да Хео́пса — крупнейшая из египетских пирамид , единственное из «Семи чудес света» , сохранившееся до наших дней. Строительство, продолжавшееся двадцать лет, началось около 2560 года до н. э.

На парусных судах используются паруса треугольной формы.

При создании букета или композиции нужно соблюдать гармонию цвета. При этом используется метод равностороннего треугольника .

Треугольник широко используется в предупреждающих знаках дорожного движения.

Широкое применение в жизни человека нашло свойство жесткости треугольника.

Символ Франции знаменитая Эйфелева башня — самая узнаваемая архитектурная достопримечательность Парижа. Колебания башни во время бурь не превышают 15 см. Это объясняется тем, что вся конструкция башни сплетена из треугольников, обладающих жёсткостью.

Во время Великой Отечественной войны для сохранения стекол во время бомбежки их заклеивали бумажными полосками, чтобы получился треугольник.

В основе геодезического купола лежит каркас, представляющий собой пространственную ферму в виде полусферы. Именно из треугольников и состоит основной каркас геокупола. Благодаря своей конструкции геодезические купола выдерживают нагрузки, в несколько раз превышающие допустимые нагрузки для обычных прямоугольных сооружений.

Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку. Телеграфные столбы с подпоркой называют анкерными.

Стропила зданий имеют вид треугольников. Это придаёт им крепость и устойчивость.

При строительстве любых мостов в их конструкциях также присутствуют треугольники. Треугольники делают надежными конструкции высоковольтных линий электропередач.

Свойство жесткости треугольника широко используют в практике при строительстве железных конструкций.

п.3.1. Треугольник в математике.

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел.

Треугольник Серпинского — фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Вацлавом Серпинским в 1915 году. Также известен как «салфетка» Серпинского.

Середины сторон равностороннего треугольника соединяются отрезками. Получаются 4 новых треугольника. Из исходного треугольника удаляется внутренность срединного треугольника. Получается множество Т 1 , состоящее из 3 оставшихся треугольников «первого ранга». Поступая точно так же с каждым из треугольников первого ранга, получим множество Т 2 , состоящее из 9 равносторонних треугольников второго ранга. Продолжая этот процесс бесконечно, получим бесконечную последовательность Т n , пересечение членов которой есть треугольник Серпинского.

Важным свойством треугольника Серпинского является его самоподобие — ведь он состоит из трёх своих копий, уменьшенных в два раза (это части треугольника Серпинского, содержащиеся в маленьких треугольниках, примыкающих к углам).

Если в треугольнике Паскаля все нечётные числа окрасить в чёрный цвет, а чётные — в белый, то образуется треугольник Серпинского.

п.3.2. Треугольник в астрономии.

Треуго́льник (лат. Triangulum, Tri) — созвездие северного полушария неба. Занимает на небе площадь 131,8 квадратных градуса, содержит 25 звёзд, видимых невооружённым глазом.

В Треугольнике находится спиральная галактика M33 (галактика Треугольника), третья по величине в Местной группе.

Звезды Треугольника не ярки: α всего лишь третьей звёздной величины. Всего в созвездии можно насчитать 15 звёзд. В телескоп можно увидеть и двойную звезду ι, компоненты которой окрашены в золотисто-жёлтый и зелёно-голубой цвета.

Треугольник Кеплера.
В начале XVII в. знаменитый астроном Кеплер составил диаграмму соединения планет Сатурна и Юпитера. Так в астрономии называют расположение планет, при котором для земного наблюдателя эклиптические долготы равны нулю, а сами небесные тела находятся близко друг к другу или даже перекрываются. Кеплер представил это явление в виде треугольника , который вращается по зодиакальному кругу, совершая полный оборот за 2400 лет.

п.3.3. Треугольник в музыке.

Треуго́льник (итал. triangolo, англ. и фр. triangle, нем. Triangel) — ударный музыкальный инструмент в виде металлического прута (обычно из стали или алюминия), изогнутого в форме треугольника. Один из углов оставлен открытым (концы прута почти касаются).

Треугольник принадлежит к инструментам с неопределённой высотой звука, имеет блестящий и яркий тембр, способный украсить даже мощное оркестровое tutti. Как правило, ему поручаются несложные ритмические фигуры и тремоло. Треугольник подвешивается за один из углов на тонкой проволоке или тесьме, которую держат в руке или прикрепляют к пюпитру. По треугольнику ударяют металлической (реже деревянной) палочкой (на жаргоне музыкантов эта палочка называется «гвоздь»).

Треугольную форму имеют музыкальные инструменты : балалайка, арфа, треугольник.

Треугольники окружают нас повсюду: детские пирамидки, архитектурные сооружения, дорожные знаки, музыкальные инструменты. В повседневной жизни мы почти перестали их замечать, а ведь это очень интересно, знать историю привычных для всех предметов, тем более, если она так увлекательна.

С одной стороны, треугольники имеют тысячелетнюю историю, с другой — это современный раздел математики. Теория треугольников имеет большое значение не только для теоретических исследований по геометрии, но и для других наук.

«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия». Эти слова, сказанные великим французским архитектором Ле Корбюзье, в начале ХХ века, очень точно характеризуют и наше время.

Список использованной литературы

1. Атанасян Л. С. Геометрия: Учеб. для общеобразоват. учреждений. – М.: Просвещение, 2002.
2. За страницами учебника алгебры: Кн. для учащихся 7 – 9 кл. сред. Шк. — М.: Просвещение, 1990. – 224 с.: ил.
3. Мякишев А. Г., Элементы геометрии треугольника., Москва, МЦНМО, 2002.
4. Абачиев С. К. О треугольнике Паскаля, простых делителях и фрактальных структурах // В мире науки, 1989, № 9.

Видео:ЕГЭ 2024. ВСЁ ПРО ТРЕУГОЛЬНИКИ за 15 минутСкачать

Проект по математике » Все о треугольниках»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Необъяснимые встречи | Проклятие Бермудского треугольника | DiscoveryСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Выполнила: Ученица 9кл Струговской ООШ Карцева Полина. Руководитель: Аврамец Л.Н.

Проблема: Выяснить, насколько важна данная тема при подготовке к ОГЭ. Цели: Систематизировать понятия по теме «Все о треугольниках»; Показать практическое применение данного материала при решении задач при подготовке к ОГЭ; Научиться сравнивать треугольники между собой; Выяснить, каковы особенности каждого треугольника.

Содержание Виды треугольников; Свойства треугольников; Прямоугольный треугольник; Равнобедренный треугольник; Правильный треугольник; Равенство треугольников; Медианы; Высоты; Биссектрисы; Средняя линия; Серединный перпендикуляр; Площадь треугольника; Подобие треугольников; Окружность, вписанная в треугольник; Окружность, описанная около треугольника.

Виды треугольников По углам: Тупоугольный – треугольник, у которого один из углов тупой; Остроугольный – треугольник, у которого все углы острые; Прямоугольный – треугольник, у которого один из углов прямой.

Виды треугольников По сторонам: Разносторонний – треугольник, у которого все стороны различны по длине; Равнобедренный – треугольник, у которого две стороны равны; Равносторонний – треугольник, у которого все стороны равны. Боковая сторона Боковая сторона основание Вершина равнобедренного треугольника

Свойства треугольников Сумма углов треугольника равна 1800 Внешний угол треугольника равен сумме двух внутренних, не смежных с ним, углов В любом треугольнике каждая сторона меньше суммы двух других сторон а

Краткое описание документа:

Данный материал объединяет все материалы по треугольникам за 7 класс. Данная презентация может быть использована как при изучении каждой темы в отдельности, в качестве наглядности, так и на последних уроках закрепления в конце года. Так же ее можно использовать в 8 классе для повторения в начале года, а в 9 в качестве подготовки к экзамену.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 942 человека из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 677 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 302 человека из 68 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 516 657 материалов в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

Глава 2. Треугольники

Другие материалы

• 25.04.2018
• 278
• 0

• 24.04.2018
• 6280
• 24

• 23.04.2018
• 713
• 0

• 16.04.2018
• 926
• 17

• 13.04.2018
• 512
• 0

• 13.04.2018
• 279
• 0

• 12.04.2018
• 4342
• 36

• 12.04.2018
• 9633
• 370

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 01.05.2018 2300
• PPTX 2.5 мбайт
• 28 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Аврамец Любовь Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года и 9 месяцев
• Подписчики: 19
• Всего просмотров: 88782
• Всего материалов: 134

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Петербурге введут новые COVID-ограничения для несовершеннолетних

Время чтения: 2 минуты

Каждый второй российский студент недоволен своим вузом

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Онлайн-семинар о снятии эмоционального напряжения у детей и подростков

Время чтения: 2 минуты

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Проект «Треугольники»

Цель проекта:

Наглядно продемонстрировать применение треугольников.

Задачи проекта:

1. Выяснить, что такое треугольники;

2. Рассмотреть области их применения;

3. Создать модель, наглядно демонстрирующую вывод формулы площади треугольника.

Просмотр содержимого документа
«Проект «Треугольники»»

Муниципальное казённое общеобразовательное учреждение

Баганская средняя общеобразовательная школа № 2

имени героя Советского Союза Андрея Григорьевича Матвиенко

АВТОР: Егор Бабенко,

обучающийся 7 класса

Матюшко Нина Петровна,

1.4 Треугольники в архитектуре…………………………..………………….стр.7

1.10 Знаки дорожного движения……………………………………………..стр.13

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ……………. …………. стр. 21

Наглядно продемонстрировать применение треугольников.

1. Выяснить, что такое треугольники;

2. Рассмотреть области их применения;

3. Создать модель, наглядно демонстрирующую вывод формулы площади треугольника.

1. Работа с литературой и материалами Интернет по данной теме;

2. Систематизация полученных материалов;

3. Анализ проделанной работы.

Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, трех отрезков, которые последовательно

соединяют эти точки и ограниченной ними части плоскости.

1.2 Виды треугольников

Треугольники можно классифицировать по различным критериям.

В первую очередь они делятся на остроугольные, тупоугольные, прямоугольные, равнобедренные и равносторонние.

Первые обладают острыми углами, то есть такими, которые равны менее чем 90 0 . К остроугольным треугольникам относятся также и равносторонние. У таких треугольников все стороны и углы равны. Все они равны 60 0 , это можно легко вычислить, разделив сумму всех углов (180 0 ) на три.

У тупоугольных один из углов — тупой, то есть такой, который равен более чем 90 0 , остальные два — острые.

У прямоугольного треугольника один угол равен 90 0 (прямой), то есть две из его сторон расположены перпендикулярно. Остальные два угла являются острыми. Они могут быть равными, тогда он будет равнобедренным. С прямоугольным треугольником связана теорема Пифагора. При помощи ее можно найти третью сторону, зная две первые. Согласно данной теореме, если прибавить квадрат одного катета к квадрату другого, можно получить квадрат гипотенузы. Катет — это одна из сторон треугольника, которые образуют угол в 90 0 . Гипотенуза — это оставшаяся сторона, которая расположена напротив прямого угла. Отношение прилежащего катета к гипотенузе называется не иначе как косинус, а противоположного — синус.

Треугольники в религии

На Древнем Востоке почитали треугольник как символ природы всего сущего. Треугольник с вершиной, соединенной с такой же геометрической фигурой, аптеки использовали в качестве эмблемы временного цикла. Герменевтической традиции известно множество видов треугольников, имеющих различные толкования: например, данная геометрическая фигура с горизонтальной чертой почиталась ими пассивным символом, который означает воздух, а перевернутая является олицетворением чаши, которая готова принять воду, а также соответствует женскому началу. Имя «Святой Дух» на греческом языке звучит как «pneuma», что значит буквально «дыхание», «ветер». В самой своей основе термин «Сын Божий» относится к Богу, явившемуся во плоти в образе Иисуса Христа для спасения человечества. Термин «Бог Отец» является библейским и относится к самому Богу. Бог есть Отец; но он не только Отец Сына, а Отец всего сотворенного.

Треугольники в архитектуре

Объединение художников, известное как «художественно-психологическая группа» Н. И. Кульбина. Сыграло заметную роль в формировании петербургского художественного авангарда. Впервые «Треугольник» заявил о себе на выставке «Современные течения в искусстве» в апреле 1908 г. В состав группы кроме Кульбина входили М. Андерс, Г. Бланк, М. Дружинина, Н. Гиппиус, Н. Калмаков, 3. Мостова, Л. Мейстер, А Николаев и др. Эмблемой группы сделался треугольник, стороны которого имели синий, желтый и красный цвета. Треугольник Пенроуза — одна из основных невозможных фигур, известная также под названиями невозможный треугольник и трибар.Тринадцатиметровая скульптура невозможного треугольника из алюминия была воздвигнута в 1999г. в городе Петр (Австралия).

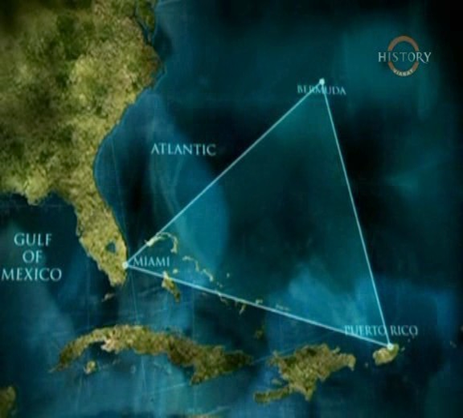
1.5 Бермудский треугольник

Обитель самого сатаны, морское кладбище, ужас Атлантики – всеми этими страшными эпитетами именуют мистическую зону в Атлантическом океане. Каждый год в Бермудском треугольнике загадочным образом исчезают корабли и самолёты. Что же это — больное воображение журналистов или по-настоящему опасная и мистическая зона, окутанная таинственностью и загадочностью?

Район ограничен линиями от Флориды до Бермудских островов, Далее к Пуэрто-Рико и назад к Флориде через Багамы. Некоторые люди считают, что эти исчезновения происходят из-за необычных погодных условий. Некоторые считаю, что это из-за похищений инопланетян!

1.6 Звезда Давида

Среди еврейского народа этот знак носит название «Маген Давид» («Щит Давида»). Мистики из Индии обозначают шестиконечной звездой сердечную чакру Анахату, в которой сочетается активное и пассивное начало. В некоторых восточных регионах значение символа связывают с богиней Астартой, которую также именуют Иштар. Гексаграмму можно встретить в средневековой алхимической и мистической литературе. Древний символ, эмблема в форме шестиконечной звезды (гексаграммы), в которой два равносторонних треугольника наложены друг на друга: верхний — вершиной вверх, нижний — вершиной вниз, образуя структуру из шести равносторонних треугольников, присоединенных к сторонам шестиугольника. Название «Звезда Давида» этот символ получил, согласно легенде, потому что гексаграмма — интернациональный символ весьма древнего происхождения. Этот знак обнаруживается в Индии, где он использовался, судя по всему, ещё задолго до того, как появился на Ближнем Востоке и в Европе.

1.7 Глаз в треугольнике

Оккультный знак «глаз в треугольнике» (или «Всевидящее око», или «сияющая дельта») считается символом Бога. Происхождение свое он ведет с глубокой древности. Возможно, традиция изображать подобным образом божество берет свое начало еще в Древнем Египте. В этом государстве часто использовался религиозный знак «соколиное око Гора». Христианская версия Ока провидения, заключённого в треугольник, символизирующий Троицу

В 1782 Око провидения было принято как часть символики обратной стороны Большой Печати Соединенных Штатов. На печати Око окружено словами «Annuit Cœptis», означающими «оно благосклонно к нашим начинаниям».

Также Всевидящим Оком может называться символическое изображение «Всевидящего Божьего глаза», вписанное в треугольник — не каноничный символ Троицы.

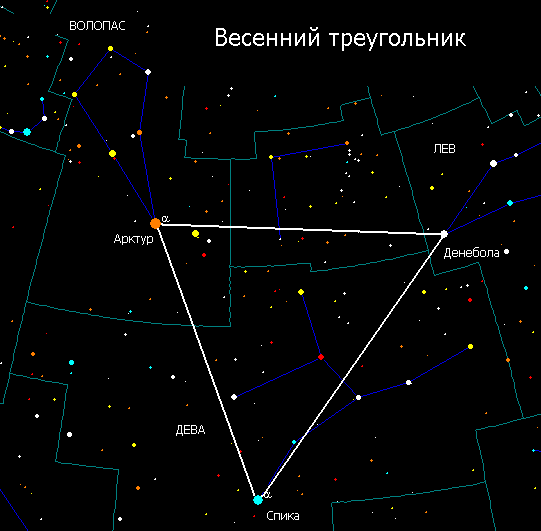
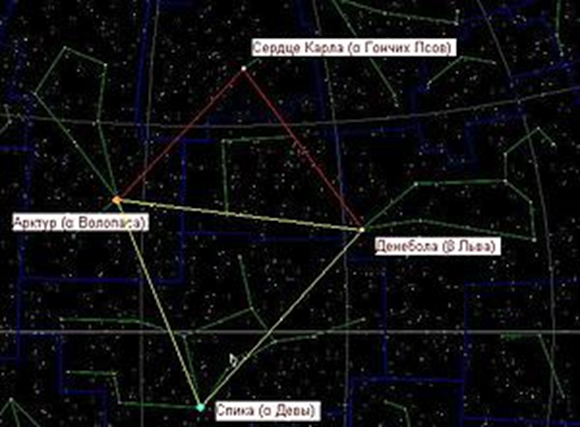
1.8 Треугольники на небе

Треугольники встречаются и в виде созвездий. Весенний треугольник—астеризм в экваториальной части неба. В России лучше всего виден весной. Находится он в экваториальной части неба и состоит из звезд Арктур, Спика и Денебола. Иногда к астеризму добавляется звезда Сердце Карла (α Гончих Псов), дополняющая треугольник до ромба. В этом варианте астеризм известен как Бриллиант Девы.

1.9 Треугольник Петрова

Треугольник Петрова – традиционное русское название приема в эндшпиле в русских шашках. При помощи такого приёма достигается ловля одной

дамки тремя дамками, контролирующих большак. За рубежом этот прием носит название “Способ Монтеро”.

1.10 Знаки дорожного движения

Первые в мире дорожные знаки были утверждены на международной конференции автомобилистов в 1909 году. В числе участников были и представители Российской империи. Дорожных знаков того времени было четыре и все круглой формы: «перекресток», «шлагбаум», «двойной поворот», «препятствие в виде насыпи и канавы». Новые дорожные знаки и сигналы были официально приняты уже в СССР 1 декабря 1927 года. В 1933 году их количество увеличилось до двадцати трёх и они получили привычные сегодня формы и цвет, а также впервые были разделены на три категории: «предупреждающие», «воспрещающие» и «указательные». Следующие изменения и дополнения, касающиеся дорожных знаков, были приняты 1 января 1961 года, после присоединения СССР в 1959 году к Международной конвенции по дорогам и моторному транспорту 1949 года. Число дорожных знаков увеличилось до тридцати шести. Все знаки получили жёлтый фон. В 1968 году в Вене была принята Конвенция о дорожном движении и дорожных знаках и сигналах. Среди стран, принявших Венскую конвенцию, был и СССР. Новые правила дорожного движения, а также дорожные знаки, принятые этой конвенцией, вступили в силу в СССР в 1973 году. В дальнейшем изменения и дополнения в правила дорожного движения, дорожные знаки и сигналы вносились в 1975, 1976, 1979, 1980, 1984 и 1987 годах.

13

1.11 Треугольник Дали

Треугольник Дали — что это?

Многие, столкнувшись с этим понятием, сначала думают, что это какое-то определение в геометрии, но это совсем не так. Треугольник Дали — это общее название трех мест, которые тесно связаны с жизнью знаменитого художника.

Любимый многими испанский художник Сальвадор Дали родился в Фигейрас на севере Каталонии. Многоликий гений, с присущей ему чисто каталонской изменчивостью (столь заметной также у Пикассо и Миро), Дали очень рано проявил себя как человек необычайно живого ума. После учебы в мадридской Академии художеств в 1920-1925 годах, юный Сальвадор вполне мог бы стать глашатаем реализма, но судьба распорядилась по-другому — перепробовав футуризм, кубизм и реализм послевоенного времени, он решил, что ни один из существующих жанров ему не подходит. Увлечение Фрейдом и его анализом подсознательного принесло свои плоды, и Дали серьезно занялся метафизической живописью. Уже в 1929 в галерее Геманс экспонировались его первые сюрреалистические произведения (Загадка желания. Моя мать, моя мать, моя мать, 1929, Цюрих, частное собрание), иллюстрирующие теорию критической паранойи, изложенную в книге «Видимая женщина» (1920). Речь идет о продолжении традиции, берущей свое начало в творчестве Боттичелли, Пьеро ди Козимо, Леонардо да Винчи (который сформулировал ее в своем «Трактате о живописи»). Затем, благодаря ташизму и фроттажам Макса Эрнста, Дали увлекся изображением на холсте образов, вызванных свободными ассоциациями по поводу случайно избранных форм, имеющих какой-либо смысл или нет. 14

Ллорет де Мар

Где, как ни в городе своего детства, великий сюрреалист воплотит мечты о создании собственного театрального музея? О маленьком городке Фигерасе в провинции Жирона вряд ли бы знали даже сами испанцы, если чуть больше века назад там не родился сам Сальвадор Дали. Сейчас этот неприметный городок знает весь мир.

Кадакес

Жизнь Дали неразрывно связана с родиной, здесь он провел большую часть своей жизни. Поэтому, конечно же, столица Каталонии не раз принимала его у себя в гостях. Чтобы познакомиться с работами Сальвадора Дали в Барселоне отправляйтесь в Королевский художественный кружок, который расположился в самом сердце города – в Готическом квартале.

Еще одно старинное здание – спасенное от разрушения Сальвадором Дали. В 1969 году любящий муж дарит своей возлюбленной Гала то, что давно обещал: замок в деревушке Пуболь, который был построен в XI веке. К тому времени замок был в запущенном состоянии, и чета Дали вдохнула в него новую жизнь.

📸 Видео

Виды треугольниковСкачать

Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

ВСЕ ТАЙНЫ БЕРМУДСКОГО ТРЕУГОЛЬНИКА [Топ Сикрет]Скачать

Инопланетяне в треугольнике | Проклятие Бермудского треугольника | DiscoveryСкачать

«Территория заблуждений» с Игорем Прокопенко - выпуск 18 (12.03.2013)Скачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

НИКОЛА ТЕСЛА Раскрывает Жуткую Тайну Египетских Пирамид / Ученые Не Могут Это ОбъяснитьСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Виды треугольниковСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

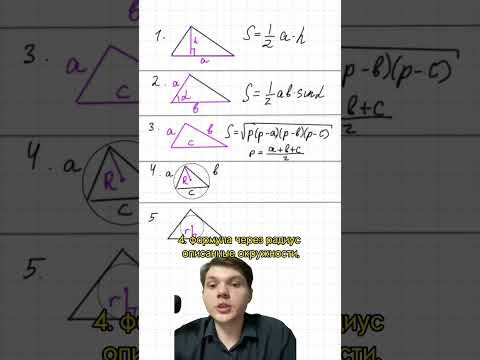
Все формулы площади треугольника #огэ #егэ #shorts #математикаСкачать