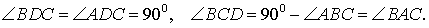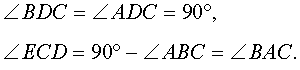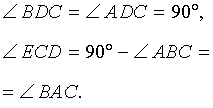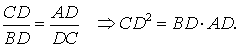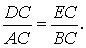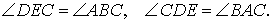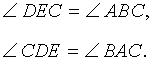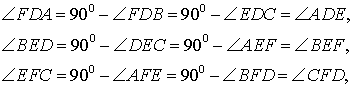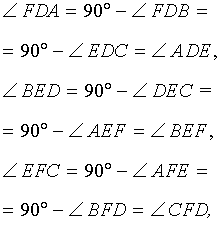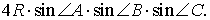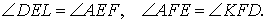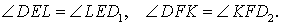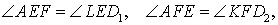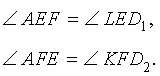- Содержание
- Высота
- Пересечение высот в треугольнике
- Биссектриса
- Медиана
- Решим задачу!
- Высота треугольника
- Высота треугольника. Задача Фаньяно
- Высота треугольника. Свойство высоты прямоугольного треугольника
- Расположение высот у треугольников различных типов
- Ортоцентр треугольника
- Расположение ортоцентров у треугольников различных типов
- Ортоцентрический треугольник
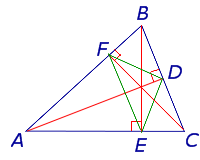
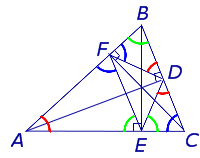
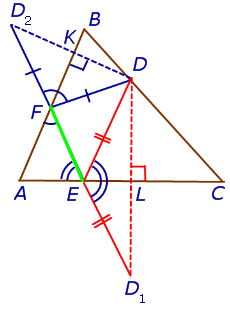
- Задача Фаньяно
- 💡 Видео
Содержание
Из вершин треугольника к противолежащим от вершин сторонам можно проводить различные отрезки, причем так, чтобы получать «интересные данные» внутри фигуры.
К примеру, отрезок из вершины можно опустить таким образом, что в итоге он «приземлится» ровно посередине противолежащей от вершины стороны. В геометрии существует три подобных отрезка, что задают для треугольника новые геометрические параметры — высота, биссектриса и медиана.
Видео:7 класс, 16 урок, Перпендикуляр к прямойСкачать

Высота
Пусть нам дан треугольник $bigtriangleup,$ где из вершины $C$ к противолежащей стороне $AB$ опущен отрезок $CD$, образующий при этом перпендикуляр к стороне $AB$. Тогда отрезок $CD$ будет являться высотой треугольника $bigtriangleup$. Аналогичный перпендикуляр можно опустить как из вершины $A$, так и из вершины $B$.
Высота треугольника — перпендикуляр, проведенный из вершины к прямой, содержащей противолежащую сторону треугольника.
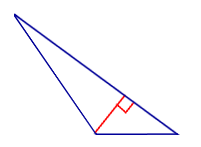
В остроугольном треугольнике — где углы имеют значение $ 90^,$ — провести высоту будет уже не так интуитивно просто.
Осмотрите треугольник $bigtriangleup$ выше, с тупым углом $angle$.
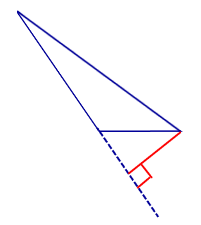
Итак, нам необходимо провести высоту из вершины $K$ к стороне $PM$. Подумайте, как будет располагаться отрезок, выполните чертеж и сравните свои предположения со скрытым чертежом.
Пересечение высот в треугольнике
Выходит, что в остроугольном треугольнике высоты пересекаются в точке, расположенной строго внутри треугольника — никаких дополнительных построений не требуется. Однако в тупоугольном треугольнике высоты пересекаются в точке, расположенной вне треугольника — чтобы эту точку получить, необходимо достраивать продолжение сторон. Так, в случае с нашим тупоугольным треугольником, высоты пересекаются в точке $O$ — внимание на изображение выше.
Видео:Вся геометрия треугольника в одной задаче. Планиметрия. ЕГЭ 2023 математика задача 16Скачать

Биссектриса
Пусть нам дан треугольник $bigtriangleup,$ где из вершины $C$ к противолежащей стороне $AB$ опущен отрезок $CD$ таким образом, что $angle$ делится отрезком $CD$ на два равных друг другу угла. Тогда отрезок $CD$ будет называться биссектрисой треугольника $bigtriangleup$ (от лат. ‘bi’ — «два», ‘secare’ — «резать»).
По аналогии с высотами, такие же отрезки, делящее угол пополам, можно опустить как из вершины $A$, так и из вершины $B$.
Биссектриса треугольника — отрезок, соединяющий вершину с противолежащей стороной и делящий при этом угол данной вершины пополам.
В отличие от высоты, биссектриса — понятие, теснее связанное с углом, чем с треугольником, поэтому ряд ее свойств больше определяет геометрию углов, чем геометрию треугольников. Например, одно из таких замечательных свойств связано со смежными углами. Оказывается, что биссектрисы, проведенные из смежных углов, будут образовывать прямой угол. Давайте это докажем!
Теорема о биссектрисах смежных углов. Биссектрисы смежных углов взаимно перпендикулярны.
Доказательство. $angle$ является смежным с $angle$. $OB$ — биссектриса $angle;$ $OD$, соответственно, биссектриса $angle$. По свойству смежных углов известно, что сумма смежных углов равняется $180^$. То есть:
Согласно условию $angle=angle=frac<angle>$, $angle=angle=frac<angle>$. Тогда уравнение выше можно представить в следующем виде:
Разделим обе части уравнения на $2$ и получим: $angle+angle=90^.$ $angle+angle$ равняется $angle$. Теорема доказана .
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Медиана
Наконец, проведем отрезок $CD$ в треугольнике $bigtriangleup$ из вершины $C$ к противолежащей стороне $AB$ таким образом, что сторона $AB$ поделится на два равных друг другу отрезка. Мы получили третий важный отрезок в треугольнике — медиану (от лат. ‘medianus’ — «средний»).
Медиана треугольника — отрезок, соединяющий вершину с серединой противолежащей стороны.
Медианы, как и биссектрисы с высотами, пересекаются в одной точке внутри треугольника. Исключением является тупоугольный треугольник и его высоты: они пересекаются вне треугольника.
Доказать это, к сожалению, нам пока не по силам, ибо требуется знание нескольких важных теорем, которые мы обязательно изучим в курсе далее. Как только — так сразу. Пока — принять, понять, поверить.
Видео:Окружность. 7 класс.Скачать

Решим задачу!
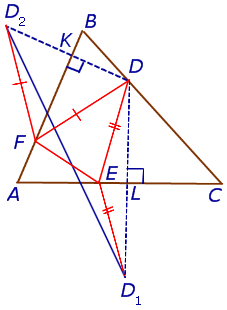
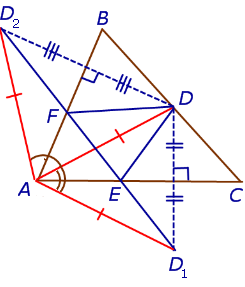
В $bigtriangleup$ проведена медиана $AD$ к стороне $BC$. Продолжение медианы проходит через точку $E$, расположенную вне треугольника так, что $AD=DE$. Докажите, что треугольники $bigtriangleup$ и $bigtriangleup$ равны.
Дано:
Найти:
Решение . Рассмотрим $bigtriangleup$ и $bigtriangleup$. В них углы $angle$ и $angle$ равны как вертикальные. По заданному условию $AD=DE$. Также имеем равенство сторон $CD=DB$ — по определению медианы: отрезка, делящего противолежащую от угла сторону на два равных отрезка.
Следовательно $bigtriangleup= bigtriangleup$ по первому признаку равенства треугольников: двум сторонам и углу, лежащему между ними.
Видео:Задача, которую боятсяСкачать

Высота треугольника
В отличие от медианы или биссектрисы, высота треугольника может быть расположена как внутри треугольника, так и вне его.
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.
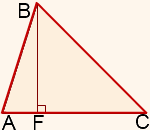
На рисунке BF — высота, проведенная из вершины B к стороне AC.
Все три высоты треугольника пересекаются в одной точке. Эта точка называется ортоцентром треугольника.
Высоты остроугольного треугольника расположены строго внутри треугольника.
Соответственно, точка пересечения высот также находится внутри треугольника.
В прямоугольном треугольнике две высоты совпадают со сторонами. (Это высоты, проведенные из вершин острых углов к катетам).
Высота, проведенная к гипотенузе, лежит внутри треугольника (позднее рассмотрим ее свойства).
AC — высота, проведенная из вершины С к стороне AB.
AB — высота, проведенная из вершины B к стороне AC.
AK — высота, проведенная из вершины прямого угла А к гипотенузе ВС.
Высоты прямоугольного треугольника пересекаются в вершине прямого угла (А — ортоцентр).
В тупоугольном треугольника внутри треугольника лежит только одна высота — та, которая проведена из вершины тупого угла.
Две другие высоты лежат вне треугольника и опущены к продолжению сторон треугольника.

BF — высота, проведенная к продолжению стороны АС.
CD — высота, проведенная к продолжению стороны AB.
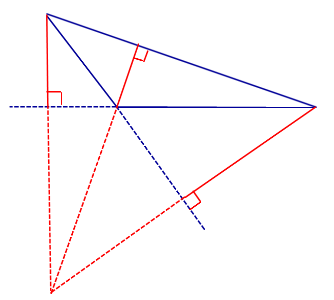
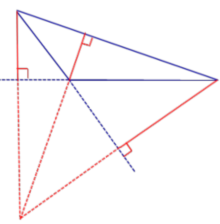
Точка пересечения высот тупоугольного треугольника также находится вне треугольника:
Видео:№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

Высота треугольника. Задача Фаньяно
 Высота треугольника. Свойство высоты прямоугольного треугольника Высота треугольника. Свойство высоты прямоугольного треугольника |
 Расположение высот у треугольников различных типов Расположение высот у треугольников различных типов |
 Ортоцентр треугольника Ортоцентр треугольника |
 Расположение ортоцентров у треугольников различных типов Расположение ортоцентров у треугольников различных типов |
 Ортоцентрический треугольник Ортоцентрический треугольник |
 Задача Фаньяно Задача Фаньяно |
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Высота треугольника. Свойство высоты прямоугольного треугольника
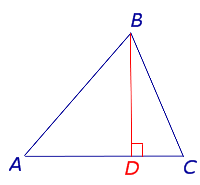
Определение 1 . Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
На рисунке 1 изображена высота BD , проведённая из вершины B треугольника ABC . Точка D – основание высоты.
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
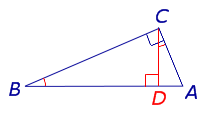
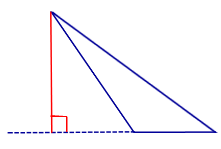
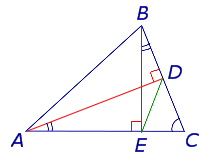
Утверждение . Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).
Доказательство . Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям
Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD , что и требовалось доказать.
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
Видео:Где находится точка в треугольнике заданном координатами вершин, внутри или вне треугольника.Скачать

Расположение высот у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | 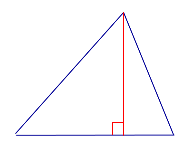 | Все высоты остроугольного треугольника лежат внутри треугольника. |
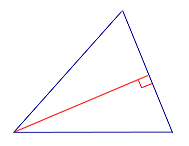 | ||
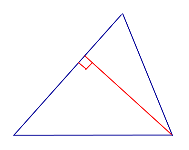 | ||
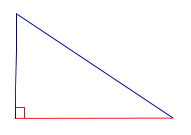
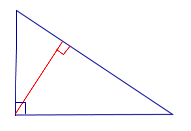
| Прямоугольный треугольник | 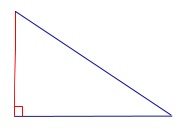 | Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника |
 | ||
 | ||
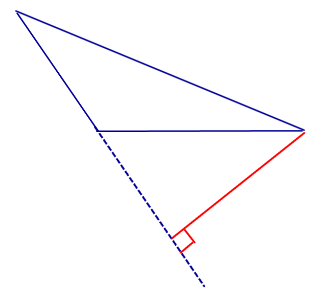
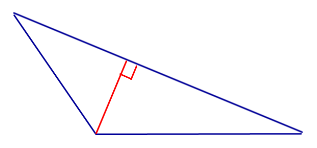
| Тупоугольный треугольник | 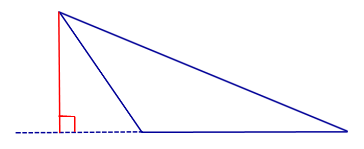 | Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
 | ||
 |
| Остроугольный треугольник | ||
 |  |  |
| Все высоты остроугольного треугольника лежат внутри треугольника. | ||
| Прямоугольный треугольник | ||
 |  |  |
| Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника | ||
| Тупоугольный треугольник | ||
 |  |  |
| Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника | ||
Все высоты остроугольного треугольника лежат внутри треугольника.
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника
Видео:Из-за этого женщина мгновенно теряет интерес к мужчине!Скачать

Ортоцентр треугольника
Теорема 1 . Высоты треугольника (или их продолжения) пересекаются в одной точке.
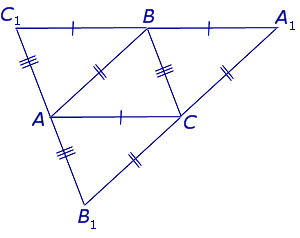
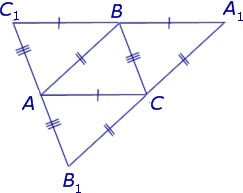
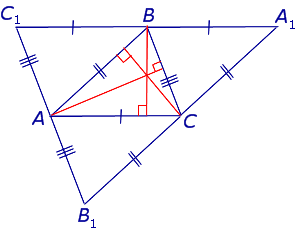
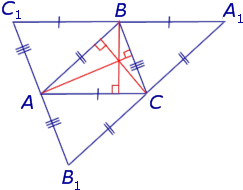
Доказательство . Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).
Обозначим точки пересечения этих прямых символами A1 , B1 и C1 , как показано на рисунке 3.
Следовательно, точка B является серединой стороны C1A1 .
Следовательно, точка A является серединой стороны C1B1 .
Следовательно, точка C является серединой стороны B1A1 .
и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.
Теорема 1 доказана.
Определение 2 . Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.
Видео:№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать
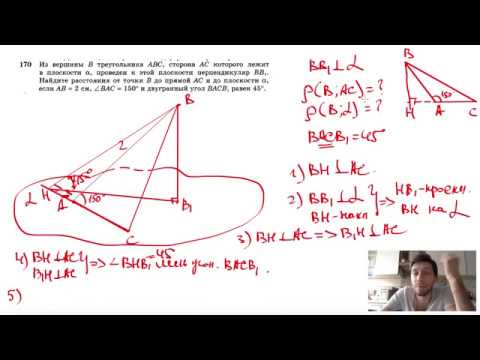
Расположение ортоцентров у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | 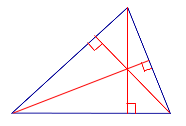 | |
| Прямоугольный треугольник | 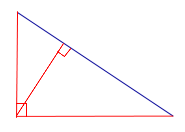 |